Matematični modeli širjenja epidemije

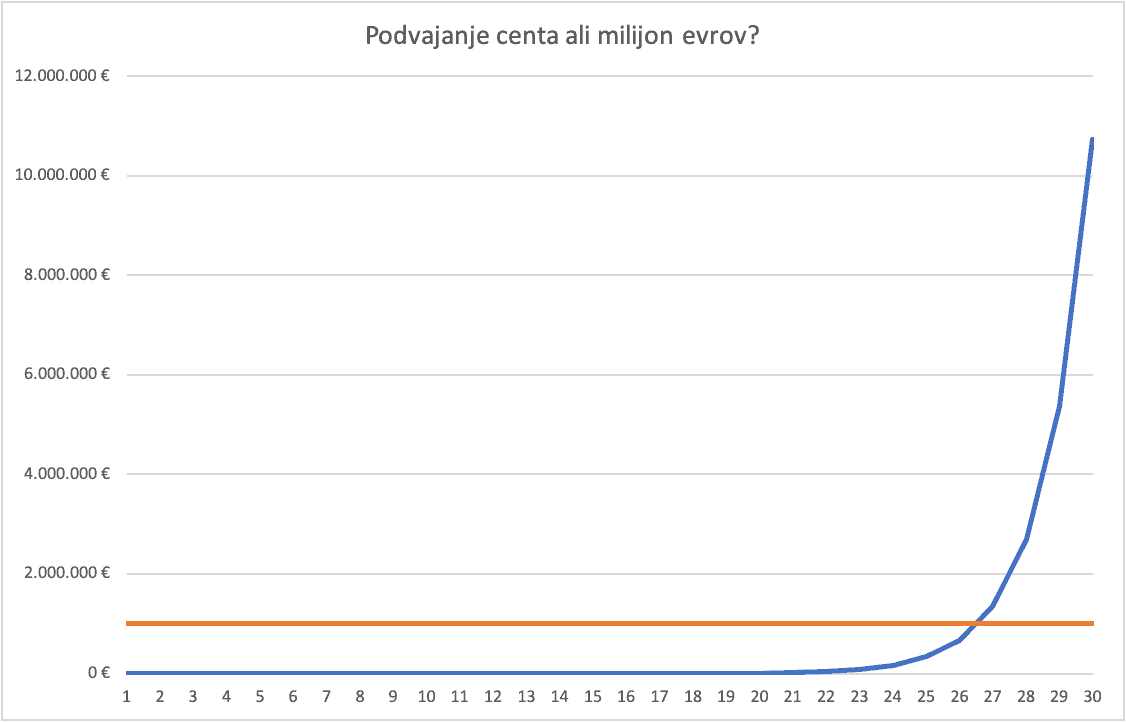
Za kaj bi se odločili, če bi vam nekdo ponudil možnost izbire med milijonom evrov takoj in tridesetimi zaporednimi dnevi nakazil, ki bi se začela z enim samim centom, nato pa bi se vsak dan podvojila? Vsi, ki ste vešči matematike, boste znali hitro izračunati, da se bolj splača izbrati zaporedje nakazil, saj boste imeli tako na koncu več kot desetkrat večjo skupno vsoto, kot če bi se odločili za milijon.

Vendar izbira zaporedja nikakor ni očitna in vsakomur razvidna. Zdrava pamet oziroma odločanje po občutku nam v tem primeru ne svetuje, da je bolje izbrati zaporedje. Da se kar najbolj smotrno odločimo, si moramo pomagati z matematičnim izračunom, za kar pa potrebujemo nekaj predznanja.

Za eksponentno rast nimamo intuitivnega občutka

Zadnje čase se človeštvo pogosto sooča z dilemami, pri katerih najboljša dolgoročna izbira ni očitna na prvi pogled. Če pogledamo skozi okno, učinka podnebnih sprememb ne moremo neposredno zaznati. Šele, ko vremenske podatke za daljše obdobje podrobno analiziramo, lahko opazimo trende njihovega dolgoročnega spreminjanja, prave vzroke za spremembe pa lahko ugotovimo šele z računalniškimi simulacijami.

Podobno je z epidemijo covid-19, pri kateri imamo sicer osnovni uvid v naraščanje okuženosti populacije preko števila vsakodnevno novih pozitivnih na testih, vendar si lahko tudi v tem primeru pravo predstavo o stanju in razsežnosti epidemije ustvarimo šele z natančno analizo podatkov.

Najbolj preprost matematični model, ki dobro opiše začetne faze širjenja nalezljive bolezni, je podoben rasti kupčka denarja, kot smo ga opisali z zaporedjem nakazil, ki se vsak dan podvojijo. Če bi vsak okuženi vsak dan okužbo prenesel še na dve osebi, bi primeri dejansko naraščali po enaki krivulji, kot se kopiči denar na našem računu.

Pri eksponentni rasti lahko pride do dramatičnih sprememb zelo hitro, zato se jim je dobro vnaprej izogniti. Ko se enkrat zgodijo, je namreč izjemno težko ukrepati. A ker naši možgani niso pogosto soočeni z eksponentno rastjo, za takšna zaporedja nimamo intuitivnega občutka. Marsikdo se recimo sprašuje, kako to, da osebno ne pozna nikogar, ki je okužen z novim koronavirusom? Takšno vprašanje lahko primerjamo s situacijo, če bi se sredi meseca, nekje po polovici prejetih nakazil, jezili, zakaj nismo raje kot zaporedja nakazil izbrali milijona evrov.

Tipičen primer eksponentne rasti je razmnoževanje bakterij v gojišču, kjer se njihovo število podvoji na enoto časa, dokler mikroorganizmom ne zmanjka hranil. Podobno kot pri naraščanju števila bakterij, eksponentna rast dobro opiše dogajanje med začetno fazo epidemije, za opis nadaljnjega razvoja okužbe v populaciji pa moramo uporabiti drugačna orodja.

Prvi matematični modeli širjenja bolezni

Enega prvih, malo bolj zapletenih matematičnih modelov širjenja nalezljive bolezni, je okoli leta 1910 izdelal angleški zdravnik Ronald Ross. Leta 1902 je dobil Nobelovo nagrado za medicino za spoznanje, da so za prenašanje malarije odgovorni komarji. Žal pa mu ni uspelo prodreti z idejo, da je treba za eliminacijo malarije začeti načrtno uničevati gnezdišča komarjev.

Šele, ko je s pomočjo matematičnega modela pokazal, da za omejitev širjenja malarije komarjev ni treba povsem iztrebiti, ampak je dovolj, da njihovo populacijo ustrezno zmanjšamo, so njegove nasvete začeli bolj resno obravnavati.

Ob epidemijah kolere in podobnih nalezljivih boleznih učenjaki dolgo časa tudi niso znali pojasniti, zakaj enako hitro, kot se izbruhi pojavijo, nato tudi minejo. Med obema svetovnima vojnama so zato razvili nov matematični model za opis širjenja epidemije, ki v najbolj preprosti verziji populacijo razdeli na tri dele: na dovzetne za okužbo, na okužene in na tiste, ki se ne morejo več okužiti. Danes ga imenujejo SIR model po začetnih črkah angleških besed za posamezne podskupine (susceptible, infectious, removed).

Bistveno pri takšnem modelu je, da lahko zanj zapišemo enačbe, ki opisujejo prehajanje ljudi med posameznimi fazami okužbe in bolezni. SIR model lahko poenostavljeno razumemo kot pretakanje tekočine med posodami, ki predstavljajo osebe v različnih fazah okužbe. Z modelom lahko izračunamo, kako se spreminja število okuženih s časom glede na nalezljivost bolezni, za posamezne parametre bolezni pa lahko predvidimo tudi, koliko ljudi bo med epidemijo zbolelo, kakšen bo največji delež okuženih, kolikšen mora biti delež cepljenih, da dosežemo čredno imunost in podobne podatke, ki so pomembni za načrtovanje odziva na epidemijo.

Reprodukcijsko število

Eden od ključnih parametrov v matematičnih modelih epidemije je reprodukcijsko število, ki ga označimo z R, predstavlja pa stopnjo nalezljivosti neke kužne bolezni. Osnovno reprodukcijsko število R₀ je opredeljeno kot povprečno število ljudi, ki jih ena kužna oseba okuži v času svoje kužnosti v populaciji, v kateri so vsi posamezniki dovzetni za okužbo.

Najbolj kužne nalezljive bolezni so ošpice, norice, rdečke in mumps. Pri ošpicah lahko en okuženi v povprečju okuži tudi več kot 10 necepljenih ljudi, kar pomeni, da se takšna okužba širi bliskovito. Prav zato je za preprečevanje izbruhov najbolj nalezljivih bolezni ključna dobra precepljenost populacije. S tem namreč bistveno zmanjšamo dejansko reprodukcijsko število bolezni.

Na splošno velja, da je epidemija v razmahu, ko je R večji kot 1, kar praviloma ustreza zgodnjim fazam epidemije, ko število okuženih narašča eksponentno. Ko R pade pod 1, se širjenje nalezljive bolezni upočasnjuje, saj vsak okuženi bolezen prenese na manj kot eno osebo.

Težava z reprodukcijskim številom pa je, da ne zaobjame razpršenosti posameznih primerov širjenja okužbe, kar je še posebej značilno za virus SARS-Cov-2. Kot kažejo analize, pri tem virusu vsi kužni ne prenesejo okužbe naprej z enako intenziteto, ampak se virus občasno množično razširi preko dogodkov superširjenja. Trenutno velja ocena, da je za kar 80% prenosov okužb odgovornih le 20% okuženih.

Računalniške simulacije epidemije

Z računalnikom lahko simuliramo širjenja okužbe v populaciji tudi na podoben način, kot to počnejo nekatere računalniške igrice. Za Slovenijo lahko tako v model vnesemo dva milijona virtualnih prebivalcev, ki jim glede na statistične podatke pripišemo lastnosti kot so starost, velikost gospodinjstva, družabnost, mobilnost, dovzetnost za okužbo in podobno.

Nato poženemo simulacijo, pri kateri po korakih izračunavamo, kako se virus širi med ljudmi. Zelo poenostavimo rečeno deluje simulacija tako, da računalnik za vsak stik okuženega ustvari naključno število med 0 in 100. Če model predvidi, da je verjetnost za prenos okužbe recimo 20%, računalnik zabeleži uspešen prenos okužbe, če je naključno število manjše od 20, sicer pa smatra, da do prenosa okužbe ni prišlo.

Tako simulacijo nato velikokrat ponovimo z rahlo spremenjenimi začetnimi pogoji in parametri, ki opisujejo lastnosti širjenje koronavirusa in potek bolezni pri posameznih skupinah prebivalcev. Iz mnogih ponovitev simulacije lahko pripravimo verjetnostno napoved, ki napove, kako se bo epidemija najverjetneje razvijala pod danimi pogoji. Na ta način lahko s spremembo parametrov primerjamo tudi, kako bo posamezen ukrep vplival na širjenje bolezni. Lahko recimo nastavimo, da le 75% ljudi dejansko uporablja maske, da je prepovedano zbiranje v večje skupine ali zapuščanje bližine prebivališča.

Vendar pa simulacij in modeliranja ne smemo zamenjevati s preprosto ekstrapolacijo podatkov. Če poskušamo iz vsakodnevno objavljenih podatkov le predvideti, kakšen bo trend gibanja nekega parametra naslednje dni, potem praviloma (še) nismo postavili matematičnega modela pojava. Za izgradnjo resne matematične simulacije moramo poznati dejanske matematične zakonitosti, ki veljajo za pojav. Šele z njihovo pomočjo lahko zgradimo ustrezen matematični opis pojava, ki mu lahko zaupamo.

Zelo pomembno je tudi, da model preizkusimo na že znanih podatkih. Šele v primeru, ko matematična simulacija pravilno napove razvoj obravnavanega pojava v preteklosti, je smiselno govoriti o kakršni koli napovedni vrednosti modela za prihodnost.

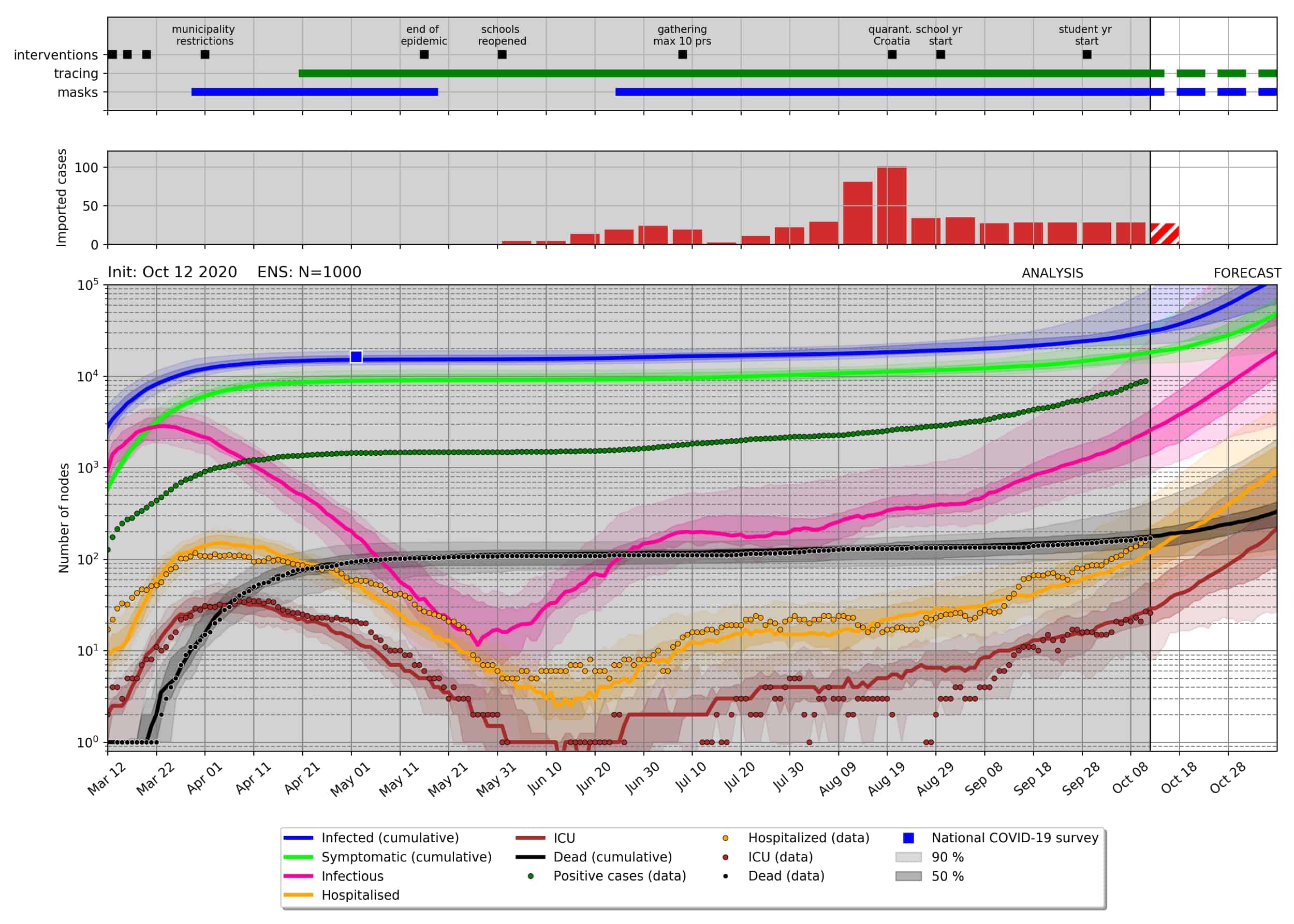
Dodano 12.10.2020: V dogovoru z Žigo Zaplotnikom s Fakultete za matematiko in fiziko Univerze v Ljubljani objavljamo verjetnostno napoved poteka epidemije v Sloveniji, ki je bila narejena ob predpostavki, da se naše vedenje ne bi spremenilo tudi potem, ko je bila 6. 10. 2020 presežena kapaciteta, do katere lahko epidemiologi še obdelajo in poiščejo vse kontakte potrjeno okuženih. Kot lahko vidite na grafu, začne število okuženih pod temi pogoji zelo hitro naraščati. Zato je sedaj res pomembno, da vsi omejimo svoje ne-nujne stike, če se le da delamo od doma, striktno nosimo masko in se držimo priporočil. Prav tako je zelo priporočeno, da si naložite aplikacijo #OstaniZdrav, če imate le ustrezen telefon. Sedaj je bilo tudi pri nas že na več primerih neposredno potrjeno, da aplikacija dejansko pomaga pri obveščanju o rizičnih stikih, vanjo pa je bilo do sedaj naloženih že več kot tri tisoč dnevnih ključev okuženih.

Dodatno branje:

• Andrej Srakar: Uvod v modeliranje in statistične vidike COVID-19 | Udomačena statistika
• Aleš Mohorič: Deterministični model epidemije, Obzornik za matematiko in fiziko, 66 (2019) 6.
• Zaplotnik Ž, Gavrić A, Medic L (2020) Simulation of the COVID-19 epidemic on the social network of Slovenia: Estimating the intrinsic forecast uncertainty. PLOS ONE 15(8): e0238090. https://doi.org/10.1371/journal.pone.0238090
• COVID-19 Sledilnik – Modeli in napovedi

-