Paradoks dvojčkov

Najprej si oglejmo paradoks dvojčkov v osnovni obliki v okviru posebne teorije relativnosti (torej v okviru teorije, ki ne vključuje vpliva gravitacije). Zapis najdemo v članku Uvod v posebno teorijo relativnosti:

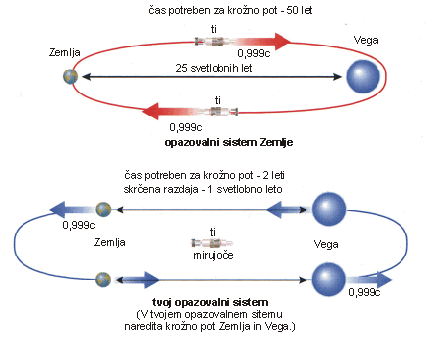
…Miselni poskus 13: Zamisli si, da bi šel na pot do zvezde Vega, ki je oddaljena 25 svetlobnih let. Na voljo imaš ladjo, ki lahko potuje s hitrostjo 0,999c. Potovanje bi za opazovalca na Zemlji trajalo približno 25 let, saj potuješ skorajda s svetlobno hitrostjo, razdalja pa je 25 svetlobnih let, in prav toliko še za vrnitev. Če odpotuješ recimo leta 2025, bi Vego dosegel leta 2050, na Zemljo pa bi se vrnil leta 2075. Iz tvojega opazovalnega sistema pa se ti zdi, da ostajaš na mestu, s hitrostjo 0,999c pa se oddaljuje Zemlja in približuje Vega. Zato se ti bo razdalja med Zemljo in Vego iz 25 svetlobnih let skrčila na nekaj več kot 1 svetlobno leto. Ker se ti Vega približuje s hitrostjo 0,999c, razdalja do Vege pa je zate le 1 svetlobno leto, bo potovanje do Vege zate trajalo le 1 leto. Nazaj boš prav tako potoval le eno leto, zato bodo tvoje ure izmerile za celotno pot le 2 leti. Če boš ob odhodu star 30 let, se boš vrnil star 32 let. Čeprav se zdijo naše ugotovitve nenavadne, sta oba pogleda na potovanje prava. Če odpotuješ z Zemlje leta 2025, ko si star 30 let, se boš vrnil leta 2075, ko boš star 32 let. Čeprav se boš med potjo postaral le za 2 leti, bodo tvoji prijatelji na Zemlji ob povratku starejši kar za 50 let.

Načrtoval pa bi lahko tudi daljše polete na bolj oddaljene zvezde v vesolju, če bi le imel dovolj hitro ladjo. Andromedina galaksija je oddaljena 2,5 milijonov svetlobnih let, kar pomeni, da bi pot do nje in nazaj za opazovalca na Zemlji trajala 5 milijonov let. Vendar pa bi, če bi le uspel potovati s hitrostjo, ki je že zelo blizu svetlobni hitrosti [ npr. (1-5*10-11)c ], bi zate celotno potovanje trajalo le 50 let. Če bi Zemljo zapustil za svoj 30-ti rojstni dan, se bi vrnil star 80 let, pri čemer bi ob povratku našel le še ostanke našega sončnega sistema, vsi prijatelji in vse kar ti je bilo znano, pa bi izginilo že pred 5 milijoni let …

Razrešitev gornjega paradoksa najdemo v članku o splošni teoriji relativnosti , to je o sestavku o teoriji, ki vključuje tudi gravitacijo in pospešeno gibanje:

…. Razrešitev paradoksa dvojčkov
Zamisli si dvojčka, od katerih eden ostane na Zemlji, drugi pa se poda na pot z zelo hitro raketo do bližnje zvezde in nazaj. V miselnem poskusu 13 (glej članek o posebni teoriji relativnosti) smo napovedali, da se bo dvojček, ki je potoval po vesolju, manj postaral, kot njegov brat, ki je ostal na Zemlji. Kaj ne bi lahko z istimi argumenti tudi potujoči brat trdil, da je pravzaprav on miroval, na popotovanje stran in nazaj glede nanj pa se je odpravila Zemlja z drugim bratom na njej? Kaj ne bi moral biti po tej logiki brat na Zemlji tisti, ki se je manj postaral? Z vprašanjema smo odprli t. i. paradoks dvojčkov. Poskušajmo ga razrešiti!
Zamisli si, da lebdita skupaj s Tino v breztežnosti vsak v svoji vesoljski ladji eden ob drugemu in sinhronizirata svoje ure. Medtem ko ti ostaneš v breztežnosti, Tina vklopi na svoji ladji motorje in se pospešeno odpelje malo stran, nato pa z vzvratnimi motorji zavre in se ustavi. Potem se obrne in na enak način vrne na mesto ob tebi od koder se je podala na pot. Iz tvojega opazovalnega sistema vidiš, da Tinine ure bijejo počasneje kot tvoje. Ob njenem povratku tako pričakuješ, da je zanjo poteklo manj časa, kot zate. In kako vidi dogajanje Tina? Ali vidi tudi ona dogajanje natanko tako kot ti?
S Tino se lahko neskončno časa prepirata, kdo se zares giblje, vendar se okoli nečesa vseeno morata strinjati: med popotovanjem si ti ostal v breztežnosti, medtem ko je Tina ob pospeševanju čutila težo, ki jo je pritisnila k tlom njene vesoljske ladje. Tina si lahko svojo težo razlaga na dva različna načina. Lahko se strinja s tabo, da je bila ona tista, katere ladja se je pospeševala. Ker pa vemo, da teče čas počasneje v pospešeni vesoljski ladji, se bo tako Tina morala strinjati, da so njene ure tekle počasneje kot tvoje. Lahko pa ubere drugačno pot in trdi, da je čutila težo zato, ker so se morali motorji na njeni ladji upirati gravitacijskemu polju, v katerem je bila pri miru, medtem ko si ti v njem prosto padal. Ker pa vemo, da teče čas v gravitacijskem polju počasneje, se mora tudi v tem primeru s Tino strinjati, da tečejo njene ure počasneje od tvojih. Ne glede na to, kako s Tino interpretirata dogajanje, je rezultat enak: za Tino poteče med popotovanjem manj časa….

Sedaj pa k vprašanju samemu. V prvi postavitvi paradoksa dvojčkov (potovanje z Zemlje na Vego) je bila gravitacija zanemarjena, Zemlja je bila tu uporabljena le kot referenčna točka v prostoru, nikakor pa ne kot masivno telo, ki ga obdaja gravitacijsko polje (ali v jeziku splošne teorije relativnosti, ki ukrivlja prostor čas okoli sebe). Bolje se je torej lotiti druge postavitve paradoksa dvojčkov s teboj in Tino, saj je tam jezik nekoliko bolj natančen.

Najprej se spomnimo, da se v članku o splošni teoriji relativnosti oba (ti in Tina) nahajata v breztežnem prostoru. Paradoks dvojčkov je le navidezen, ker oba, Tina in ti, nista v enakovrednem položaju. Trditev posebne teorije relativnosti je, da so vsi inercialni sistemi (sistemi, ki se gibljejo enakomerno) enakovredni. Če se torej Tina giblje enakomerno glede na tebe, opazi, da njej teče čas hitreje kot tebi, medtem ko ti opaziš, da tebi ura teče hitreje kot njej. Vendar Tina s pospeševanjem preskakuje iz enega v drugi inercialni sistem (hitrost se ji spreminja). Tako Tina in ti nista v enakovrednem položaju. Tina pospešuje, ti pa ne. Pri tem lahko tudi ugotovita, kdo se nahaja v neinercialnem sistemu (takem, ki pospešuje)! Le interpretacija je stvar dogovora. Tina namreč ob pospeševanju čuti silo, ki jo lahko pripiše pospeševanju, ravno tako legitimno pa si lahko zamisli tudi gravitacijsko polje, ki povzroča enako silo. Ti ne čutiš nobene sile (ne pozabimo, še vedno smo v vesolju, ne na Zemlji), kar lahko interpretiraš kot dejstvo, da si v inercialnem sistemu, ali pa si zamisliš gravitacijsko polje, v katerem pospešeno padaš s težnim pospeškom, tako da ne čutiš sile teže (kot npr. v padajočem dvigalu). V obeh primerih je neizpodbitno, da ti ne čutiš sile, Tina pa jo. In Tina bo čutila ob pospeševanju silo, ne glede na to, kako hitro bo pospešila. Če pospeši trenutkoma, bi čutila sistemsko silo sicer le tisti trenutek, kasneje pa ne. Seveda bi bila v tem primeru sistemska sila izredno velika (in bi Tino verjetno tudi poškodovala). Vsekakor pa brez sistemske sile pri pospeševanju ne gre…

Sedaj vključimo v igro še Zemeljsko gravitacijsko polje, ki stvari dodatno zaplete. Naj torej ti in Tina na začetku mirujeta na Zemlji. Nato se Tina z raketo izstreli v vesolje. Kako hitro teče Tini čas glede na tvojega določata dve stvari, relativna hitrost (glede na Zemljo) in kje se nahaja v gravitacijskem polju. Ure, ki so v gravitacijskem polju postavljene “višje” (na večjem gravitacijskem potencialu) tečejo hitreje. Tako ure v gorah tečejo hitreje kot ob morju. Vendar pa se Tinina ura (in z njo Tina seveda) tudi giblje glede na tvoj sistem (glede na površje Zemlje). Napoved posebne teorije relativnosti pa je, da gibajočo uro v mirujočem sistemu vidimo, kot da teče počasneje. Naj povzamem: ker se Tina premika stran od Zemljinega površja, je v gravitacijskem polju vse višje: ura teče vse hitreje, ker pa se premika mora teči vse počasneje (oboje seveda zapisano s stališča opazovalca na površju Zemlje). Od relativne velikosti obeh prispevkov je tako odvisno ali bo Tinina ura tekla hitreje ali počasneje. Če bo na primer planinec, katerega hitrost hoje je precej manjša od ubežne hitrosti z Zemlje 11km/s, odnesel atomsko uro na vrh Triglava in jo tam pustil leto ali dve, ter jo nato odnesel nazaj, bo opazil, da je ura tekla hitreje kot referenčna ura v Piranu. Povsem drugače pa je, če se Tina z raketo, s katero dovolj hitro doseže (ali preseže) ubežno hitrost, odpravi v vesolje, se nato po letu ali dveh obrne in vrne nazaj na Zemljo. Tedaj bi opazili, da je Tinina ura tekla počasneje kot referenčna ura na Zemlji.

Za posvečene zapišimo še rezultat računa

kjer je čas, kot ga izmeri Tina (njen lastni čas), v(t) je hitrost, ki jo ima Tina ob času t, kjer je t čas kot ga izmeri opazovalec v vesolju (v breztežnosti), pa je gravitacijski potencial na mestu x(t). Za krogelno telo je ta

kjer je M masa telesa (v našem primeru Zemlje), G gravitacijska konstanta in r oddaljenost od središča Zemlje. Integracija teče od začetnega časa, ko Tina odleti z Zemlje, do časa, ko se vrne. Čas, ki ga izmeri opazovalec na površju Zemlje dobimo z isto enačbo, le da je hitrost v=0, x(t) pa je vedno ista točka na površju Zemlje.

Nadaljnje branje:
Uvod v posebno teorijo relativnosti
Uvod v splošno teorijo relativnosti
Še en zapis o paradoksu dvojčkov

(Jure Zupan)

-