|
Ali obstaja tudi četrta generacija kvarkov? Ali obstaja kakšna omejitev za največjo mogočo maso kvarkov? Je mogoče, da bodo nekoč odkrili še četrto, peto, … generacijo kvarkov (morda celo neskončno, če bi imeli na voljo neskončno energije za tvorbo novih delcev) in tako ne bomo ostali “le” pri šestih kvarkih razporejenih v tri generacije? Ali je mogoče, da bodo kdaj iz težjih kvarkov in pripadajočih leptonov “sestavili” zelo zelo težke atome (elemente). |
| Osnovni delci | |||
| KVARKI | LEPTONI | ||
| okus | naboj(e0) | delec | naboj(e0) |
| u | 2/3 | e– | -1 |
| d | -1/3 | 0 | |
| c | 2/3 | -1 | |
| s | -1/3 | 0 | |
| t | 2/3 | -1 | |
| b | -1/3 | 0 | |
S svojim vprašanjem si načel eno pomembnejših vprašanj sodobne fizike osnovnih delcev, ki pa je vsaj deloma že odgovorjeno. V Standardnem modelu osnovnih delcev in interakcij namreč nastopa šest kvarkov, in šest leptonov, kot jih kaže zgornja tabela. Le ti so razdeljeni v tri skupine, tako imenovane generacije, saj je vsaka skupina pravzaprav le kopija prejšnje. V vsakdanjem svetu srečamo kvarke in leptone iz prve generacije, saj kvarka u (up) in d (down) sestavljata na primer proton (uud) in nevtron (udd), leptona iz prve generacije pa sta elektron in elektronski nevtrino. Naslednji dve generaciji nato vsebujejo zopet po štiri delce, to je po dva kvarka in po dva leptona, ki so po svojih lastnostih precej podobni kvarkom in leptonom iz prve generacije, a med njimi obstajajo seveda tudi pomembne razlike. Tako so delci iz druge in tretje generacije nestabilni, razpadajo v delce iz prve generacije, poleg tega pa so delci iz vsake naslednje generacije tudi mnogo bolj masivni kot delci iz prejšnje. Povedano povzema spodnja tabela, kjer so delci posameznih generacij označeni z istimi barvami, poleg pa so zapisane še mase (v fiziki visokih energij je običajna enota za energijo 1eV, to je energija, ki jo pridobi elektron, ko preleti napetost enega volta, še bolj prikladna enota pa je GeV=109 eV. Prek slavne Einsteinove enačbe lahko z enotami za energijo izrazimo tudi maso, saj je E=mc2. Masa je tako zapisana v enotah 1GeV/c^2=1.78 10-27 kg.)
|
|
|
Prvo kar opazimo je, da se masa kvarkov dramatično povečuje, ko gremo iz prve generacije v drugo in v tretjo. Masa t kvarka je tako kar okoli 3600-krat večja od mase najlažjega kvarka, t.j. u-kvarka. Še toliko večje so razlike, če primerjamo mase kvarkov tudi z masami leptonov. Masa najtežjega osnovnega delca, t kvarka, je namreč vsaj 100 milijardkrat večja od mase elektronskega nevtrina (da imajo le ti maso različno od nič kažejo eksperimenti zadnjih let, o čemer smo tudi pisali na straneh Kvarkadabre ). Gre torej za velikanska razmerja, katerih izvor ostaja skrivnost sodobne fizike. Dejstvo, da je vsaka generacija osnovnih delcev težja od prejšnje, pa nas kar samo pripelje na misel, da morda obstaja še četrta, peta, itd. generacija osnovnih delcev, ki bi bila ravno tako le kopija prve, a z masami veliko večjimi od mas delcev prve generacije. Tako velikimi masami pač, da delcev višjih generacij pri sodobnih eksperimentih na trkalnikih še ne bi proizvedli in jih kot takih tudi ne bi opazili.
Na srečo obstaja nekaj posrednih dokazov, ki nakazujejo, da ali četrte generacije sploh ni, ali pa je resnično težka. Prvi eksperiment, ki je osvetlil morebitno število generacij so opravili na trkalniku LEP v CERN-u, Ženeva, kjer so sodelovali tudi Slovenski znanstveniki z Instituta Jožef Stefan. Pri eksperimentih na LEP-u so trkali elektrone in pozitrone pri tako velikih energijah, da so nastajali nosilci nevtralnih tokov šibke interakcije, tako imenovani umeritveni bozoni Z. Ti nato razpadajo v par kvark-antikvark, lahko pa tudi lepton-antilepton. Tako lahko kot končni produkt nastane tudi par nevtrino-antinevtrino. Ker nevtrino in antinevtrino zelo, zelo šibko reagirata s snovjo (večina nevtrinov preleti Zemljo ne da bi reagirala) odletijo iz detektorja ne da bi jih zaznali. Dogodek v detektorju tako izgleda kot: trčita elektron in pozitron, nastane bozon Z, ki hipoma (tako hitro, da njegove sledi v detektorju ne zaznamo) razpade, in puf, naenkrat ne zaznavamo ničesar več, saj nevtrino in antinevtrino pobegneta iz detektorja, ne da bi pustila sledi. Če preštejemo tovrstne dogodke elektron-pozitron v “nič” lahko od tu preberemo število različnih generacij nevtrinov.
Na spodnjem grafu so zbrani podatki za verjetnost anihilacije elektron-pozitron v bližini resonance Z (produkcije umeritvenih Z bozonov). Eksperimentalni podatki so pike, črte pa kažejo teoretično napoved za primer 2, 3, 4 generacij. Vidimo, da se teoretična napoved za primer treh generacij nevtrinov odlično prilega eksperimentu, ostale možnosti pa so izključene.
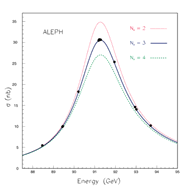
Na kaj lahko od tu sklepamo? Vsekakor ni četrte generacije, ki bi imela nevtrine lažje od približno 45 GeV/c^2 (to je od polovice mase Z bozona, za produkcijo dveh delcev mase m, pač rabimo 2mc^2 energije). Če za četrto generacijo velja podobna hierarhija mas kot za prve tri, tedaj so kvarki četrte generacije izredno težki, več kot miljonkrat težji od najtežjega t kvarka. Tako razmerje med masami bi bilo zelo presenetljivo (ne pozabimo- med znanimi kvarki je največje razmerje mas nekaj tisoč, nikakor ne milijon). Še težje pa bi pojasnili razmerje mas med nevtrini četrte generacije in nevtrini ostalih treh generacij, saj bi bilo to vsaj nekaj deset milijard!
Na število generacij dobimo omejitve tudi iz povsem drugega področja, iz kozmologije. Za nukleosintezo (tvorbo jeder vodika in helija) ob velikem poku je namreč zelo pomembno število lahkih delcev, ki so se nahajali ob času nukleosinteze v “juhi” velikega poka. Število delcev namreč podaja energijo vesolja v danem trenutku, ta pa hitrost razpenjanja. Če je delcev več, je energija večja, hitrost razpenjanja vesolja tudi, zato nukleosinteza traja manj časa, kar pa se nato zopet kaže na razmerju vodika in helija, ki nastane. Iz astronomskih meritev številčnosti helija (pa tudi iz natančnih meritev sevanja mikrovalovnega ozadja, a se raje v tovrstne podrobnosti ne bi spuščali) lahko zopet s precejšnjo gotovostjo trdimo, da je število generacij lahkih nevtrinov enako tri.
Vse torej kaže na to, da so generacije osnovnih delcev le tri, oziroma, da so morebitne dodatne generacije izredno težke in s tem nedosegljive na eksperimentih nove generacije, prvi predstavnik katerih je LHC (tega trenutno gradijo v CERNu in bo predvidoma končan leta 2007). Nikakor pa dejstvo, da so dodatne generacije osnovnih delcev (če le te seveda sploh obstajajo) najverjetneje eksperimentalno nedosegljive v bližnji prihodnosti, ne pomeni, da je s tem konec fizike visokih energij. Odpira se namreč kar nekaj teoretičnih možnosti nadgradnje Standardnega modela osnovnih delcev in interakcij. Najstarejša od njih je veja Velikih teorij poenotenja (GUT-Grand Unified Theories), ki poenotijo elektromagnetno, šibko (ti dve sta poenoteni že v okviru Standardnega modela) in močno interakcijo, vendar pa ob tem vpeljejo tudi nove delce (nove umeritvene bozone in dodatne, tako imenovane Higgsove bozone – v Standardnem modelu je Higgsov bozon le eden). Vendar pa imajo ti delci maso okoli 10 16 GeV. Če to primerjamo na primer z energijo, ki jo je dosegal trkalnik na LEPu, okoli 200 GeV, uvidimo da delcev, ki jih napovejo GUT teorije ne bomo tako kmalu proizvedli na trkalnikih.
Z eksperimentalnega stališča je veliko bolj zanimiva možnost supersimetrije, to je dodatne simetrije, ki naj bi vladala Naravi, tako da bi imel vsak fermionski delec (to so delci s spinom 1/2, v Standardnem modelu so to kvarki in leptoni) svojega partnerja, skvarke in sleptone, ki pa bi imeli spin 0 (take delce imenujemo skalarji). Supersimetrija seveda ni natančna simetrija Narave, saj v eksperimentih ne opazimo skvarkov in sleptonov. Če bi bila supersimetrija točna, bi namreč skvarki in sleptoni morali imeti enake mase kot jih imajo kvarki in leptoni. Ker jih ne opazimo, lahko od tu sklepamo, da je supersimetrija zlomljena, skvarki in sleptoni imajo večje mase kot delci Standardnega modela. Vendar pa obstajajo teoretični argumenti, zakaj naj mase skvarkov in sleptonov ne bi bile prevelike. Če je supersimetrija resnično v povezavi z našim svetom, tedaj lahko pričakujemo, da jo bomo odkrili na trkalniku LHC. Prihodnost fizike delcev je svetla!
In sedaj še kratek odgovor na tvoje vprašanje, ali lahko iz težkih kvarkov in težkih leptonov sestavimo povsem nove elemente. V laboratorijih so sestavili že kar veliko hadronov (to so delci, ki čutijo močno interakcijo, na primer nevtron, proton in njuni sorodniki), ki vsebujejo težke delce, mezoni B tako vsebujejo kvark b (in lahki antikvark, u, d ali s), mezoni D kvark c, medtem, ko hadronov, ki bi vsebovali kvark t ni, saj kvark t razpade predno se lahko veže z lahkim antikvarkom v vezano stanje. Vsi tovrstni hadroni relativno hitro razpadajo (ker razpadata težka kvarka b in c), v približno 10 -12 s. Da bi tvorili “elemente”, bi morali vezati skupaj več hadronov, ker pa ti hitro razpadajo je to precej težavno. Numerične simulacije sicer kažejo na morebitni obstoj težkih dimezonov (dveh težkih mezonov vezanih skupaj), vendar pa eksperimentalne potrditve o tem ni. So pa že uspeli narediti atome, kjer so en elektron zamenjali z mionom. Tovrstni mionski atomi razpadejo v nekaj mikrosekundah (ker razpade mion). Ker pa je mion precej težji od elektrona, ima na primer mionski vodik precej manjši premer kot navadni vodik. Kar nekaj časa je zato obstajalo upanje, da bi mionske atome lahko uporabljali kot katalizator za fuzijo, a so bili tovrstni poskusi za sedaj neuspešni.