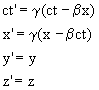Diskretni čas

Ideja diskretnega časa se vsekakor zdi vabljiva, posebno potem, ko se srečamo s kvantno mehaniko in njenimi diskretnimi energijskimi stanji. Tu človeka zlahka začnejo srbeti prsti, da bi se poigral še z diskretizacijo kakšne druge količine. Vendar pa, ali lahko nekaj takega naredimo tudi s časom?

V običajni fiziki majhnih hitrosti (v primerjavi s svetlobno) čas obravnavamo kot zunanji parameter, ki je absoluten ne glede na to, kje se nahajamo, tako da načeloma z diskretizacijo časa v tem opisu ne naletimo na večje probleme. Svet bi se pač namesto zvezno spreminjal sunkovito, tako kot gibanje roke osvetljene s stroboskopsko lučjo. Problemi pa nastanejo takoj, ko se preselimo v svet relativnosti. Sedaj se nam časovna dimenzija in prostor pomešata v celoto. Razumljivo se torej zdi, da z idejo o diskretnem času kaj hitro zaidemo v težave.

Poglejmo si težave še nekoliko podrobneje. Za razpravo potrebujemo pojem transformacij. Le te nam koordinate iz mirujočega sistema S preslikajo v koordinate v gibajočem sistemu S. Tako imenovana Lorentzova transformacija, zapisana za primer gibanja sistema S v smeri osi x s hitrostjo v, je

kjer je in . Da smo lahko izpeljali gornjo Lorentzovo transformacijo,

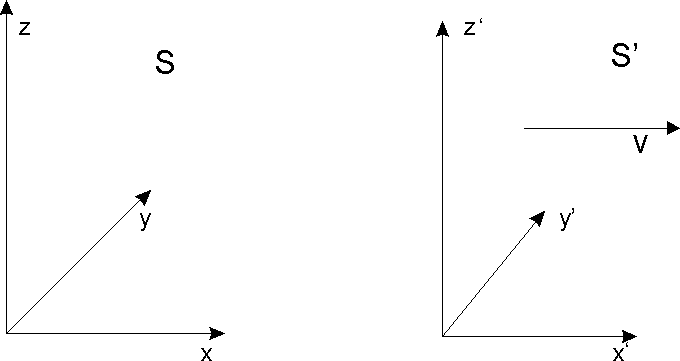
Slika1. Slika dveh sistemov, gibajočega S in mirujočega S.

smo morali privzeti, da je hitrost svetlobe c v vsakem inercialnem sistemu enaka, in da so si vsi inercialni sistemi enakovredni (fizika je v vseh enaka, ali drugače povedano, ne obstaja priviligiran koordinatni sistem glede na katerega bi merili hitrost). Prav tako opazimo, da pri gornji transformaciji koordinati pravokotni na smer gibanja (y in z) ostaneta nespremenjeni, zato ju v prihodnje izpustimo, tudi na slikah.

Kaj se spremeni, če čas diskretiziramo? Sprva predpostavimo, da se lahko lega teles spremeni le ob določenih časih, ki jih označimo s , in sicer po celotnem prostoru hkrati. Lorentzova transformacija v drug sistem S nam da

Gornji enačbi nam podajata parametrični zapis družine premic

torej premic oblike

Če sedaj vključimo v igro še preostali dve koordinati y in z, imamo sedaj opravka s hiper-ravninami v štiridimenzionalnem prostoru-času. In te ravnine se v splošnem ne ujemajo z ravninami konstantnega časa, kot je bilo to res v našem prvotnem sistemu S!

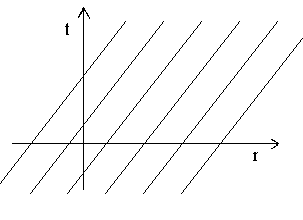
Slika2. Sistem S s poševnimi ravninami preskoka, na katerih lahko spremeni telo lego.

Preskoki lege se tedaj dogodijo v različnih delih prostora ob različnih časih. To si najlažje ponazorimo, če si tek časa predstavljamo kot ploskev konstantnega časa, ki se pomika vzdolž časovne koordinate. Le tedaj, ko se ploskev konstantnega časa in poševna ploskev preskoka ujemata, lahko telo preskoči na drugo pozicijo (tu izraz preskok morda ni več povsem ustrezen, saj lahko telo vedno ostane na isti poševni ravnini in se v bistvu giblje vzdolž x osi s primerno hitrostjo).

Na prvi pogled vse lepo in prav. A vendar smo s predpostavko o diskretnem času že zabredli v resne težave. Na tihem smo namreč privzeli, da tudi v diskretnem primeru veljajo Lorentzove transformacije. Za izpeljavo le teh pa smo, kot že rečeno, morali privzeti enakovrednost vseh inercialnih sistemov. Na žalost pa s prehodom na diskreten čas sistemi postanejo neenakovredni. Če nam namreč uspe določiti nagib hiper-ravnin v prostoru-času našega inercialnega sistema, lahko iz tega določimo hitrost našega sistema glede na referenčni sistem S, v katerem so preskoki po celem prostoru v istem trenutku. Obstaja torej možnost, da le z opazovanjem prostora-časa določimo svojo hitrost glede na referenčni sistem S. Vsakemu sistemu lahko tako predpišemo absolutno hitrost, ki ga seveda loči od ostalih. Ključno pri tem je, da lahko to hitrost določimo, ne da bi opazovali gibanje kakega drugega sistema (teles, ki mirujejo v njem), pač pa le z opazovanjem prostora-časa.

S tem, ko sistemi niso več enakovredni, pa izgubi verodostojnost tudi naše izvajanje samih Lorentzovih transformacij, tako da se celotna teorija zruši! Poizkušamo lahko tudi z izpeljavo takšnih transformacij, kjer bi bili preskoki leg v vsakem sistemu v istem trenutku (vsi sistemi bi imeli enako lastnost kot sistem S zgoraj), vendar pa so take transformacije v nasprotju z že izvedenimi eksperimenti.

(Jure Zupan)

-