Srednjeveška podoba univerzuma in njene antične predpostavke

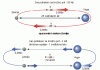
Kakšna je bila v visokem srednjem veku običajna, tipična podoba univerzuma, kot jo lahko rekonstruiramo iz literature o filozofiji narave? Vesolje, kot ga razumejo srednjeveški filozofi narave, je ogromna, enkratna, končna, materialna sfera, ki je vsepovsod napolnjena z materijo. Ta sfera je razdeljena v številne podsfere oziroma orbite, ki so posajene druga v drugo. Ta ogromna sfera je razdeljena na dva dela: nebesni in zemeljski oziroma supralunarni in sublunarni.^[1]

Dvodelni srednjeveški univerzum

Nebesni del se začenja s konkavnim površjem lunarne sfere in se dviga vse do sfere zvezd stalnic in celo onstran empirijskih nebes, najbolj zunanje sfere sveta, kjer naj bi živeli blaženi. Supralunarna regija je napolnjena s popolno, neminljivo substanco, petim bistvom, etrom, katerega osnovna lastnost je med drugim tudi zmožnost gibanja z enakomernim krožnim gibanjem ali pa zmožnost biti giban od česa drugega, na primer od angela oziroma inteligence. Ker so koncentrično urejene nebesne orbite, katerih število variira od osem do enajst, sestavljene iz etra, se gibljejo okoli središča našega sferičnega vesolja z enakomernim krožnim gibanjem in nosijo zvezde stalnice in sedem planetov. Osem sfer nosi nebesna telesa: osma sfera nosi sfero zvezd stalnic, sedem nižjih sfer pa sedem planetov.

Zemeljska regija se začenja pod konkavnim obličjem lunarne sfere in se spušča do geometričnega središča vesolja. V nasprotju z nebesno regijo je sublunarni svet zaznamovan z nenehnim spreminjanjem, v njej nepopolna telesa nenehno nastajajo in minevajo. Ta zemeljska telesa so sestavljena iz štirih elementov, ki so urejeni v nizu štirih koncentričnih orbit, vsaka od teh služi kot naravno mesto enega elementa. V sestopajočem redu od konkavne lunarne sfere navzdol je prva orbita naravno mesto ognja, druga zraka, tretja vode in četrta zemlje, ta predstavlja naravno in negibno središče univerzuma. Vsak element ima prirojeno zmožnost za naravno gibanje k svojemu naravnemu mestu. Prevladujoči element v vsakem telesu določa smer naravnega gibanja telesa, ki je vedno v smeri naravnega mesta prevladujočega elementa. Kadar zemeljska telesa niso ovirana, po naravi težka telesa vedno padajo proti središču vesolja, medtem ko se ognjena telesa, ki so absolutno lahka, dvigujejo proti lunarni konkavnosti. Ker je nebesna regija neminljiva in neuničljiva, je tudi popolnejša in zato odličnejša od zemeljske regije, v kateri negibna Zemlja skupaj s svojim središčnim položajem zavzema tudi najnepopolnejše in s tem najnižje mesto.

Antična kozmologija

Srednjeveška podoba univerzuma je kombinacija Aristotelovih in Ptolemajevih kozmoloških in astronomskih nazorov in dognanj, ter jo podpirata tako antična epistemologija kot antična fizika. Ptolemajev geocentrični sistem, ki ga je razvil v svojem slovitem delu Megale Syntaxis, znanem po arabskem naslovu Almagest, je namreč sinteza antičnih filozofskih nazorov o astronomiji, ki ji je program določil Platon, v detajle pa jo je razvil Aristotel.

Platonov astronomski program (reševanje pojavov)

Temeljni problem, ki je zaznamoval antično astronomijo, je dejstvo, da se na nebu poleg pravilnih gibanj zvezd stalnic, Sonca, Lune in planetov pojavljajo tudi nepravilnosti, ki jih ni mogoče pojasniti z geometrično pravilnimi gibanji. Na podlagi tega dejstva je Platon v Državi določil astronomiji nalogo, poiskati izza navidezne nepravilnosti idealni red: “Čudovite podobe zvezd na nebu vidnega sveta nam morajo sicer veljati za najlepše in najjasnejše podobe te vrste, vendar si moramo priznati, da daleč zaostajajo za resničnimi zvezdami in njihovim gibanjem, ki ga označujeta resnična hitrost in resnična počasnost v svetu resničnih števil in resničnih podob; ti dve hkrati spravljata v gibanje ves (resnični) svet, ki ga je moč dojeti samo z razumom in mislimi, ne pa z očesom.”^[2]

Platonov astronomski program napotuje astronomijo k temu, da izza navideznih nepravilnosti nebesnih gibanj odkriva popolno natančnost njihove idealne resničnosti. Cilj antičnega astronoma je torej naslednji: zvesti navidezne nepravilnosti gibanja zvezd na resnične zakone njihove idealne resničnosti ali, če rečemo z ustaljeno frazo, “reševati fenomene” (sotzein ta phainomena), se pravi “pojasniti fenomene, ohraniti jih oziroma odkriti tisto stvarnost, skrito pod njimi, pod navideznim neredom neposrednega dejstva odkriti neko dejansko, urejeno in intelegibilno enotnost”.^[3] Ta “metodološki princip stare astronomije o ‘reševanju pojavov'”^[4] je postavil in realiziral Platonov učenec Evdoks s Knida, dopolnil pa ga je Kalip iz Kizika: nepravilno in neenakomerno gibanje “planetov” sta pojasnila z enakomernim, krožnim, urejenim gibanjem, to je s teorijo homocentričnih oziroma koncentričnih (istosrediščnih) sfer, katerih središče je Zemlja.

Poenostavljena shema Evdoksovega modela kozmosa koncentričnih sfer.

Aristotelov hierarhični kozmos koncentričnih sfer

Aristotel je v temeljnih značilnostih povzel njuno teorijo, čeprav se od Evdoksa, ki mu je teorija homocentričnih sfer le matematična predpostavka, razlikuje v tem, da jemlje teorijo krožnega gibanja prvega neba in sfer, ki nosijo planete, za dejanskost, bitnost: “To ni zgolj teoretično, temveč dejansko (ergoi).”^[5] Aristotel sicer prevzame njuno geometrično konstrukcijo, “vendar pa uvede še drugačne, ‘nazaj vrteče se’ ali ‘reaktivne’ sfere, tako da se je celotno število sfer povečalo na 47 ali 55. Za to tezo je Aristotel menil, da ‘ustreza pojavom'”.^[6] Toda Aristotel se od Evdoksa in Kalipa razlikuje vsaj v dveh točkah.

Najprej po tem, da postanejo pri Aristotelu geometrijske krogle oziroma sfere materialna telesa iz “etra”, kajti večno krožno gibanje zahteva posebno bitnost: “Nujno je, da obstaja neka enostavna materija, ki se glede na svojo lastno naravo lahko premika v krožnem gibanju.”^[7] “To materijo, to primarno, prvotno telo (to proton soma), poleg zemlje in zraka, ognja in vode, je tradicionalna “modrost” imenovala aither, to pa je poimenovanje, postavljeno zato, ker aither “vedno teče v večnem času (apu tou thein aei ton aidion chronon).”^[8]

Od Evdoksa in Kalipa se Aristotel razlikuje tudi po tem, da v nasprotju od njiju, ki sta, da bi razložila gibanje planetov, kot ga je mogoče opazovati, sfere priredila vsakemu planetu posebej, vse koncentrične sfere vključuje v enoten geocentričen sistem.

Predpostavka teorije, ki rešuje fenomene s homocentričnimi krogi, je torej teza o načelni neprimerljivosti zemeljskih in nebesnih fenomenov.^[9] Medtem ko v sublunarnem svetu ogenj, zemlja, zrak in voda sledijo svojim zakonom, je v supralunarni sferi quinta essentia podvržena radikalno drugačnim pravilom. Medtem ko so ogenj, zemlja, zrak in voda v nenehnem procesu spreminjanja, je “peti element” eter načelno nespremenljiv, edina vrsta spremenljivosti, ki mu jo lahko pripišemo, je sprememba mesta, se pravi zgolj premikanje z enega mesta na drugo, prostorsko gibanje. Toda tudi v tem pogledu se svet zvezd razlikuje od sublunarne regije: v sublunarnem svetu ima sleherno gibanje, če izgubi podporo “od zunaj”, začetek in konec v času in prostoru, a nebesno gibanje zvezd je nujno misliti kot večno, kajti samo tako za supralunarno sfero ne veljajo zakoni spreminjanja. Čiste oblike gibanja, ki trajajo večno, so za antične astronome in tudi za Platona in Aristotela zgolj krožna gibanja.^[10] Samo krožno gibanje ima konstantno hitrost in je sklenjeno in kontinuirano. Ob predpostavki končnega sveta — in svet je, kot bomo videli, zaradi različnih razlogov za Aristotela lahko samo končen — je edino gibanje, ki ga je mogoče pripisati “prvemu nebu”, to je sferi zvezd stalnic, krožno gibanje. Premočrtno gibanje namreč ob tej predpostavki ne more biti hkrati neskončno in sklenjeno oziroma premočrtno enakomerno. Na podlagi te ugotovitve dokazuje Aristotel primarnost krožnega gibanja ali kroženja. Kroženje je primarno: (1.) ker je enostavno in popolno; (2.) ker je večno, saj je pri krožnem gibanju sleherna meja na enak način začetek, sredina in konec; (3.) ker je krožno gibanje (periphora, revolutio) neka časovna mera vseh drugih gibanj in mora zato biti nekaj primarnega, saj se vse meri s primarnostjo; (4.) ker je samo krožno gibanje enakomerno oziroma uniformno.

Iz teh predpostavk sledita dva temeljna aksioma antične astronomije: (1.) idealne tirnice gibanja zvezd so ali krožnice ali sestavljene iz njih; (2.) tiri, ki jih opisujejo zvezde, imajo enakomerno hitrost.

Aleksandrijska šola – vpeljava epicikov in ekvantov

Ti dve predpostavki je Kalipova teorija homocentričnih sfer ohranjala, poskusili pa so jih ohraniti tudi potem, ko se je pojavil problem različnega sijaja planetov, in je bilo mogoče to pojasniti samo s sprejetjem njihove oddaljenosti od Zemlje. Ta težava je spodbudila razvoj teorije epiciklov in ekscentričnih krogov, kar je razdelala aleksandrijska šola — Apolonij, Hiparh in Ptolemaj — in ki je prevladovala vse do Kopernika in v nekaterih glavah še kasneje. Ker razdalja planetov do Zemlje ni vedno ista, ker se planeti približujejo in oddaljujejo od Zemlje in ker se obenem tudi ne gibljejo enakomerno — zdi se, da gredo naprej, da se ustavijo in se gibljejo nazaj (retrogradno), zankasto, — je potrebno pojasniti dejstvo, da se idealne krožnice zvezd zdijo zemeljskemu opazovalcu kot zanke (pentlje), in tudi, zakaj je na nebu poleg pravilnega enakomernega gibanja tudi neuniformno gibanje.

Težavo z nepravilnostjo gibanja planetov ta teorija rešuje tako, da se planeti ne gibljejo po enem krogu, temveč po dveh ali treh, tako da je za prvi krog obešen drugi, manjši, ali pa je večji krog postavljen na manjšega. Krog nosilec je imenovan deferent, tisti, ki je na njem, pa epicikel. Tako je tisto, kar se nam zdi neuniformno, v resnici sestavljeno iz več uniformnih krožnic.

Edini problem, ki ga je imela ta teorija, je, da mora Ptolemaj zato, da ne bi povečeval števila krogov, ki jih potrebuje za pojasnitev, odstopiti od načela enakomernega krožnega gibanja oziroma najti način, da od njega ne odstopi, tako da na videz uskladi sprejemanje tega načela z nemožnostjo, da ga v resnici upošteva. Ptolemaj je izhod iz te zagate našel v tem, da je sprejel, da je gibanje enakomerno, toda ne v razmerju do svojega središča, temveč v razmerju do neke ekscentrične točke v krogu, ki jo je imenoval ekvant. Zemlja tako ne leži niti v geometričnem središču koncentričnih krožnic niti ne predstavlja resničnega središča gibanja, ampak je glede na geometrično središče vesolja ekscentrična, tako kot tudi resnično središče gibanja — to je punctus equans. Zahtevana enakomernost gibanja planetov je zdaj privzeta glede na to imaginarno, nematerialno točko zunaj Zemlje.

Shema geocentričnega univerzuma. 

Aristotelovi argumenti proti neskončnosti univerzuma

Preden zaključimo to kratko predstavitev osnovnih kozmoloških, fizikalnih in epistemoloških predpostavk tradicionalne podobe univerzuma, pojasnimo še razloge, ki so Aristotela prepričali o tem, da je svet nujno končen. Kako Aristotel utemeljuje sklep, da kozmos ne more biti neskončen?^[11]

Aristotel se vprašanja neskončnosti (apeiron) oziroma brezmejnosti ali neomejenosti loteva na podlagi predhodnih filozofemov, ki so se na tak ali drugačen način dotikali problematike neskončnega.^[12] S svojimi predhodniki se strinja, da je apeiron počelo oziroma princip, ki ni nastal in je neminljiv, katerega konceptualizacija pa je težavna, saj tako v primeru, ko trdimo, da neskončno obstaja, kot v primeru, ko obstoj neskončnega zanikamo, nastopijo absurdne posledice. Predvsem pa Aristotela vprašanje neskončnosti zanima z empiricističnega vidika, se pravi, ali je karkoli lahko neskončno v naravi (karkoli v časovnem in prostorskem svetu), predvsem pa, ali obstaja neskončna čutnozaznavna velikost oziroma telo. V tem kontekstu definira apeiron kot tisto, česar ni mogoče “preiti” (dielthein), kar je “neprehodno”, in ga razdeli na neskončno z dodajanjem (neskončno veliko) in neskončno z delitvijo (neskončno majhno). Zavrača tako Anaksimandrovo stališče, da je neskončno neka substanca sama po sebi, in tudi atomistično stališče, da je neskončnost lastnost mnoštva, saj ne verjame v idejo neskončnega števila: število je zanj namreč nekaj, do česar pridemo s štetjem, štetje v neskončnost pa bi pomenilo prehod skozi neskončen niz števil. Aristotela torej ne zanima, ali obstaja neskončno mnoštvo posameznih stvari, edino vprašanje, ki si ga v zvezi z neskončnostjo resnično postavlja, je, ali je kakšna posamezna stvar, npr. voda ali zrak itd., neskončna? To je v bistvu tudi vprašanje o možnosti obstoja neskončnega telesa.

Čeprav je telo že per definitionem nekaj končnega, saj je definicija telesa, da je omejeno s površino, pa razvije Aristotel za nemožnost nekončnega telesa celo serijo dokazov, ki temeljijo na njegovi fiziki, natančneje, na njegovem konceptu narave in naravnega gibanja. Zakaj torej nobeno telo (to pomeni kozmos) po Aristotelu ne more biti neskončno veliko?

Zakaj nobeno telo ne more biti neskončno?

Prvi fizikalni argument pravi, da neskončno telo ne more biti niti sestavljeno niti enostavno. V primeru (iz več teles) sestavljenega neskončnega materialnega telesa, ob predpostavki, da je teles končno mnogo (toda več kot eno), ni mogoče, da bi bilo samo eno od osnovnih teles (ogenj, zrak, voda, zemlja) neskončno, kajti neskočno telo bi v tem primeru uničilo končno telo,  niti ne morejo biti neskončna vsa telesa hkrati, ker bi se tako vsako raztezalo v neskončnost v vseh smereh, tako pa bi vsako posamezno neskončno telo dopuščalo samo končen prostor za ostale elemente. Ravno tako ne more obstajati eno enostavno neskončno telo, kajti takega enostavno ni v tvarnem svetu, pa tudi če bi predpostavili, da je kakšno, bi to izničilo ostale, tako kot voda izniči ogenj.

Naslednji argument izhaja iz Aristotelovega načela, da ima vsako fizično telo svoje naravno mesto, v smeri katerega se po svoji naravi giblje in v katerem je po svoji naravi na miru. In še več, vsak del celotnega telesa mora po naravi mirovati kjerkoli znotraj naravnega mesta celote, naravno mesto celote pa mora biti dovolj veliko, da sprejme celotno telo. Če bi obstajalo neskončno homogeno telo, bi bilo njegovo naravno mesto neskončno razsežno. Poglejmo katerikoli del tega telesa. Ta mora ali naravno vsepovsod mirovati, v tem primeru ne bo naravnega gibanja (in tudi ne nenaravnega, prisiljenega gibanja, ki je odvisno od naravnega gibanja), ali pa naravno gibanje ne bo nikjer v stanju mirovanja, v tem primeru naravno gibanje ne bo imelo konca. Toda tudi to je nemogoče, kajti v neskončni razsežnosti ne more biti privilegiranih mest oziroma smeri, ki bi določale gibanje. Če neskončno telo ne bi bilo homogeno, bi imel vsak del svoje naravno mesto, telo pa bi bilo poenoteno “s stikom”. Kakorkoli, da končno število delov neskončnega telesa ne more obstajati, je Aristotel že pokazal, ne more pa obstajati niti neskončno mnogo različnih delov, kot je pokazal v De caelo III, 4.^[13]

Nadaljnji argumenti proti obstoju neskončnega telesa so še naslednji: (1.) Predpostavka neskončnega čutnozaznavnega telesa je v nasprotju z Aristotelovo tezo, da se vsako tako telo giblje po svoji naravi ali “gor”, stran od središča, ali “dol”, proti središču.^[14] (2.) V neskončni razsežnosti ni nobenega temelja, na podlagi katerega bi lahko napravili absolutno distinkcijo med “zgoraj” in “spodaj”, med “levo” in “desno” ter med “naprej” in “nazaj”, kar so distinkcije, ki so po Aristotelu nujne za gibanje. (3.) Vsako telo je “na mestu”, zaseda določen mesto v prostoru, toda neskončno telo bi moralo biti v neskončnem mestu, ki pa ne more obstajati, torej ne more obstajati niti neskončno telo.

Argumenti v prid obstoja neskončnosti

To so argumenti, ki govorijo proti obstoju neskončnega. Toda na drugi strani obstaja cel niz razlogov, ki govorijo v prid obstoja neskončnosti, ki pa je drugačne vrste od neskončnosti telesa. Prvi razlog, ki govori za obstoj neskončnega, zadeva čas, saj se zdi, da je čas neskončen. Aristotel^[15] ne priznava, da bi čas imel začetek in konec. Drugi razlog zadeva delitev velikosti, saj matematiki uporabljajo neskončno delitev. V evklidski geometriji je vsaka črta deljiva ad infinitum, na podlagi tega pa je mogoče sklepati, da to v načelu velja tudi za fizični svet. Sklepati je mogoče, da vsaka črta (ali pa tudi čvrsto telo), tako abstraktno kot konkretno, vsebuje neskončno število delov. Aristotel zavrača tudi nedeljive velikosti. Tretji razlog, ki podpira tezo o obstoju neskončnega, se nanaša na kontinuirano porajanje in minevanje novih stvari, kar je integralni del naravnega dogajanja in ne bi bilo mogoče brez neskončnega dotoka materije. Četrtič, zdi se, da je vse, kar je omejeno ali končno, omejeno z nečim, kar je izven tega, tako da ne more obstajati zadnja meja ničesar. In nazadnje in najpomembnejše: zdi se, da je apriorna resnica matematike, ne samo da je niz naravnih števil neskončen, temveč tudi, da so neskončne matematične velikosti in da je neskončno tisto, kar je izza nebes. Za vsakim številom si lahko predstavljamo še večje število, za vsakim geometrijskim likom še večji lik, za vsako končno velikostjo še večjo “onstran” te.

Dva pomena neskončnosti: potencialna in aktualna neskončnost

V primeru, da neskončnost ne obstaja, kar bi lahko bila implikacija nemožnosti obstoja neskončnega telesa, potem ima čas začetek in konec, deljive velikosti ne obstajajo, ni niti neskočnosti pri številih. Aristotel torej tretjega in četrtega razloga, ki ju je navajal v podporo tezi o obstoju neskončnosti, nima za relevantna, za ostale tri pa ponuja rešitev, in sicer tako, da ločuje dva pomena neskončnosti: neskončno na neki način “je”, na neki način pa “ni”. “Biti” oziroma “je” lahko pomeni “biti potencialno”, “biti v možnosti” ali pa “biti dejansko”. Neskončno ne more “biti” aktualno, dejansko, lahko pa “je” potencialno. Kaj to natančno pomeni? Kako je nekaj potencialno neskončno, razloži Aristotel z zgledom potencialne neskončne deljivosti črte, pri čemer opozarja, da je treba potencialnost v tem primeru razumeti drugače kot v primeru potencialnosti kipa v bronu, kjer potencialnost brona dejansko postaja aktualnost kipa. Neskončnost “je potencialna” v pomenu, da se ne more realizirati v celoti, vsa naenkrat, v nekem določenem času, kot je to mogoče pri potencialnosti brona. “Biti” se izreka na več načinov, in eden teh je tudi ta, da nekatere stvari “so” (dejansko), četudi vsi njihovi deli še niso aktualizirani: na ta način “je” dan ali pa “so” olimpijske igre. Ta pomen “biti” dopušča distinkcijo med “aktualno” in “potencialno”: čeprav ni nujno, da bodo naslednje olimpijske igre prirejene, je še vedno pravilno reči, da olimpijske igre so, če to razumemo kot potencialno eksistenco olimpijskih iger.

Aristotelova razrešitev problema neskončnosti: aktualne neskončnosti ni

Na splošno, pravi Aristotel, je neskončno na način, da se ena stvar nenehoma jemlje za drugo — vsaka vzeta stvar je končna, toda tej vedno sledi druga. Tako so neskončni čas, človeška vrsta ter niz števil in tako je deljiva črta. Neskočnost je za Aristotela torej popolnoma sprejemljiva, pod pogojem, da ne obstaja “vsa naenkrat”, aktualno oziroma dejansko, ampak kot možnost, da obstaja potencialno. Ali rečeno nekoliko drugače: nekaj je lahko potencialno neskončno, ne more pa biti dejansko neskončno. S tako rešitvijo Aristotel lahko zavrne neskončnost, kar pomeni, da zavrača aktualno, dejansko neskončnost, in obenem sprejme neskončnost, ampak samo kot potencialno neskončnost. Neskončno torej ni tisto, kar imajo običajno za neskončno: “Neskončno ni to, zunaj česar ni ničesar, marveč to, zunaj česar je vselej nekaj.”^[16] Aristotel torej eksplicitno poudarja, da je neskončno nekaj, kar je necelo, kar ima vedno neki del zunaj sebe, to je v očitnem nasprotju s tradicionalnim razumevanjem neskončnega kot celega in dovršenega. “Neskončno je torej tisto, čemur je mogoče, ko se mu glede na kvantiteto karkoli vzame, vzeti še kaj, kar je zunaj.”^[17] To je ravno nasprotno od definicije celega in dovršenega. Neskončno ni tisto, kar nima ničesar zunaj sebe, (nič ni dejansko neskončno), temveč je neskončno tisto, kar ima vedno nekaj zunaj (to je denimo potencialna neskončnost števil). S tem Aristotel vzpostavi neko distinkcijo med dvema razumevanjema neskončnosti, kar bi lahko poimenovali z razliko med “matematičnim” neskončnim in “metafizičnim” neskončnim (celo, dovršeno, enotno) — distinkcijo, ki je odigrala odločilno vlogo tudi v krščanstvu.

Zakaj univerzum ne more biti potencialno neskončen?

Na podlagi svoje rešitve lahko Aristotel sprejme neskončnost “z dodajanjem” naravnih števil, ki so zanj abstrakcije stvari in procesov naravnega sveta, kar ne pomeni, da obstaja neskončno mnogo števil, niti ne, da je kako posamezno število neskončno, temveč da ni konca v procesu štetja. Neskončna kvantiteta je za Aristotela, kot smo videli, taka kvantiteta, pri kateri lahko vedno vzamemo še neki del, ki je za tistim oziroma čez tisto, kar je bilo že vzeto. Pri številih ne obstaja neskončnost “z delitvijo”, kajti enica je prvo nedeljivo počelo števil. Ravno tako je lahko sprejel neskočnost časa, ki je neskončen tako “z delitvijo” kot tudi “z dodajanjem”. Toda, kar zadeva neskončnost z dodajanjem v primeru določene kvantitete (oziroma kozmosa), Aristotel — na podlagi napačnega sklepanja — zatrjuje, da ne more biti ne dejansko ne potencialno neskončnega univerzuma, kar je seveda v protislovju s tem, kar je zatrdil glede potencialne neskončnosti časa ali človeške vrste. Če drži, da ne more obstajati dejansko neskončno razsežno telo, kot naj bi dokazal, to še ne pomeni, da ne more obstajati potencialno neskončno telo, ki bi vključevalo kontinuirano, neomejeno širitev nekega vedno končnega univerzuma. Aristotel tu uporabi dodatno premiso, da velikost univerzuma ni samo končna, temveč tudi določena, nekaj, kar verjetno jemlje kot samo po sebi umevno, saj pravi, da zato, ker ne obstaja neskončna čutnozaznavna velikost, tudi ne more biti preseganja vsake določene velikosti, kajti v tem primeru bi obstajalo nekaj, kar je večje kot svet. Da kozmos ne more biti niti potencialno neskončen, je konec koncev posledica Aristotelovega prepričanja, da je “materija <kozmosa> večna in da ni nič narejenega iz nič”,^[18] prepričanja, da svet vsebuje vso obstoječo materijo, vso materijo, ki lahko obstaja, in da ta materija obstaja v omejeni količini. Rečeno drugače, Aristotel ni nikoli pozabil, da nič ne nastane iz nič, ali še drugače, Aristotel ni dopuščal možnosti, da bi lahko neka moč kaj ustvarila iz nič.

Povzetek

Če povzamemo. Antični model kozmosa, ki ga povzame srednji vek, je Aristotelova konkretizacija platonskega mita in Evdoksove teorije: temelji na razumu in redu, v njem pa prevladuje estetska privlačnost kroga, sfere in orbitalnega gibanja. Po tem modelu je v središču vesolja mirujoča Zemlja, okoli katere krožijo Lunini planeti (Merkur in Venera), Sonce in trije zunanji planeti (Mars, Jupiter in Saturn), na skrajnem obodu vesolja je sfera zvezd stalnic in ta se giblje v nasprotni smeri. Lepota in organizacija tega sistem je razumljena kot dokaz božanske organizacije sistema in se upira vsakemu poskusu, ki bi želel mirujočo Zemljo premakniti iz njenega središča (pitagorejski ogenj, Aristarhov heliocentizem). Ko postane opazovanje planetov bolj natančno, se Aristotelov model izkaže za manj zadovoljivega, toda to pomanjkljivost so reševali z vpeljavo ekscentričnih krogov, kjer središče ne sovpade s središčem planetarne orbite, ali z epicikli, serijo minikrogov, ki so jim sledili planeti, ko so se gibali po večji krožnici okoli Zemlje. Ta koncept modela je “obdržal” Zemljo negibno, nepopolno, temno in težko v središču sklenjenega končnega kozmosa, hkrati pa je upošteval vse bolj in bolj kompleksne fenomene, tako da je kulminiral s Ptolemajevim sistemom, ki je uvedel še ekvant, hipotetično središče, v katerem sta združena idealno in realno središče.^[19]

(Članek je prirejeno poglavje IV/1 iz knjige: M. Vesel, Učena nevednost Nikolaja Kuzanskega, Zbirka Philosophica, Filozofski inštitiut ZRC SAZU 2000.)

-