Kvantna kromodinamika oziroma krajše kar QCD po kratici, ki izhaja iz angleškega poimenovanja Quantum Chromodynamics, je sodobna teorija močne jedrske sile, to je sile, ki veže nevtrone in protone v jedra. Pravzaprav bi imel fizik, ko bi omenjal kvatno kromodinamiko, navadno v mislih interakcije med kvarki, to je med subatomskimi delci, ki tvorijo nevtrone in protone, a več o tem v nadaljevanju. Sami začetki kvantne kromodinamike segajo v zgodnja sedemdeseta leta prejšnjega stoletja. V trideset in več letih svojega obstoja pa je bila sama teorija tako prepričljivo potrjena, da imajo mlajše generacije fizikov visoke energije njen obstoj za skorajda samoumeven. Če bi na primer pred dvajsetimi leti pri eksperimentih na visokoenergijskih trkalnikih morda še govorili o testih QCD, pa danes slišimo le še o računanju QCD popravkov k drugim zanimivim procesom.
Da vedno temu ni bilo tako govori tudi Nobelova nagrada za l. 2004, ki so jo prejeli teoretični fiziki David Gross, Frank Wilczek in David Politzer za “odkritje asimptotske svobode v teoriji močne interakcije“. To je bilo eno ključnih odkritij, ki je pripeljalo do sprejetja kvantne kromodinamike kot veljavne teorije močne interakcije. Ker sem navrgel kar nekaj pojmov brez pojasnila, si najprej oglejmo, kakšna sploh je struktura QCD kot teorije in kaj pomeni skrivnostni pojem asimptotske svobode v pojasnilu Nobelove nagrade, nakar se bomo vrnili k zabavnim zgodbam, ki so povezana s samim odkritje asimptotske svobode.

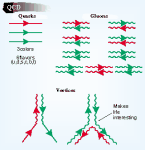
Da bomo lažje razumeli osnove kvantne kromodinamike, si najprej oglejmo njeno sestrično, kvatno elektrodinamiko, ali QED (Quantum Electrodynamics). QED je alma mater kvatnih teorij polja (skupine kvantnih teorij v katero spada tudi QCD), saj ima svoje korenine že v zgodnjih štiridesetih letih prejšnjega stoletja. V njej nastopajo elektroni, delci s spinom 1/2, kot predstavniki materije in fotoni, brezmasni delci s spinom 1, kot nosilci interakcije. Elektroni so električno nabiti, tako da interagirajo s fotoni. To lahko grafično predstavimo s tako imenovanimi Feynmanovimi diagrami. Najenostavnejši predstavnik takega Feynmanovega diagrama je na sliki zgoraj. Polni črti s puščicama predstavljata elektron, vijugasta črta pa foton, ki ga elektron izseva. Vendar pa Feynmanovi diagrami niso le nekakšno grafično mahanje z rokami, da bi približno pojasnili kaj se dogaja z elektronom. V resnici so to grafične predstavitve računa, ki napove verjetnost za proces, ki ga posamezen diagram predstavlja. Za vsakim narisanim diagramom torej stoji računski algoritem. V računu vsaka linija predstavlja kinematični faktor – propagator, vsako stičišče linij pa dodatni interakcijski faktor. Da bi dobili elektromagnetno silo med dvema elektronoma bi na primer morali izračunati Feynmanov diagram v katerem prvi elektron izseva foton, drugi pa ga absorbira.
V tem grafične jeziku izgleda QCD le kot razširitev QED. V QCD namesto elektronov nastopajo kvarki, delci s spinom 1/2, ki namesto električnega nosijo barvni naboj (tu sama barva nima prav nobene zveze z običajnim pojmom barve, ki smo ga navajeni iz običajnega življenja, kjer je barva le oznaka za del elektromagnetnega spektra). Da bomo povsem natančni: kvarki poleg barvnega nosijo dejansko tudi električni naboj, ki pa ni cel, temveč je +2e/3 za u,c,in t kvarke, ter –e/3 za d, s in b kvarke. Nosilci barvne interakcije so gluoni, brezmasni delci s spinom 1, ki imajo podobno vlogo kot fotoni v QED. Pomembna razlika med QCD in QED je, da obstajajo tri različne vrste barvnega naboja, medtem ko je v QED le ta le eden – električni. Povsem poljubno si lahko izberemo imena za te tri barvne naboje kot rdeč, zelen in moder naboj. Tako kot ustreza v QED pozitivnemu električnemu naboju negativni električni naboj, ustrezajo v QCD rdečemu, zelenemu in modremu naboju antirdeč, antizelen in antimoder naboj. Da nosi kvark antinaboj označimo tako, da obrnemo puščico na Feynmanovem diagramu.
Oglejmo si nekaj reprezentativnih Feynmanovih diagramov za kvantno kromodinamiko. Opazimo dve pomembni razliki v primerjavi s kvantno elektrodinamiko. Prva je posledica dejstva, da vsak gluon nosi en barvni in en antibarvni naboj. Interakcija z gluonom tako lahko spremeni npr. rdeče nabit kvark v zeleno nabit kvark, če interagira z gluonom, ki nosi antirdeč in zelen barvni naboj (z drugimi besedami, rdeč naboj kvarka in antirdeč naboj gluona se izničita, ostane le zelen naboj), kar je predstavljeno na zgornji sliki (glej diagram spodaj levo). Tovrstnega efekta v kvatni elektrodinamiki nimamo, saj interakcija elektrona s fotonom nikoli ne spremeni naboja elektronu. Sedaj še preštejmo število gluonov. Pričakovali bi, da imamo 3 (barve) x 3 (antibarve)=9 gluonov, vendar pa je v resnici eden od nabojev, ki je simetrično nabit, odveč. Tako imamo vsega skupaj osem različnih gluonov.
Druga razlika, ki je še pomembnejša, je, da lahko gluoni interagirajo tudi sami med seboj, saj nosijo barvni naboj. Tovrstnih interakcij zopet nimamo v kvantni elektrodinamiki, saj so fotoni nevtralni in ne morej neposredno interagirati med seboj. Tako na primer boji z laserskimi meči, ki smo jih lahko občudovali v Vojni zvezd, pravzaprav niso mogoči. Razen, če seveda niso meči dejansko delovali na gluonskem polju…
Asimptotska svoboda
Da so gluoni barvno nabiti in interagirajo med seboj ima pomembne posledice za obnašanje teorije. Oglejmo si moč interakcije, ko spreminjamo energijo pri kateri poteka reakcija (v žargonu bi rekli spreminjanje velikosti sklopitvene konstante, ko spreminjamo energijsko skalo). V QED bo sklopitvena konstanta naraščala, ko večamo energijo pri kateri recimo trčita elektron in pozitron. Dejansko to pomeni, da elektron občuti večji efektivni električni naboj pozitrona v trkih pri višjih energijah, kot pri nižjih energijah. Povsem nasprotno kot v QED pa v QCD velikost sklopitvene konstante močne sile pada z naraščajočo energijo (z drugimi besedami – efektivni močni naboj kvarkov z energijo pada)! Pri izredno velikih energijah trkov se bodo tako zdeli kvarki prosti, to je, kot da ne interagirajo z gluoni. To je pojem asimptotske svobode, za katerega odkritje so si Gross, Politzer in Wilczek zaslužili letošnjo Nobelovo nagrado za fiziko.
Celotna zgodba z odkritjem asimptotske svobode je pravzaprav kar zabavna. Prestavimo se v šestdeseta leta, ko so imele kvantne teorije polja kaj slab sloves med teoretičnimi fiziki. V računih so se namreč pojavljale neskončnosti za katere ni bilo povsem jasno, ali se jih je mogoče sistematično rešiti. Poleg tega je sama močna interakcija izgledala zaradi svoje izredno močne sile teoretično povsem neobvladljiva. Freeman Dyson je v 1950-tih celo pesimistično napovedal, da bo lahko minilo tudi 100 let, predno bomo dosegli pravilno teoretično razumevanje. Nato so prišli ključni eksperimenti v laboratoriju SLAC, Kalifornija. Skupina pod vodstvom Jeromea Friedmana, Henryja Kendalla in Richarda Taylorja je z globoko neelastičnim sipanjem elektronov na protonih pokazala, da so protoni sestavljeni iz delcev (za katere je Feynman uporabil ime partoni). Tedaj namreč še ni bilo jasno, da so partoni dejansko kvarki, o obstoju katerih sta že prej hipotetizirala Murray Gell-Mann in George Zweig (v tej zgodbi kar mrgoli Nobelovih nagrajencev, Friedman, Kendall in Taylor so za svoje eksperimentalno delo prejeli nagrado l. 1991, Gell-Mann pa za teoretično delo že leta 1969). Pri eksperimentih v SLACu so se kvarki/partoni obnašali, kot da so praktično prosti delci. To je bilo seveda povsem v nasprotju s siceršnjo velikostjo močne jedrske sile pri nizkih energijah, ki npr. trdno veže protone in nevtrone v jedra. Da mora pravilna teorija močne interakcije pojasniti tudi to asimptotsko svobodo, je bilo tako jasno že iz prelomnih eksperimentov v SLACu.
Konec l. 1972 se je David Gross skupaj s svojim podiplomskim študentom Frankom Wilczekom na univerzi Princeton namenil dokazati, da nobena kvatna teorija polja (kamor spada tudi kvantna kromodinamika) ne more biti asimptotsko svobodna. En takšen primer so že poznali, in sicer QED, ki res ni asimptotsko svobodna, saj moč interakcije z energijo narašča. Da bi pokazala to za vse kvantne teorije polja, sta morala izračunati tako imenovano beta funkcijo, ki kodira odvisnost sklopitvene konstante z energijo. Če je beta funkcija negativna, potem sklopitvena konstanta z energijo pada in teorija je asimptotsko svobodna, drugače pač ne. Ker je celotna interpretacija mukotrpnega računa beta funkcije odvisna od predznaka, si je seveda lahko predstavljati, da je iskanje napak v predznakih v računih ključnega pomena. Gross in Wilczek sta tako bila nekaj dni celo prepričana, da jima je uspel zadani cilj, namreč, da je beta funkcija QCD pozitivna.
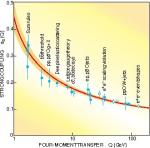
Neodvisno se je računa lotil tudi Politzer, podiplomski študent Sidneya Colemana na Harvardski univerzi. Coleman je bil spomladi l. 1973 ravno na sobotnem letu na Princetonu, ko mu je ves navdušen telefoniral Politzer, češ, da je izračunal, da je QCD asimptotsko svobodna teorija. Vendar pa je Coleman ohladil navdušenje svojega študenta, saj mu je Gross, pod vplivom napačnega predznaka v računu, ravno zatrdil, da QCD ne more biti asimptotsko svobodna. Wilczek je nato našel napako v računu, prav tako pa je bil Politzer po ponovnem preverjanju računa dovolj prepričan v negativni predznak beta funkcije. Članka o odkritju asimptotske svobode sta drug ob drugem izšla 25. junija 1973 v reviji Physical Review Letters. Eksperimentalno potrditev asimptotske svobode, to je zmanjševanje sklopitvene konstante z naraščajočo energijo, kaže spodnja slika.
Zanimivo pri tem je, da je nizozemski fizik ‘t Hooft že poleti 1972 vedel za negativni predznak beta funkcije QCD, na kar lahko sklepamo iz njegovega javnega komentarja na konverenci. Vendar pa njegov komentar ni bil širše znan, poleg tega je svoje rezultate objavil šele nekaj mesecev po obeh člankih. Kljub vsemu ‘t Hooft ni ostal praznih rok pri podeljevanju nagrad, saj je za svoje prejšnje delo na renormalizabilnosti Yang-Mills teorij (posebna kategorija kvantnih teorij polja, v katero spada tudi QCD) prejel skupaj s svojim menotrjem Martinusom Veltmanom Nobelovo nagrado l. 1999.
Pojem asimptotske svobode ima še svoj nasprotni pol. Ker velikost sklopitvene konstante z energijo pada, to po drugi strani tudi pomeni, da ob nizkih energijah sklopitvena konstanta narašča. Pravzaprav pri zelo nizkih energijah le ta naraste prek vseh mej. To z drugimi besedami pomeni, da moč močne jerske sile ob nizkih energijah, to je ob energijah, ki jih recimo srečamo pri interakcija kvarkov znotraj protonov, močno naraste. To vsaj kvalitativno pojasni, zakaj v naravi ne srečamo posameznih kvarkov, temveč so ti vedno po trije vezani (ujeti) v proton (dva u kvarka in en d kvark) ali pa nevtron (en u kvark in dva d kvarka). Tedaj namreč lahko kvarki tvorijo barvno nevtralno stanje, ki ni izvor dolgosežnega gluonskega polja. Močno interakcijo lahko drug proton začuti le, če se prvemu dovolj približa, da razloči posamezne barvne naboje kvarkov. Ta slika tako tudi pojasni majhni doseg močne jedrske interakcije.
Več o ozadju Nobelove nagrade za fiziko za leto 2004:
–Zapisi na Physics Today
–Uradna stran Nobelove nagrade
Jure Zupan