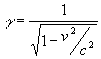Relativistična masa

V enačbo gravitacijskega privlaka vstopi relativistična masa (to pomeni mirovna masa, pomnožena s faktorjem

kjer v hitrost telesa in c svetlobna hitrost). Zakaj tako?

Ena od temeljnih predpostavk v splošni teoriji relativnosti (STR) pravi, da sta težka in vztrajnostna masa enaki (za definicijo glej odgovor na vprašanje o merjenju mase). To je Albert Einstein opisal (približno) takole:

“Postalo mi je jasno, da telo, ki prosto pada, ne čuti gravitacije“

Vztrajnostna in težka masa sta enaki, saj se njuna učinka pri prostem padu “kompenzirata”. Težka masa je “kriva” za gravitacijsko silo (z drugimi besedami: zaradi težke mase telo pada), vztrajnostna masa pa pove, kako se telo upira padanju. Zaradi ekvivalentnosti težke in vztrajnostne mase pa se oba učinka medsebojno kompenzirata.

Primer: Preden padalec odpre padalo prosto pada in v roki drži nek predmet (zamislimo si, da ni zračnega upora). Ko ga bo izpustil, bo predmet padal skupaj z njim. Padalcu se bo zdelo, da je v breztežnostnem prostoru (ko je predmet izpustil, mu ni padel na tla, ampak lebdi v zraku). Nekaj podobnega doživijo tudi astronavti na vesoljski postaji. Ko krožijo okoli Zemlje, so neprestano v prostem padu, zato ne občutijo teže.

Težka masa je odgovorna za gravitacijo, vztrajnostna masa pa pove, kako se telo upira spremembam gibanja. Poleg tega vztrajnostna masa nastopa tudi v izrazu za energijo

.

Ta izraz velja v klasični fiziki. V relativistični fiziki pa se močno poenostavljeno zapiše E = mc². Pri tem je m tako imenovana

relativistična masa: m = m₀g.

Lahko torej rečemo, da sta vztrajnostna masa in energija nekaj podobnega (razlikujeta se samo za faktor c²). Ker sta vztrajnostna in težka masa ekvivalentni, to pomeni, da tudi energija čuti gravitacijsko silo!

Da energija zares čuti gravitacijo, potrjuje eksperimentalna ugotovitev, da se pot svetlobe v bližini težkih teles (sonce) ukrivi. Poenostavljeno gledano lahko rečemo, da energiji, ki jo nosi svetloba, pripišemo težko maso m = E/c². Za pot masivnih teles pa je seveda jasno, da se v gravitacijskem polju ukloni.

Za zaključek pa še to: masa je izvor gravitacijske sile. Ker sta energija in masa ekvivalentni (razlikujeta se le za faktor), pričakujemo, da je tudi energija lahko izvir gravitacijske sile. V enačbah STR kot izvir polja nastopa tudi gostota energije.

Dodatno vprašanje: V enačbo gravitacijskega privlaka torej vstopa relativistična masa. V žepu imam 10 gramske ključe. Če mi jih uspe pospešiti do hitrosti, ki je dovolj blizu svetlobni, jih sicer ne bom mogel imeti v žepu, pač pa bodo imela vsa nebesna telesa v njihovem gravitacijskem polju neskončno potencialno energijo. Se motim? Ali bi moral potemtakem dovesti ključem med pospeševanjem tudi energijo, ki bi kompenzirala nenadejani energetski profit (v mislih imam potencialno energijo ostalih mas vesolja)?

Tvoje vprašanje je dosti bolj zvito kot si misliš. Za začetek tole: spremembe gravitacijske potencialne energije zaradi povečanja mase so zelo majhne. Npr. na Zemlji, je sprememba potencialne energije zaradi povečanja mase le pribl. 7*10^-10 krat sprememba kinetične energije. Torej: če si dal svojim ključem že toliko energije, da tehtajo 1 kg, se za spremembo 0.00000001 kg res ne boš sekiral.

Pa še to: če nekemu telesu v sistemu masivnih teles povečaš maso, se potencialna energija ZMANJŠA in ne poveča.

(Tadej Mali)

-