| Kakšna je kotna in energijska porazdelitev delcev pri razpadu jedra? Kako bi določili mesto, kjer se nahaja kvantni tunel (tj. mesto, kjer delec prečka bariero na grafu)? |
Jedra in njihova masa
Povejmo najprej nekaj splošnega o razpadu jeder in jedrih nasploh, da bo obravnava razpada ![]() jasnejša. Jedra sestojijo, kot vedo že vsi mali otroci, iz protonov in nevtronov. Koliko je protonov, nam pove vrstno število Z (velikokrat je to številka, ki v periodnem sistemu stoji levo spodaj pri znaku elementa). Število protonov določa element, medtem ko so izotopi atomi istega elementa, ki vsebujejo različno število nevtronov. Skupno število vseh nukleonov v jedru imenujemo masno število in ga tradicionalno označimo z A. Nevtronov je potemtakem A-Z. Pri razpadih jeder igra pomembno vlogo njihova masa, ki pa ni kar vsota mas nevtronov (m=939.6 MeV/c2 ali 1.67510-27 kg) in protonov (m=938.3 MeV/c2 ali 1.67310-27 kg). Upoštevati moramo namreč, da nukleoni niso prosti, temveč med njimi deluje takoimenovana močna jedrska sila, ki jih veže v jedro, upoštevati moramo tudi elektrostatski odboj in pa dejstvo da nosijo delci tudi kinetično energijo. Skupna vsota vseh treh prispevkov je negativna. Z uporabo Einsteinove slavne formule E=mc2, ki govori o dejstvu, da imata masa in energija podobno vlogo, lahko preberemo, da je zaradi interakcije med nukleoni skupna masa nastalega jedra manjša od vsote mas posameznih nevtronov in protonov. To razliko imenujemo vezavna energija in je, seveda izračunana na nukleon, večja pri močneje vezanih jedrih.
jasnejša. Jedra sestojijo, kot vedo že vsi mali otroci, iz protonov in nevtronov. Koliko je protonov, nam pove vrstno število Z (velikokrat je to številka, ki v periodnem sistemu stoji levo spodaj pri znaku elementa). Število protonov določa element, medtem ko so izotopi atomi istega elementa, ki vsebujejo različno število nevtronov. Skupno število vseh nukleonov v jedru imenujemo masno število in ga tradicionalno označimo z A. Nevtronov je potemtakem A-Z. Pri razpadih jeder igra pomembno vlogo njihova masa, ki pa ni kar vsota mas nevtronov (m=939.6 MeV/c2 ali 1.67510-27 kg) in protonov (m=938.3 MeV/c2 ali 1.67310-27 kg). Upoštevati moramo namreč, da nukleoni niso prosti, temveč med njimi deluje takoimenovana močna jedrska sila, ki jih veže v jedro, upoštevati moramo tudi elektrostatski odboj in pa dejstvo da nosijo delci tudi kinetično energijo. Skupna vsota vseh treh prispevkov je negativna. Z uporabo Einsteinove slavne formule E=mc2, ki govori o dejstvu, da imata masa in energija podobno vlogo, lahko preberemo, da je zaradi interakcije med nukleoni skupna masa nastalega jedra manjša od vsote mas posameznih nevtronov in protonov. To razliko imenujemo vezavna energija in je, seveda izračunana na nukleon, večja pri močneje vezanih jedrih.
Omenimo še pojem relativna atomska masa, ki zaznamuje povprečno maso elementa, to je povprečno maso vseh izotopov nekega elementa, pri čemer povprečje izračunamo glede na to, kako pogosti so posamezni izotopi v naravi. Zapišemo jo glede na maso ogljika 12C in je v splošnem neka necela številka, navadno zelo blizu masnemu številu najpogostejšega izotopa.
Razpad
Kdaj torej jedra razpadejo? Takrat, ko je skupna masa končnih produktov manjša od mase začetnega jedra, pri čemer se sprosti odvečna energija, ki je bila pred tem vezana v obliki mase začetnega jedra. Število nevtronov in protonov ostane pri razpadih preko močne jedrske interakcije nespremenjeno, spremeni se samo vezavna energija. Delci morajo na koncu biti močneje vezani (bolj negativna vsota kinetične in potencialne energije), kot so bili na začetku, da je razpad mogoč. Velika jedra lahko razpadejo na dve manjši, približno enako veliki jedri (cepitev jedra), ali pa izločijo delec ![]() (poznamo še ostale radioaktivne razpade na primer razpad
(poznamo še ostale radioaktivne razpade na primer razpad ![]() , ki pa poteka po šibki jedrski reakciji in ga tu ne obravnavamo). Delec
, ki pa poteka po šibki jedrski reakciji in ga tu ne obravnavamo). Delec ![]() ni nič drugega kot jedro helijevega atoma, dva protona in dva nevtrona. A vendar, zakaj nas tako zanima razpad jedra z oddajo štirih nukleonov, zakaj na primer jedro ne odda enega, dveh ali treh delcev raje kot štiri? Odgovor je preprost. Vezavna energija delca
ni nič drugega kot jedro helijevega atoma, dva protona in dva nevtrona. A vendar, zakaj nas tako zanima razpad jedra z oddajo štirih nukleonov, zakaj na primer jedro ne odda enega, dveh ali treh delcev raje kot štiri? Odgovor je preprost. Vezavna energija delca ![]() je precej večja od vezavnih energij manjših jeder (npr. vodika 1H, devterija 2H, tritija 3H ali 3He).. Razpad
je precej večja od vezavnih energij manjših jeder (npr. vodika 1H, devterija 2H, tritija 3H ali 3He).. Razpad ![]() je tako energijsko ugodnejši, kljub temu pa postane energijska razlika med končnim in začetnim stanjem negativna šele za jedra A > 140. Zakaj je verjetnost za razpad
je tako energijsko ugodnejši, kljub temu pa postane energijska razlika med končnim in začetnim stanjem negativna šele za jedra A > 140. Zakaj je verjetnost za razpad![]() znatna šele pri A > 200 bomo pojasnili v nadaljevanju.
znatna šele pri A > 200 bomo pojasnili v nadaljevanju.
Razpad ![]() in tunelski pojav
in tunelski pojav
Doslej smo se ukvarjali predvsem z močno jedrsko silo med nukleoni, ki je med protoni in nevtroni enaka, nič kaj zanemarljiva pa ni električna sila med protoni. Protoni so pozitivno nabiti in se odbijajo. Zato, da se stiskajo na tako majhnem prostoru kot je jedro (velikost jedra je 1-10 fm, 1fm=10-15 m) je kriva izključno močna sila, ki svoj vpliv popolnoma izgubi, ko se od jedra malo oddaljimo. Potencialna energija protonov je torej zelo negativna znotraj jedra, ko jih z močno jedrsko silo privlačijo nevtroni in ostali protoni, takoj malo vstran od jedrskega roba pa postane zaradi električnega odboja zelo pozitivna in pada z 1/r po Coulombovem zakonu (glej Sliko 1).
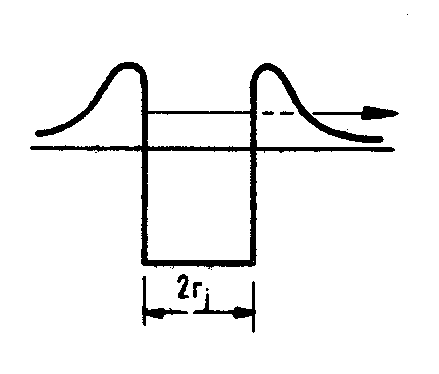
Slika 1: Približen potencial jedra za pozitivno nabit delec v odvisnosti od oddaljenosti r. Na sredini prevladuje privlačen jedrski potencial, zunaj pa odbojni električni.
V jedru imamo, kot že rečeno veliko število nukleonov, protonov in nevtronov, ki pa nimajo točno določene kinetične energije, pač pa se jim ta ob trkih z ostalimi nukleoni spreminja. Celotno dogajanje je, kot si lahko predstavljamo, precej dinamično. Zgodi se tako, da se na primer štirje nukeloni, dva protona in dva nevtrona znajdejo precej skupaj, za trenutek dobimo delec ![]() , ki se giblje v povprečnem potencialu kot ga ustvarjajo ostali nukleoni. Kinetična energija takšnega delca znotraj jedra je v primeru, ko je razpad mogoč, tolikšna, da tudi po prehodu bariere ta energija ostane pozitivna. Na sliki1 nam energijo delca
, ki se giblje v povprečnem potencialu kot ga ustvarjajo ostali nukleoni. Kinetična energija takšnega delca znotraj jedra je v primeru, ko je razpad mogoč, tolikšna, da tudi po prehodu bariere ta energija ostane pozitivna. Na sliki1 nam energijo delca ![]() prikazuje črta s puščico. Skupna energija delca je ne glede na to, kje se delec nahaja, nespremenjena. Znotraj jedra (znotraj elektrostatske bariere) ima večjo kinetično energijo- to predstavlja razlika med črto s puščico in dnom potenciala, zunaj jedra pa je kinetična energija manjša. Poleg teh dveh področij s pozitivno kinetično energijo opazimo tudi tretje področje, ko poteka črta pod potencialno bariero. Tu bi bila kinetična energija delca
prikazuje črta s puščico. Skupna energija delca je ne glede na to, kje se delec nahaja, nespremenjena. Znotraj jedra (znotraj elektrostatske bariere) ima večjo kinetično energijo- to predstavlja razlika med črto s puščico in dnom potenciala, zunaj jedra pa je kinetična energija manjša. Poleg teh dveh področij s pozitivno kinetično energijo opazimo tudi tretje področje, ko poteka črta pod potencialno bariero. Tu bi bila kinetična energija delca ![]() negativna!
negativna!
Po klasični mehaniki to ni možno, saj je energija v vsakem trenutku določena in se ne spreminja. Kvantna mehanika, ki je tukaj v veljavi, pa dovoljuje delcu, da ima za krajši časovni interval energijo večjo od svoje lastne povprečne energije, tako da lahko ubeži preko bariere. Energija namreč v kvantni mehaniki ni več določena v vsakem trenutku. V povprečju se sicer še vedno ohranja, za neki omejen časovni interval pa je lahko energija večja ali manjša od povprečne. To, da delec lahko predre območje, kjer je potencialna energija večja od delčeve skupne energije imenujemo tunelski pojav. Tukaj nimamo seveda nobenega tunela, po katerem bi delec potoval, temveč gre samo za analogijo z navadnimi tuneli. Namesto, da gremo čez, jo ucvremo skozi hrib.
Vendar pa verjetnost za takšno “tuneliranje” pada eksponentno tako z višino kot z debelino potencialne bariere. Delec, ki ima višjo energijo, bo tako lažje tuneliral, saj bo vrh bariere zanj nižji. Sedaj lahko tudi pojasnimo, zakaj je razpad pri jedrih z masnim številom okoli 140, kljub temu, da je mogoč, manj verjeten kot pri jedrih z A okoli 200. Pri prvih je namreč energija izhajajočega delca ![]() precej majhna (smo blizu praga za reakcijo), verjetnost za tuneliranje tako tudi razmeroma majhna.
precej majhna (smo blizu praga za reakcijo), verjetnost za tuneliranje tako tudi razmeroma majhna.
Zanimiva je tako tabela
| Jedro | E delca |
t1/2 |
| 144Nd | 1.8 MeV | 2 1015let |
| 238U | 4.18 MeV | 4.5 109let |
| 216Po | 6.77 MeV | 0.16 s |
| 212Po | 8.78 MeV | 3.10-7s |
Morda še kratek odgovor o vprašanju o točki tuneliranja. Kljub temu, da smo na sliki1 zarisali črto, ki nakazuje energijo delca ![]() , pa mesti, kjer ta seka potencialno bariero nista mesti tuneliranja. Delec alfa namreč ni lokaliziran v eni točki, njegovemu gibanju tako ne moremo predpisati trajektorije, ne vemo natančno kje se nahaja. Z določeno verjetnostno porazdelitvijo je le razmazan po celem jedru, kar je pač ena od manifestacij kvantnomehanske narave pojava.
, pa mesti, kjer ta seka potencialno bariero nista mesti tuneliranja. Delec alfa namreč ni lokaliziran v eni točki, njegovemu gibanju tako ne moremo predpisati trajektorije, ne vemo natančno kje se nahaja. Z določeno verjetnostno porazdelitvijo je le razmazan po celem jedru, kar je pač ena od manifestacij kvantnomehanske narave pojava.
In še kot zanimivost:
Glede na to, da imamo opraviti z dvodelčnim razpadom, kjer je kinetična energija končnega jedra in delca ![]() natanko določena prek izrekov o ohranitvi energije in gibalne količine, bi tako v energijskem spektru delcev
natanko določena prek izrekov o ohranitvi energije in gibalne količine, bi tako v energijskem spektru delcev ![]() pričakovali eno samo črto, dejansko pa jih dobimo več. Vzrok je v tem, da lahko jedro razpade tudi v vzbujena stanja novega jedra in ne samo v osnovno. Jedro ima namreč, kot vsak drug kvantnomehanski sistem, diskretne energijske nivoje. Razlika med osnovnim in vzbujenim jedrom je ta, da se, če si poskušamo stvar predstavljati klasično, nukleoni v vzbujenem stanju gibljejo intenzivneje kot v osnovnem. Ali drugače, njihova povprečna kinetična energija je višja. Ker ima pri razpadu v vzbujena stanja delec
pričakovali eno samo črto, dejansko pa jih dobimo več. Vzrok je v tem, da lahko jedro razpade tudi v vzbujena stanja novega jedra in ne samo v osnovno. Jedro ima namreč, kot vsak drug kvantnomehanski sistem, diskretne energijske nivoje. Razlika med osnovnim in vzbujenim jedrom je ta, da se, če si poskušamo stvar predstavljati klasično, nukleoni v vzbujenem stanju gibljejo intenzivneje kot v osnovnem. Ali drugače, njihova povprečna kinetična energija je višja. Ker ima pri razpadu v vzbujena stanja delec ![]() na razpolago manj energije, je verjetnost za razpad manjša in tako tudi intenziteta takšnih delcev upade (glej Sliko 2).
na razpolago manj energije, je verjetnost za razpad manjša in tako tudi intenziteta takšnih delcev upade (glej Sliko 2).
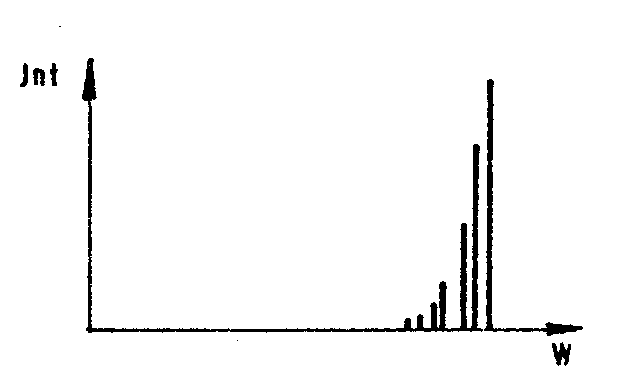
Slika 2: Graf intenzitete delcev ![]() v odvisnosti od njihove energije za razpad istega jedra. Delec
v odvisnosti od njihove energije za razpad istega jedra. Delec ![]() z največjo energijo ustreza razpadu v osnovno stanje, ostale črte potem ustrezajo prvemu, drugemu, n-temu vzbujenemu stanju. Odvisnost intenzitete za posamezne črte je eksponentna. Energija delcev
z največjo energijo ustreza razpadu v osnovno stanje, ostale črte potem ustrezajo prvemu, drugemu, n-temu vzbujenemu stanju. Odvisnost intenzitete za posamezne črte je eksponentna. Energija delcev ![]() se na splošno giblje med 1-10 Mev (1.6-16 10-13 J).
se na splošno giblje med 1-10 Mev (1.6-16 10-13 J).
Posebno poglavje je kotna porazdelitev izsevanih delcev alfa. Če ima jedro vrtilno količino nič, potem zanj ni nobene preferirane smeri in pričakujemo izotropno kotno porazdelitev. To pomeni, da delci alfa letijo v vse smeri z enako verjetnostjo. V primeru pa, ko vrtilna količina ni enaka nič, izotropnost ni več nujna. Kljub temu imamo v vzorcu, kjer opazujemo razpad alfa vedno ogromno jeder, ki so usmerjene v vse mogoče smeri in se njihova porazdelitev tako izpovpreči v izotropno. Kakšna bi bila kotna porazdelitev polariziranih jeder, to je takih, katerih vrtilna količina (spin jedra) bi bila usmerjena v isto smer, pa je nekoliko težje napovedati. Anizotropnost je namreč posledica anizotropnosti jedrskega potenciala jedra z neničelno vrtilno količino. Takšno jedro ni več okroglo, ampak bolj cigarasto ali v obliki diska. Ker je jedrski potencial odvisen od orientacije, tudi velikost elektrostatske bariere ni več v vseh smereh enaka. Delec alfa uide v različne smeri z različno verjetnostjo. Točno kotno porazdelitev bi bilo težko napovedati, saj je odvisna od natančne zgradbe jedra, poleg tega velja za vsako jedro drugačna porazdelitev. Računov pa se vseeno lahko lotimo v različnih približnih modelih.
Viri:
J. Strnad, Fizika 4.del, 1986 DMFA, visokošolski učbenik
M. Rosina, Jedrska Fizika, 1981 DMFA, visokošolski učbenik










