| Kakšna je definicija razpolovne dobe poljubnega radioaktivnega elementa? |
Najprej se pomudimo pri samem radioaktivnem razpadu. Poznamo radioaktivne razpade , 
in 
ter cepitev jedra, pri katerih stoji v ozadju različen mehanizem razpada atomskega jedra. Tako se pri razpadu izseva iz jedra delec , to je helijevo jedro, pri razpadu se izsevata elektron in nevtrino, pri razpadu preide vzbujeno jedro z izsevanjem visokoenergijskega fotona (žarki ) v nižje stanje, medtem ko se pri cepitvi jedro težkega elementa (npr. urana) razcepi na dve manjši jedri ter nekaj prostih nevtronov. Kljub vsej tej raznovrstnosti radioaktivnih razpadov, pa lahko opišemo verjetnost, da jedro po določenem stanju še ni razpadlo, z isto enačbo. Za vse te procese namreč verjetnost pada eksponetno.
Vzrok za to je dvojen. Prvi razlog za enostavno eksponentno odvisnost se skriva v tem, da je verjetnost za razpad neodvisna od okoliških jeder, t. j. ne zavisi od tega koliko jeder v okolici je že razpadlo. Verjetnost za razpad je odvisna le od posameznega jedra. Če temu ne bi bilo tako, bi bila časovna odvisnost mnogo bolj kompleksna. Drugi razlog za enostavno časovno odvisnost je prav tako vezan na statistično naravo pojava. Verjetnost, da jedro razpade v kratkem časovnem intervalu dt okoli nekega časa t, je namreč neodvisna od tega ali je to takoj po nastanku jedra (označimo to s t=0) ali pa pet minut zatem (t=5 min), če le jedro do časa t še ni razpadlo. Označimo s P(t) verjetnost, da jedro do časa t še ni razpadlo. Verjetnost da jedro tudi po preteku časa dt ni razpadlo se bo v intervalu dt zmanjšala za dP in sicer sorazmerno z dolžino časovnega intervala (sorazmernostno konstanto označimo z 
, kjer je 
razpadni čas) pomnoženo z verjetnostjo, da jedro do časa t še ni razpadlo ( kar smo označili s P(t)). Tako
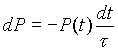
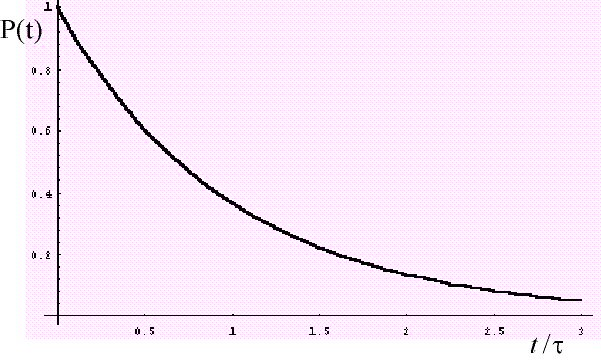
Rešitev gornje enačbe je eksponentni razpad
Če imamo tako na začetku 
radioaktivnih jeder, se bo število jeder N(t) v povprečju zmanjševalo eksponentno s časom
Eksponentno funkcijo lahko zapišemo tudi v drugačni obliki, kjer za osnovo ne vzamemo e, t.j. osnove naravnega logaritma. V navadi je definirati razpolovno dobo 
, to je čas v katerem se število nerazpadlih jeder prepolovi. Število nerazpadlih jeder se sedaj manjša po
Sedaj lahko preberemo tudi zvezo med razpadnim časom in razpolovno dobo
