| Kaj je to čudni atraktor? |
Trenutno stanje dinamičnega sistema opišemo z vrednostmi fizikalnih spremenljivk. V primeru gibanja delca so te spremenljivke delčeve koordinate in hitrosti, termodinamske sisteme opisujemo s temperaturo, tlakom, magnetizacijo (kadar imamo magnetno polje), električno polarizacijo (kadar imamo električno polje)… Prostor, v katerem vsaka točka natanko določa stanje sistema, imenujemo fazni prostor in vrednost vsake sistemske spremenljivke določa eno izmed koordinat točke v faznem prostoru (za gibanje delca v eni dimenziji je tako fazni prostor dvorazsežen, ena koordinata je hitrost delca, druga koordinata njegova lega). Spreminjanje sistemskih spremenljivk s časom in s tem gibanje točke v faznem prostoru določajo gibalne enačbe. Kadar ima sistem p sistemskih spremenljivk, je njegov fazni prostor p dimenzionalen in gibanje točke v tem faznem prostoru imenujemo tudi p dimenzionalni tok.
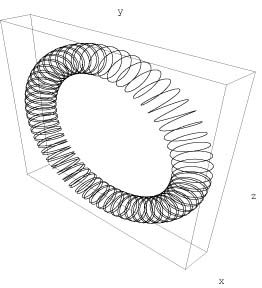
Disipacija v dinamičnih sistemih, kadar je le ta prisotna, povzroči, da se fazni prostor s časom krči v točke ali množice točk v faznem prostoru, ki jih imenujemo atraktorji. Po definiciji so atraktorji torej točke ali množice točk, h katerim se približujejo trajektorije v faznem prostoru, ko gre čas proti neskončno. Zajetje atraktorja imenujemo množico točk, ki so začetne točke trajektorij, ki se s časom približujejo atraktorju. Pomislimo kakšnih geometrijskih oblik vse so lahko atraktorji. V primeru dvo-dimenzionalnih tokov so to posamezne točke ali zaključene periodične krivulje, imenovane tudi limitni cikli. V tri-dimenzionalnih tokovih se naštetima primeroma lahko pridružijo še kvaziperiodične krivulje (primer je na sliki 1), kaj več pa si v naprej skoraj ne moremo zamisliti. Našteli smo le enostavne ali navadne atraktorje, pri tro ali več dimenzionalnih tokovih pa se lahko pojavijo tudi atraktorji z bolj zapleteno geometrijo. To so kaotični ali čudni atraktorji.
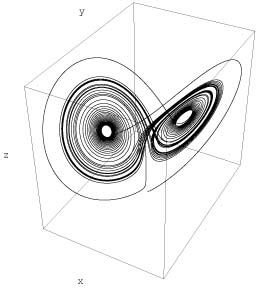
Slika1: (levo) Kvaziperiodična orbita. (desno) Lorenzov čudni atraktor.
V gibalnih enačbah, ki opisujejo razvoj sistema skozi čas, pogosto nastopajo različni sistemski parametri (masa, koeficienti vzmeti, dušenja in trenja, koeficienti sklopitve z vzbujanjem…). S spreminjanjem le teh lahko tudi kvalitativno spreminjamo dinamiko sistema. Take spremembe v dinamiki se imenujejo bifurkacije in se kažejo tudi kot spremembe lastnosti atraktorjev. Ko spreminjamo vrednost določenega sistemskega parametra se lahko zgodi, da se pri nekih določenih vrednostih parametra število atraktorjev podvoji ali pa da od te vrednosti naprej točka, ki je bila prej atraktor ni več atraktor. Lahko se torej rodijo novi atraktorji, se spremeni funkcijska odvisnost atraktorja od parametra, možna pa je tudi podvojitev periode limitnega cikla. Igra se lahko ponovi pri neki drugi vrednosti parametra, vendar se pri neki mejni vrednosti ustavi. Od tam naprej atraktor več ne ustreza nobenemu izmed prej omenjenih primerov. Gibanje na takem atraktorju je neurejeno–kaotično. Naš sistem je postal kaotičen in bližnje trajektorije v takem kaotičnem sistemu se s časom exponentno razhajajo, z dano časovno konstanto v določeni smeri. Neodvisnih smeri je toliko, kolikor dimenzionalen je fazni prostor. Razhajanje bližnjih trajektorij v neki smeri zapišemo z izrazom
kjer je d(0) razmik na začetku, d(t) je razmik po času t, časovno konstanto 
pa imenujemo eksponent Liapunova. Časovna konstanta razhajanja 
v smeri vzdolž trajektorije je enaka 0. V trodimenzionalnih tokovih preostaneta še dve časovni konstanti 
in 
, ki naj določata hitrost razhajanja trajektorij v dveh pravokotnih si smereh na ravnini, ki je povsod pravokotna na trajektorijo. Če naj se volumen faznega prostora V(t) okoli trajektorije s časom krči, mora biti vsota vseh časovnih konstant negativna, saj velja
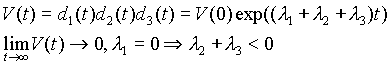
Od tod vidimo, da je kaotično gibanje v disipacijskih sistemih možno le kadar je tok tro ali več dimenzionalen, saj je = 0 in bi že v dvodimenzionalnem primeru edini še nedoločen moral zadoščati dvema izključujočima se pogojema: > 0, kar je lastnost kaotičnega gibanja. Čudni atraktor v tri dimenzionalnem faznem prostoru, si najlažje predstavljamo kot sloj neskončnega števila dvo-dimenzionalnih listov, ki se v faznem prostoru razteguje, guba in prelaga (slika 2a), nato pa se gladko sklene (slika 2c). Trajektorije na taki plasti se med sabo razhajajo in so hkrati omejene na ta objekt katerega dimenzija je manjša od dimenzije celega začetnega faznega prostora, vendar to ni kar ploskev, saj se trajektorije v faznem prostoru ne smejo sekati, kar pa bi se na ploskvi gotovo zgodilo. Zanimiv je prerez sloja. Listi so vloženi tako, da se vzorec na prerezih ponavlja pri vse manjših in manjših skalah (slika 2b). Tako zgradbo geometrijskega objekta imenujemo fraktalna zgradba ali fraktal.
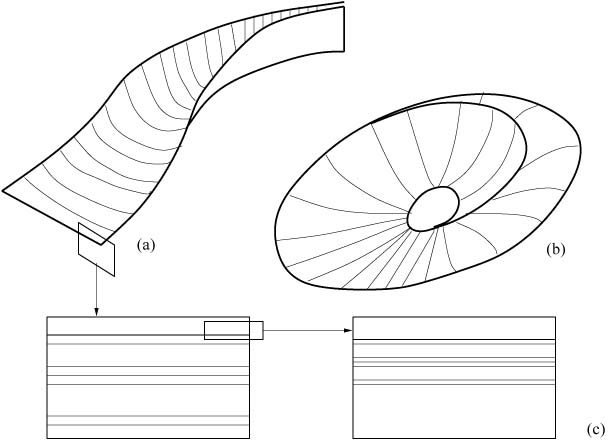
Slika2: Ilustracija čudnega atraktorja. (a) Raztegovanje in zgibanje, (b) gladka sklenitev, (c) fraktalna zgradba plasti atraktorja
