Naše telo je prilagojeno bivanju v določenem okolju; fizikalne količine, ki opisujejo to okolje (temperatura, tlak, težnost, sestava zraka, ki ga dihamo…), od svoje normalne vrednosti lahko odstopajo le do določene stopnje, če naj bo okolje še primerno za življenje. Kljub temu pa se nekateri čudaki včasih lotevamo dejavnosti v okoljih, ki niso običajna in ena izmed takšnih dejavnosti je potapljaštvo. Na kakšen način torej sprememba okolja pri potapljanju vpliva na potapljača in kako pod vodo uporabiti fiziko, da preživimo?
Osnove podvodne fizike

Najprej razčistimo: obstajata dva načina, kako se spustiti pod vodo in preživeti. Prvi je, da smo od okolja povsem ločeni, kakor v podmornici ali v potapljaškem “oklepu”, kakršnega se morda spomnimo iz Bondovega filma Samo za tvoje oči. V tem primeru nas sprememba tlaka ne zanima posebej, saj zanj skrbi jekleni oklep podmornice, mi pa dihamo tak zrak, kakor na kopnem. V drugem primeru – potapljanje na dah, s pomočjo jeklenke ali v potapljaškem zvonu – pa sprememba tlaka pod vodo vpliva na nas neposredno.
Karkoli že dihamo (navaden zrak ali kakšno drugo mešanico plinov), tlak plina, ki ga vdihnemo, mora biti približno ustrezen tlaku okolja, v katerem smo. Pljuča si namreč lahko predstavljamo kot nekakšen balon: če je tlak zraka, s katerim napolnimo balon, prevelik, se balon razpoči, če je premajhen, ostane balon prazen oziroma se skrči.
Na kopnem je zračni tlak približno konstanten in znaša na morski gladini 100 kPa (kilopaskalov), eno atmosfero ali en bar – vse to ustreza tlaku 10.000 kg / m2, kolikor znaša teža zraka nad nami. Voda je precej gostejša in zato težja od zraka: deset metrov vode tlak podvoji, tako da ta na globini desetih metrov pod morjem znaša 2 bara (200 kPa). Na vsakih deset metrov globine pa se tlak poveča še za en bar, kar opisuje formula za tlak:
p =ρ g h (Enačba 1)
p – tlak pod vodo
h – globina vode
ρ – specifična teža vode
g – težnostni pospešek
| globina | tlak vode |
| gladina | 1 bar |
| 10m | 2 bara |
| 20m | 3 bare |
| 30m | 4 bare |
| 100m | 11 barov |
Od tlaka pa je odvisen volumen (prostornina) plina in o tem govori prva za potapljače pomembna fizikalna zakonitost, Boylov zakon: pri konstantni temperaturi se volumen dane mase plina spreminja obratno sorazmerno z njegovim tlakom, ali
p V = konst. (Enačba 2)
p – tlak plina
V – volumen plina
Kaj to pomeni za naš balon oziroma pljuča? Predstavljajmo si, da balon na morski gladini, kjer je tlak 1 bar, napihnemo toliko, da njegov volumen znaša tri litre. Sedaj balon potopimo na globino desetih metrov, kjer tlak znaša 2 bara (tabela 1). Ker balon ni kakor notranjost podmornice ločen od okolja z jeklenim ščitom, temveč se prilagaja tlaku okolice, mora tudi tlak v balonu narasti na dva bara, kakršen je tlak okoli njega. Po Boylovem zakonu pa to pomeni, da se bo njegov volumen ustrezno (dvakrat) zmanjšal – balon bo uplahnil na polovico prejšnje prostornine.
Na površini: 1 (bar) krat 3 (litre) = 3 (konstanta za naš balon)
10 m pod vodo: 2 (bara) krat 1,5 (litra) = 3
Če naj po Boylovem zakonu produkt prostornine in tlaka našega balona ostane vselej konstanten, se mora pri povečanju tlaka iz enega na dva bara volumen balona zmanjšati za polovico! Poglejmo, kako se volumen trilitrskega balona po Boylovem zakonu spreminja pri potapljanju do 30 metrov:
| globina | tlak | volumen balona |
| gladina | 1 bar | 3 litre |
| 10 m | 2 bara | 1,5 litra |
| 20 m | 3 bare | 1 liter |
| 30 m | 4 bare | 0,75 litra |
Podobno kot balon se obnašajo naša pljuča. Pri potapljanju na dah bo, če bomo vdihnili na površini tri litre zraka, na dvajsetih metrih volumen tega znašal en liter, ko se bomo dvignili pa se bo spet povečeval do treh litrov. Ker potop traja kratek čas, to ne povzroča velikih težav, razen pri zelo globokih potopih, ko bi zaradi zmanjšanja volumna pljuč okolišnji tlak lahko zdrobil prsni koš.
Če hočemo pod vodo ostati daljši čas, pa moramo očitno dihati, kar nam omogoči zrak, ki ga sabo nesemo v jeklenki. Balon – pljuča – moramo torej napihniti pod vodo. Tretji stolpec tabele 2, ki opisuje manjšanje volumna zraka v pljučih pri potapljanju na dah, v tem primeru ne velja, saj moramo pri dihanju, ne glede na tlak, pljuča vselej napolniti do normalnega volumna, denimo treh litrov. Tudi pod povečanim tlakom bo volumen moral ostati isti – to pa pomeni, da bomo pri večjem tlaku za zapolnitev enakega volumna potrebovali več zraka, ki bo hkrati gostejši. Razmerje opisuje tale formula:
p V / m = konst. (Enačba 3)
p – tlak plina
V – volumen plina
m – masa plina
Izpeljemo jo iz plinske enačbe p V = n R T = (m/M) R T, če predpostavimo, da sta molska masa plina (isti plin) in temperatura konstantni. Podvodne posledice predstavimo v tabeli (zaradi majhne mase treh litrov zraka pri enem baru to namesto v kilogramih predstavimo kot eno enoto).
| globina | tlak | volumen balona | masa zraka |
| gladina | 1 bar | 3 litre | 1 enota |
| 10 m | 2 bara | 3 litre | 2 enoti |
| 20 m | 3 bare | 3 litre | 3 enote |
| 30 m | 4 bare | 3 litre | 4 enote |
Za potapljača, katerega zaloga zraka je omejena na tistega v njegovi jeklenki, je to kar pomembno: na globini tridesetih metrov bo namreč za en vdih porabil kar štirikrat več zraka, kakor na površini! Mimogrede, za to, da je zrak, ki ga diha potapljač, enakega tlaka kot okolišnji tlak pod vodo, skrbi naprava, imenovana regulator, ki stisnjen zrak (recimo 100 barov) iz jeklenke spravi na tlak, ki velja na določeni globini. Zgolj z dolgim šnorkljem, skozi katerega bi sesali zrak iz gladine, kjer je tlak 1 bar, na večji globini, kjer je tlak večji, ne bi mogli dihati.
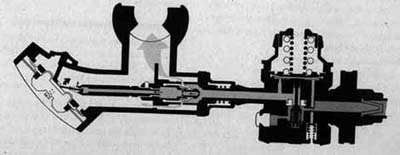
Učinki dihanja zraka pod tlakom
Zrak, ki ga dihamo, je mešanica različnih plinov. Za potapljača je še posebej pomembno, kako in zakaj povečan tlak zraka vpliva na njegovo telo.
Uvesti moramo nov pojem: zrak je mešanica plinov in ko govorimo o tlaku zraka, ki ga dihamo (pod ali nad vodo), je to tlak zmesi v celoti. Vendar pa ima vsak plin, ki sestavlja to zmes, svoj lastni, parcialni tlak, ki je manjši od tlaka zmesi v celoti. Seštevek vseh parcialnih tlakov plinov v zmesi da tlak celotne zmesi in o tem govori Daltonov zakon: tlak plinske mešanice je enak vsoti tlakov vsakega izmed plinov mešanice, če bi ta sam zavzemal ves volumen, ki ga zavzema mešanica.
p = p1 + p2 + p3 + … + pn (Enačba 4)
p – tlak zmesi plinov v celoti
pi – parcialni tlak posameznega plina
Plinska enačba za parcialni tlak posameznega plina:
pi = (mi/Mi) R V / T (Enačba 5)
M – molska masa plina (masa enega kilomola plina)
(Mdušik = 28 kg/kmol, Mkisik = 32 kg/kmol, Mzrak = 29 kg/kmol)
Če plinsko enačbo za parcialni tlak združimo z Daltonovim zakonom dobimo:
p = p1 + p2 + … + pn = (m1/M1 + m2/M2 + … + mn/Mn) R V / T (Enačba 6)
Naj bo xi odstotek posameznega plina v zmesi:
xi = mi/m (Enačba 7)
Iz Daltonovega zakona tako dobimo enačbo za parcialni tlak posameznega plina:
pi = (xi/Mi) Mzmesi p (Enačba 8)
p – tlak zmesi plinov v celoti
pi – parcialni tlak posameznega plina
xi – masni delež posameznega plina v zmesi
Mi – molska masa plina (masa enega kilomola plina)
Mzmesi – molska masa zmesi
Iz zgornje enačbe vidimo, da je parcialni tlak plina v zmesi sorazmeren njegovi odstotni zastopanosti v zmesi. Za primer si izračunajmo, kako se spreminja parcialni tlak kisika, ki ga je v zraku 21%, če se potapljamo z zrakom na globino 70 m.
| globina | tlak | parcialni tlak kisika |
| gladina | 1 bar | 0.19 bara |
| 10m | 2 bara | 0.38 bara |
| 40m | 5 barov | 0.95 bara |
| 70m | 8 barov | 1.52 bara |
Že pri štiridesetih metrih je torej tlak kisika v zraku takšen, kakor če bi na kopnem (pri enem baru) dihali čisti kisik! Z večanjem globine pa se še povečuje.
Parcialni tlak je za potapljača izrednega, takorekoč življenjskega pomena. Prav parcialni tlak nekega plina v mešanici namreč določa, kakšen učinek bo imel ta plin na potapljačev organizem. Kisik je na primer pri normalnem tlaku (0,19 bara) nujen za preživetje, pri tlakih nad 1,6 bara postane škodljiv, nad 2 bara pa je lahko celo smrtonosen! Zato potapljači pri potapljanju na zelo velike globine ne smejo uporabljati zraka, temveč mešanico plinov, v kateri je odstotek kisika manjši, kar po prej navedeni formuli kompenzira povečanje njegovega parcialnega tlaka.
Športni potapljači se običajno ne potapljajo v take globine, zato jim povečanje tlaka kisika ne povzroča težav. Drugače pa je z dušikom, ki ga je v zraku skoraj osemdeset odstotkov. Povečani tlak dušika je povezan z dvema največjima nadlogama, s katerima se srečujemo pri potapljanju: dušikovo omamo ali globinsko pijanostjo in dekompresijo. Vzrok globinske pijanosti je po najrazširjenejši razlagi narkotičen učinek dušika, ki se začenja pojavljati, ko znaša parcialni tlak dušika nad 4 bare – torej okoli štiridesetih metrov globine pri potapljanju z zrakom. Fiziološki vzroki tega še niso povsem razjasnjeni; helij jih na primer nima, kar je eden izmed razlogov, zakaj pri globokih potopih namesto zraka dihajo mešanico helija, dušika in kisika – trimix ali helija in kisika – heliox.
Da bi razumeli, kaj je dekompresija, pa moramo uvesti Henryjev zakon. Henryjev zakon pravi, da je pri dani temperaturi količina plina, ki se raztopi v tekočini, premo sorazmerna njegovemu tlaku. Ali z enačbo:
n*i = Ki pi(Enačba 9)
n* – količina plina, ki se raztopi v tekočini (recimo v molih na liter)
Ki – konstanta Henryjevega zakona, (konstanta za en plin in isto temperaturo)
pi – parcialni tlak plina
Vidimo, da se pri dvakrat povečanem tlaku (in nespremenjeni temperaturi) količina raztopljenega plina prav tako dvakrat poveča. Seveda pa velja tudi obratno: če se tlak zmanjša, se zmanjša količina plina, ki je lahko raztopljena v tekočini in ta plin se iz tekočine izloči – pojav, ki ga opazujemo, ko odpremo steklenico radenske: zaradi povečanega volumna se tlak zmanjša (Boyle), ogljikov dioksid, prej raztopljen v vodi, pa se izloči kot plin (mehurčki).
Poglejmo si sedaj potapljača, ki se z zrakom potopi na 40 metrov. Po enačbi za tlak (1) bo tu tlak zraka znašal 5 barov – štiri zaradi globine vode plus ena zaradi zračnega tlaka na površini. Iz Daltonovega zakona – dušika je v zraku 80% – po enačbi (8) izračunamo parcialni tlak dušika v tej globini (4 bare) in na površini (0.8 bara). Spomnimo se na Henryjev zakon (9) in izračunamo, da je količina dušika, raztopljenega v telesu (to je v glavnem iz tekočine) na globini štiridesetih metrov lahko kar petkrat večja kot na kopnem! Če bi se ta potapljač sedaj hitro dvignil na gladino, bi se dušik moral izločiti iz telesnih tekočin, kakor pri radenski, ko jo odpremo. V telesu bi nastali mehurčki dušika, ki bi resno poškodovali tkiva v telesu ali celo povzročili zastoj srca – potapljač bi zbolel za dekompresijsko boleznijo.
Na potapljačevo srečo vse le ni tako črno. Dekompresijski bolezni se lahko izogne, če upošteva določena dejstva, ki delujejo njemu v prid.
- Dušik se v telesu do svoje po Henryjevem zakonu maksimalne koncentracije ne nasiči kar takoj, ko se znajdemo pod vplivom povečanega tlaka. Koncentracija narašča s časom, ki ga tam preživimo in če ta čas ustrezno skrajšamo, omejimo tudi količino dušika, ki se raztopi v telesu.
- Telo lahko do določene mere izloča odvečni dušik, ki se sprosti ob dvigu iz globin, po neškodljivi poti, skozi pljuča. Če se dvigamo dovolj počasi, dušik ne bo tvoril mehurčkov, ki bi poškodovali telo, ampak se bo izločal skozi dihala.
- Če je ob dolgem in globokem potopu koncentracija dušika v telesu prevelika, jo lahko ob dvigovanju zmanjšamo z metodo dekompresijskih postankov. Dvignemo se do globine, ko je količina dušika, ki se sprošča, ravno še taka, da ne tvori mehurčkov, temveč se izloča skozi pljuča. Tam ostanemo toliko časa, dokler se koncentracija ne zmanjša do stopnje, ki je neškodljiva en globinski interval višje. Nato se dvignemo do te globine in tam postopek ponovimo glede na naslednjo višino dekompresijskega postanka. Tako počasi pridemo na površino.
Potapljaške tabele
Vsa ta dejstva, ob tem pa še fiziologija telesa, zaradi katere se iz različnih tkiv dušik izloča z različno hitrostjo, nam omogočijo konstrukcijo potapljaških tabel, iz katerih razberemo varen čas zadrževanja v globini, čas dvigovanja in potrebne dekompresijske postanke – torej pogoje za varen potop.
Dva primera potapljaških tabel iz knjige Ronjenje u sigurnosti Stracimira Goševića:
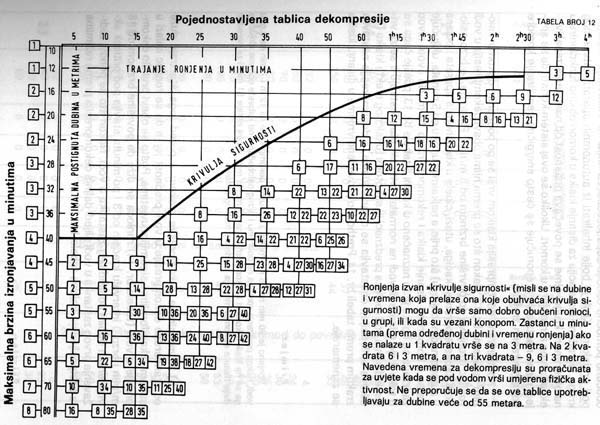
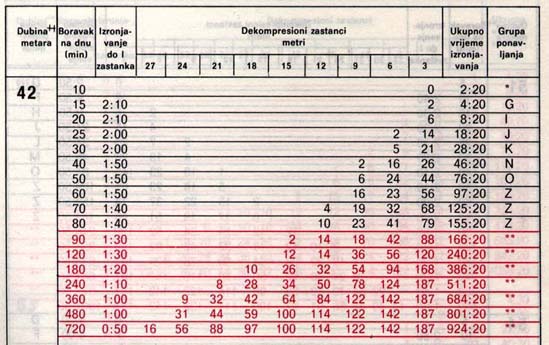
Nekaj zanimivih spletnih strani:
- Scuba Diving Explained – Odlična on-line knjiga o potapljanju!
- Revija DIVER Magazine; testi potapljaške opreme
- Potapljaška zveza PADI
- Društvo za Raziskovanje Morja
- Fiziologija za potapljače
(Luka Omladič, kvarkadabra.net – št. 2, december 1999)

















