Predpostavimo, da v nekem trenutku izmerimo lego kvantnega delca (elektrona, fotona, protona…), in ugotovimo, da se nahaja v točki X. Zanima nas, kje je bil delec samo trenutek pred našo meritvijo? Možnih je več odgovorov: a) Delec je bil v točki X. b) Delca ni bilo pravzaprav nikjer. c) Odgovora na to vprašanje ni. V članku bomo poskušali pokazati, da izidi nekaterih novejših poskusov podpirajo le odgovor b, da delca ni bilo pravzaprav nikjer. Beri in se čudi!
Albert Einstein gotovo ne bi bil navdušen nad izidom eksperimenta, ki so ga leta 1997 izvedli fiziki univerze v Ženevi, nedaleč stran od patentnega urada, v katerem je davnega leta 1905 spisal nekaj svojih najpomembnejših člankov. Poleg posebne teorije relativnosti je tistega leta objavil tudi razlago fotoefekta, ki je temeljila na kvantni naravi svetlobe. V tej razlagi je postavil temelje za nastanek teorije kvantne mehanike, z interpretacijo katere se kasneje nikakor ni mogel strinjati. Prepričan je bil namreč, da kvantna mehanika v obliki, kot so jo poznali takrat – vendar danes ni kaj dosti drugače -, ne opiše narave dovolj podrobno, da bi bili lahko z njo zadovoljni. Poskus skupine z univerze v Ženevi pod vodstvom Nicolasa Gisina pa je ponovno dokazal, da so bili Einsteinovi ugovori bolj plod osebnega vere v realistični koncept narave kot bistroumen uvid v skrivnosti njenega obnašanja.
Raziskovalna skupina z univerze v Ženevi je na posodobljen način izvedla Einsteinov miselni poskus, s katerim je pred 60 leti poskušal dokazati, da kvantna mehanika nikakor ni skladna s posebno teorijo relativnosti. Za izvedbo poskusa so uporabili nekaj telefonskih optičnih kablov, ki povezujejo mesto z okoliškimi vasmi, in jih uporabili kot vodila, po katerih so potovali fotoni. Da bi razumeli, kaj so švicarski fiziki pravzaprav sploh merili, se moramo najprej malo razgledati po okolici in se spoznati z zanimivimi dogajanji v svetu kvantov.
Kje je bil delec trenutek pred meritvijo?
“Verovanje v zunanji svet, ki je neodvisen od opazujočega subjekta, je temelj naravnih znanosti.” (Albert Einstein)
Predpostavimo, da v nekem trenutku izmerimo lego kvantnega delca (elektrona, fotona, protona…), in ugotovimo, da se nahaja v točki C. Zanima nas, kje je bil delec samo trenutek pred našo meritvijo. Navedli bomo tri smiselne odgovore, ki so hkrati tudi trije osnovni pogledi na interpretacije dogajanja v kvantnem svetu.
- Realistični pogled: Delec je bil v točki C. Zagovornik te klasično zdravorazumske interpretacije je bil med drugimi tudi Einstein. Na videz je realistični odgovor povsem sprejemljiv, vendar pozor: če sprejmemo to trditev, iz nje nujno sledi, da je kvantna mehanika nepopolna teorija, saj ne zna napovedati resnične lege delca, čeprav narava to v načelu dopušča. Za realista naše nepoznavanje točne lege delca ni posledica zakona narave, ampak zgolj naše nevednosti. Lega delca ni nikoli nedoločena, je le nepoznana. Zato valovna funkcija delca ne opiše v celoti. Poleg nje potrebujemo za popolni opis delca še (nam) skrite , nepoznane količine.
- Ortodoksni pogled: Delca ni bilo pravzaprav nikjer. Sama meritev je šele prisilila delec, da se je odločil za eno izmed leg. (Zakaj se je med vsemi možnostmi odločil ravno za točko C, raje ne sprašujmo.) Kot je rekel eden izmed avtorjev kvantne teorije, Pascual Jordan: “Meritev ne le zmoti, kar želimo opazovati, temveč to pravzaprav šele ustvari… Delec z meritvijo prisilimo, da zavzame eno od leg.” Oče tega pogleda (tako imenovane copenhagenske interpretacije) je Niels Bohr s svojimi sodelavci. Med fiziki je bil ortodoksni pogled vedno najbolj razširjen in splošno sprejet, ker je bil dokaj uporaben tudi v praksi. Pri običajnih poskusih po navadi ne opazujemo posameznih delcev, ampak skupine z nekaj milijoni članov. Takrat nas zanimajo predvsem povprečne vrednosti količin za takšno skupino, kar zna kvantna mehanika z ortodoksno interpretacijo dovolj dobro pojasniti in napovedati. Težave se pojavijo šele pri obravnavi posameznih delcev. Vendar ne pozabimo, da če je takšna interpretacija resnična, je v dejanju meritve nekaj zelo čudaškega – nekaj, kar se v polstoletni debati ni niti malo razjasnilo.
- Agnostični pogled: Odgovora na to vprašanje ni. Takšno stališče sploh ni tako absurdno, kot se na prvi pogled mogoče zdi. Navsezadnje, kakšen smisel ima postavljati izjave o položaju delca, preden je bila meritev sploh izvedena, če je edini način, kako se lahko prepričamo o resničnosti naših domnev, le izvedba meritve? Na takšen način pa zmeraj dobimo le informacijo o stanju delca po meritvi. Kaj ni ukvarjanje s pojavi, ki jih po svoji naravi ne moremo empirično opazovati nekaj, kar ne spada več v fiziko? Wolfgang Pauli je nekoč izjavil: “Možganov nima smisla mučiti z mislimi o eksistenci nečesa, o čemer nikoli ne bomo mogli vedeti nič gotovega, nič bolj, kot s starim sholastičnim problemom, koliko angelov lahko sedi na konici igle.” Več desetletij je bil agnostični pogled bolj zasilno stališče fizikov v neskončnih razpravah o vprašanju: “Kako razumeti kvantni svet?” V pogovoru so poskušali najprej prodati odgovor 2, če pa je bil sogovornik preveč vztrajen, so preprosto preskočili na odgovor 3 in zaključili dialog.
Vsi trije pogledi (realistični, ortodoksni in agnostični) so imeli dolgo vsak svoje vnete zagovornike, dokler ni leta 1964 John Bell sveta osupnil s presenetljivo hipotezo. Predvidel je poskus, s katerim bi lahko prišli do merljive razlike med obnašanjem delca, ki ima točno določeno (čeprav nam nepoznano) lego pred meritvijo, in delca, ki si šele med meritvijo izbere lego. Bellovo odkritje je iz boja za prevlado odstranilo agnostično pozicijo, izbor med 1 in 2 pa prepustilo dovolj dobro izvedenemu eksperimentu.
Paradoks EPR
“Čudovite ideje imajo mladi dandanes. Vendar ne verjamem niti besede.” (Albert Einstein po Heisenbergovem predavanju o načelu nedoločenosti leta 1927)
Leta 1935 so Einstein, Podolsky in Rosen objavili članek, v katerem so poskušali z miselnim poskusom dokazati, da je realistični pogled edino konsistentno stališče o dogajanju v kvantnem svetu. Njihov poskus si bomo ogledali v malo poenostavljeni verziji, ki jo pripisujejo Davidu Bohmu.
Pion $latex \pi ^{0}$ z nevtralnim električnim nabojem razpade v elektron in pozitron:

Elektron in pozitron odletita v nasprotnih smereh (slika 1). Ker je imel pion spin 01, spin pa je količina, ki se pri razpadu delcev ohranja, morata enak spin obdržati tudi oba novo nastala delca skupaj. Posamezen elektron (pozitron) ima sicer spin 1/2, vendar lahko dva delca skupaj sestavita tudi stanje s spinom 0. To je mogoče le v primeru, ko imata njuna spina nasprotni smeri. Pozitron ima npr. spin, usmerjen navzgor, elektron pa navzdol, ali obratno. Teorija kvantne mehanike ne zna napovedati, kako bo usmerjen spin posameznega delca, napove le, da bosta imela delca nasprotno usmerjene spine. Predpostavimo sedaj, da novo nastala delca odletita daleč vsak v svojo smer (lahko tudi nekaj svetlobnih let stran), nato izmerimo spin elektrona. Recimo, da ima spin navzgor. S to meritvijo smo v istem trenutku določili tudi spin pozitrona, ki je daleč stran.
Za realista ni to nič presenetljivega, saj je prepričan, da sta imela elektron in pozitron točno določeno smer spina že od nastanka naprej, problem je le, da kvantna mehanika tega ni znala napovedati. Za pristaša ortodoksnega pogleda pa delca nista imela določenega spina do samega trenutka meritve. V trenutku meritve se je posamezen delec šele odločil, kakšen spin bo imel. Tako je meritev spina na elektronu povzročila, da je točno določeno smer spina (ravno nasprotno) dobil tudi pozitron nekaj svetlobnih let daleč. Ker pa teorija relativnosti prepoveduje potovanja s hitrostmi večjimi od svetlobne, pride tu do teorijskega kratkega stika. Einstein je takšno interpretacijo poskusa imenoval “fantomsko delovanje na daljavo” (spooky action-at-a-distance) in jo imel za absurdno. Iz miselnega poskusa je sklepal, da je ortodoksni pogled napačen in kvantna teorija nepopolna.
Paradoks EPR (Einstein, Podolsky in Rosen) temelji na predpostavki, da se nič ne more gibati hitreje kot svetloba, kar se v žargonu imenuje načelo lokalnosti. Ortodoksni pogled in načelo lokalnosti nista združljiva, ker bi teoretično lahko (če med delcema ni izmenjave informacij (lokalnost) in spin ni vnaprej določen (ortodoksna interpretacija)) npr. hkrati izmerili obema delcema spin navzgor, kar bi kršilo zakon ohranitve spina, česa podobnega pa še nikoli niso opazili.
Bellova neenakost
“Vsakdo, ki ga kvantna fizika ni pretresla, je ni razumel.” (Niels Bohr)
Einstein, Podolsky in Rosen niso trdili, da kvantna mehanika ni dobra fizikalna teorija, ki ne bi znala pravilno napovedati dogajanja v naravi. Dokazati so poskušali le, da (še) ne da popolnega opisa narave. Verjeli so, da poleg valovne funkcije obstaja še neka skrita količina, s poznavanjem katere bi lahko vsak naravni sistem opisali v celoti in do potankosti točno predvideli njegovo prihodnost, če bi le poznali tudi zakone, po katerih se spreminja. Količina ima pridevnik skrita, ker se (skoraj) nikomur ne sanja, kako bi z njo računali ali jo merili.
John Bell je predlagal posplošitev EPR/Bohmovega miselnega poskusa: Namesto fiksne postavitve merilcev elektronovega in pozitronovega spina je predlagal vrtljive merilce, ki bi jih lahko zavrteli v poljubno smer okoli osi gibanja elektrona. Najprej bi merili komponento elektronovega spina v smeri npr. vektorja a, kar z drugimi besedami pomeni, da bi detektor zasukali v smer a. Podobno bi detektor za spin pozitrona zasukali v smer b (slika 2). Da bo bolj enostavno, vzemimo za enoto meritve spina kar \hbar/2. Vsak detektor lahko registrira pri prehodu elektrona ali pozitrona le dve možnosti: +1 za spin gor in -1 za spin dol v smeri detektorja. Tabela zapisov meritev za več zaporednih razpadov \pi ^{0} bi lahko izgledala takole:
| elektron | pozitron | produkt |
| -1 | +1 | -1 |
| +1 | +1 | +1 |
| +1 | -1 | -1 |
| +1 | +1 | +1 |
| -1 | -1 | +1 |
| … | … | … |
Iz meritev nato izračunamo povprečje produkta spinov za dano orientacijo detektorjev, in novo količino imenujmo P(a,b). Za primer, ko sta vektorja a in b enaka (a = b), dobimo staro EPR različico eksperimenta. Tu je ena meritev zmeraj +1, druga pa -1, kar vedno pripelje do produkta -1, zato je povprečje:
P(a,a) = -1
Antiparalelna detektorja (a = –b) imata iz podobnih razlogov zmeraj produkt +1, zato:
P(a,-a) = +1
Za poljubno orientacijo spinov teorija kvantne mehanike napove povprečje:
P(a,b) = –aˇb
Pri tem predstavlja pika med a in b skalarni produkt vektorjev. Bell je dokazal, da je takšen rezultat nemogoč za vsako lokalno teorijo s skritimi spremenljivkami. Podrobni izpeljavi tu ne bomo sledili, orisali bomo samo nekaj najpomembnejših elementov.
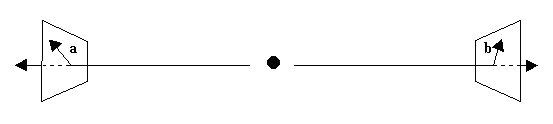
Predpostavimo, da je za “popoln” opis sistema elektrona/pozitrona potrebna vpeljava nove skrite spremenljivke q. Le-ta se na nam nepoznan način spreminja od enega razpada piona do drugega. Naprej predpostavimo, da je izid meritve na elektronu neodvisen od orientacije (b) detektorja za pozitron, ki ga eksperimentator lahko izbere šele tik pred vstopom pozitrona v detektor, tako da se zaradi končne hitrosti potovanja informacij (omejitev s svetlobo hitrostjo) detektorja med seboj ne moreta uskladiti – predpostavka lokalnosti. Ker poznamo skrito spremenljivko, lahko točno napovemo izid meritve spina na elektronu A (a,q) in na pozitronu B(b,q). Obe napovedi lahko zavzameta le vrednosti +-1.
S pomočjo krajšega računa je prišel Bell do ugotovitve, da velja za lokalno teorijo s skritimi spremenljivkami naslednja neenakost, ki je danes znana pod imenom Bellova neenakost:
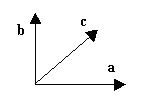
![]() Že bežen premislek pa nam pove, da napoved običajne kvantne mehanike (P(a,b) = -a(b) krši Bellovo neenakost. Poglejmo primer treh orientacij za oba detektorja, ki so zamaknjene za kot 45( (slika 3). Kvantna mehanika zanje napove povprečja meritev:
Že bežen premislek pa nam pove, da napoved običajne kvantne mehanike (P(a,b) = -a(b) krši Bellovo neenakost. Poglejmo primer treh orientacij za oba detektorja, ki so zamaknjene za kot 45( (slika 3). Kvantna mehanika zanje napove povprečja meritev:
P(a,b) = 0, P(a,c) = P(b,c) = -0.707
To očitno krši zgornjo neenakost:
Z Bellovo modifikacijo postane trditev paradoksa EPR še veliko bolj radikalna, kot so si predstavljali njegovi avtorji leta 1933. Če bi njihova kritika držala, potem kvantna mehanika ne bi bila le nepopolna, ampak sploh napačna. Mogoče je seveda tudi nasprotno razmišljanje, če je kvantna mehanika resnična, potem nas tudi teorije skritih spremenljivk ne bodo obvarovale pred “fantomskim delovanjem na daljavo”, ki je tako motilo Einsteina. Vprašanje, kdo ima prav, pa lahko razreši že dokaj preprost poskus.
Ekperimentalno testiranje Bellove neenakosti
“Sumim, da vesolje ni le bolj čudno, kot si predstavljamo, ampak bolj čudno, kot si sploh lahko predstavljamo.” (John B. S. Haldane, britanski genetik)
V 60. in 70. letih je več raziskovalnih skupin poskušalo testirati Bellovo neenakost. Raziskave so dosegle vrh v delu Aspecta, Grangiera in Rogerja v začetku 80. let. Čeprav se ne bomo spuščali v podrobnosti, omenimo le, da so namesto para elektron-pozitron v poskusu uporabili dva korelirana fotona, detektorje pa so usmerili v naključno smer šele, ko sta bila fotona že na poti. Rezultati so se skladali z napovedjo kvantne mehanike in kršili Bellovo neenakost.
Eksperimentalna potrditev kvantne mehanike pa je – na prvi pogled mogoče nenavadno – šokirala večino znanstvene javnosti. Vendar ne zato, ker je ovrgla realistični koncept realnosti – večina fizikov se je na čudnost kvantne mehanike že privadila in tudi vrata za realistične nelokalne teorije s skritimi spremenljivkami so bila še zmeraj odprta, saj Bellova neenakost odstrani le lokalne teorije. Pravi šok je predstavljalo spoznanje, da je sama narava v sebi nelokalna. Do Aspectovih poskusov je bila ortodoksna interpretacija trenutnega sesutja valovne funkcije ob meritvi (v našem primeru uskladitev orientacije spinov med elektronom in pozitronom) razumljena bolj kot nekakšen artefakt formalizma brez opazljivih oziroma merljivih posledic. Danes takšni izmuzljivi odgovori ne zdržijo več.
Hitrosti večje od svetlobne
“Bog ne le kocka, ampak včasih vrže kocko tudi tako, da se je ne da videti.” (Stephen Hawking)
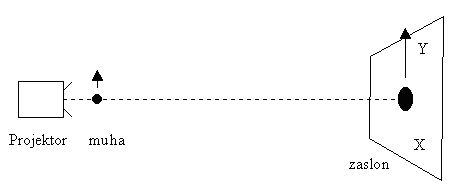
Zakaj je fizike ideja o vplivih, hitrejših od svetlobe, sploh tako razgrela? Ali ni v naravi veliko pojavov, pri katerih nekaj potuje hitreje od svetlobe? Če leti muha pred objektivom diaprojetorja, je hitrost potovanja njene sence po platnu sorazmerna z razdaljo do platna. Če je lahko razdalja poljubno velika, se teoretično senca lahko giblje poljubno hitro (slika 4). Vendar senca ne nosi nobene energije in tudi informacije ne more posredovati iz enega konca platna na drugega. Človek na mestu X nikakor ne more deformirati sence tako, da bi lahko vplivala na mesto Y.
Potovanje informacij z nadsvetlobno hitrostjo bi namreč po predvidevanjih posebne teorije relativnosti informacije pošiljalo nazaj v času. Tako bi lahko povzročilo učinek pred samim vzrokom, kar bi privedlo do logičnih paradoksov, kot so umor lastnih prednikov, preden so nas ti sploh spočeli. In v katero skupino nadsvetlobnih gibanj sodijo nelokalni vplivi v kvantni mehaniki? Ali so, podobno kot sence, nesposobni prenašati informacije ali pa obstaja možnost za vplivanje na preteklost?
Vrnimo se nazaj k Bellovemu poskusu. Zanima nas, ali meritev na elektronu vpliva na obnašanje pozitrona? Kot smo videli zgoraj, sta obe meritvi med seboj usklajeni, torej takšen vpliv obstoji. Vendar, ali lahko iz tega sklepamo, da lahko preko nelokalnosti prenašamo informacije? Nikakor ne, saj smeri spina na elektronu, npr. spin gor, ne moremo poljubno nastaviti. Za lažje razumevanje si pomagajmo s preprosto analogijo. Kocko, za katero vemo, da ima vsoto pik na nasprotnih straneh zmeraj 7 (1-6, 2-5, 3-4), mečemo po stekleni mizi. Opazovalec, ki je pod mizo, bo iz številke, ki jo vidi s spodnje strani, brez težav izračunal, koliko pik smo vrgli, vendar mu na tak način ne moremo posredovati nikakršnega sporočila. Informacijo bi mu prenesli le v primeru, če bi lahko kocko zavestno postaviti na številko, ki bi imela vnaprej določen pomen. To pa ni dopustno ne pri kockanju in ne pri meritvah na kvantnih delcih. Usklajenost med meritvami opazimo šele, ko primerjamo seznama obeh meritev pri elektronu in pri pozitronu, do takrat so spiski meritev le seznami naključnih števil.
Poskusimo ugotovitve strniti v tabeli:
| Velja kvantna mehanika brez skritih spremenljivk. | Kvantna mehanika ni popolna teorija, ker ne poznamo vseh skritih količin. | |
| Teorija krši načelo lokalnosti. | Načeloma mogoče. | Načeloma mogoče. |
| Velja načelo lokalnosti. | Kršili bi nekatere osnovne ohranitvene zakone fizike. | Ovrženo s poskusi, ki temeljijo na Bellovi neenakosti. |
Kako naprej?
“Zdravi razum ni nič drugega kot skupek predsodkov, ki se naberejo v možganih pred osemnajstim letom starosti.” (Albert Einstein)
Skupina fizikov univerze v Ženevi z začetka naše pripovedi je testirala Bellovo neenakost na fotonih, podobno kot Aspect pred 15 leti, le da so razdaljo med detektorji povečali iz Aspectovih nekaj metrov na 10 km. Rezultati novega poskusa se niso bistveno razlikovali od primera, ko sta bila detektorja blizu skupaj. Kot vse kaže, je narava res nelokalna. Vendar Grisim z rezultati še ni popolnoma zadovoljen. Želi si, da bi testiral nelokalnost na še večji razdalji. Mogoče kar na 100 km, med Ženevo in Bernom kjer je imel sedež patentni urad, v katerem je uradoval Einstein. Tudi datum poskusa je že izbral: leto 2005, točno sto let po objavi Einsteinovih pionirskih odkritij.
Opombe:
1 Spin je vrtilna količina delca, ki ni posledica vrtenja. Sprva so mislili, da je spin posledica sukanja delca okrog svoje osi, a so že kmalu izračunali, da bi se morala po tej predstavi površina delca gibati hitreje od svetlobe, to pa ne gre. Spin danes razumemo – podobno kot maso in naboj – kot notranjo lastnost delca.
kvarkadabra.net – številka 5 (junij 2000)

















Zanimivo!