|
Je res, da se Zemlja jeseni hitreje vrti? Vzrok naj bi bil v dejstvu, da je več listopadnega gozda na severni polobli. Ko jeseni listje odpade, se celotna biomasa listja približa središču zemlje (osi) za višino drevesa. Kolikšna sploh je ta biomasa? Morda bi teoretični izračun na sedemindvajset decimalk to potrdil. Ali bi ga bilo možno preveriti tudi z meritvami?? |
kvarkadabra.net |
Če smo zelo natančni, to celo drži. Za lažjo predstavo si prikličimo v spomin umetnostno drsalko pri izvajanju piruete. Le ta se začne vrteti hitreje, ko da roke k telesu ali pa jih dvigne nad glavo v samo os vrtenja. Podobno bi se tudi Zemlja vrtela hitreje, ko bi listje padlo bližje k osi vrtenja Zemlje. Razložimo vse skupaj še z več fizikalnega besednjaka: vrtilna količina L se ohranja, če ni zunanjih navorov. Vrtilna količina pa je produkt vztrajnostnega momenta J in kotne hitrosti , ki nam poda za koliko se zavrti telo v eni sekundi (merjeno v radianih)
L=J
Vztrajnostni moment nekega telesa je tem večji, večja kot je njegova masa, ter dlje kot sega od osi vrtenja. Za valj, ki se vrti okoli svoje osi je npr.
J=mr2/2
Če na telo ne deluje navor, se vrtilna količina ohranja. Če se spremeni vztrajnostni moment telesa, se mora tako spremeniti tudi kotna hitrost. Če se npr. Zemlji vztrajnostni moment zmanjša (listje pade bližje osi vrtenja), se mora Zemlja hitreje vrtet. Vendar pa je problem pri sistemu Zemlja-listje ta, da je sprememba resnično majhna. Za šalo jo poizkusimo oceniti. Kot najbolj ekstremno možnost vzemimo, da je Zemlja prekrita enakomerno z gozdom (kar seveda ni res, še posebno, ker je nekako 3/4 površine Zemlje prekrite z oceani). V tem gozdu naj raste v povprečju eno drevo na kvadratni meter (kar je zelo na gosto). Kot oceno vzemimo, da ima vsako tako drevo tono listja, visoko pa naj bo v povprečju okoli 10m. Od tu lahko izračunamo, da bi v takem gozdu bilo za okoli 1017 kg listja, kar je seveda zelo veliko, a zopet ne tako zelo, če to številko primerjamo z maso Zemlje mZ=5.9 1024 kg. Tudi naš povsod se raztezajoči gozd, bi predstavljal le okoli 10 milijardin Zemljine teže. Seveda je v resnici gozda na Zemlji še veliko manj, ter je ustrezna masa listja prav gotovo kar nekaj velikostnih razredov manjša od naše ocene.
In kolikšen bi bil vpliv na gibanje Zemlje, če bi vso listje padlo na površino Zemlje z višine 10m? V tem primeru bi se vztrajnostni moment Zemlje spremenil za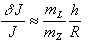 
kjer je 
relativna sprememba vztrajnostnega momenta Zemlje, J je vztrajnostni moment Zemlje na začetku, mL je masa listja, mZ masa Zemlje, h višina s katere pade listje in R radij Zemlje, ki je okoli 6400 km. Za višino h=10m tako dobimo ~10(-13). Tolikšna je potem tudi sprememba kotne hitrosti (hitrosti vrtenja). Tudi ob tako gostem gozdu, kot smo si ga zamislili v gornjem primeru, bi se sprememba kotne hitrosti poznala šele na trinajstem decimalnem mestu, v resničnem življenju bi bila tako še toliko manjša. Še posebno, ker moramo upoštevati, da je le del drevja listopadnega, saj to raste večinoma le v zmernem klimatskem pasu, medtem ko na severu prevladujejo iglavci, ob ekvatorju pa eksotično rastje. Veliko večji vpliv na vrtenje Zemlje bi lahko pripisali gibanju zračnih in vodnih mas, a tudi tu lahko ocenimo da se vpliv ne pokaže prej kot na desetem decimalnem mestu. Za kakšna eksperimentalna opazovanja na žalost ne vem, takole na pamet pa bi dejal, da so zelo težavna, saj bi morali vključiti še vse ostale vplive, npr. gravitacijski vpliv sosednjih planetov in Lune, verjetno pa tudi sončni veter ipd.
