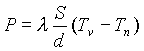| Ali obstaja povezava med toplotno prevodnostjo snovi in njihovo specifično toploto? |
Že intuitivno lahko pričakujemo, da bo toplotna prevodnost snovi v taki ali drugačni zvezi s specifično toploto. Toplotna prevodnost namreč govori o tem, kako uspešno lahko snov prenaša toploto od toplejšega dela k hladnejšemu. Specifična toplota pa nam pove za koliko se segreje snov, ko ji dovedemo toploto.
Zvezo torej lahko pričakujemo vsaj v nekaterih primerih, a najprej si oglejmo definiciji za obe količini. Imejmo tako ploščo iz snovi katere toplotna prevodnost nas zanima. Ena stranica plošče naj bo na višji temperaturi Tv, druga pa na nižji temperaturi Tn. Tedaj bo tekel toplotni tok P od stranice z višjo temperaturo k stranici z nižjo temperaturo
Sorazmernostni faktor 
je koeficient toplotne prevodnosti. A kako se toplota na mikroskopskem nivoju prenaša po snovi? Najlažje si to pojasnimo na primeru idelanega plina. Tu je kinetična energija molekul premo sorazmerna temperaturi plina; višja kot je temperatura plina, višja je energija molekul. Če torej plin na eni strani segrevamo, bodo molekule plina imele v povprečju višjo kinetično energijo. Preko trkov jo bodo oddajale molekulam v okolici, imeli bomo torej tok kinetične energije (toplote!) od mesta z višjo temperaturo (povprečno energijo molekul) k mestu z nižjo temperaturo (povprečno energijo molekul).
In kolikšen bo ta prenos energije? Saj se še spomnimo enačbe iz srednješolske fizike, ki pravi, da je prejeta toplota pri konstantnem volumnu sorazmerna spremembi temperature telesa
Q=m cv (Tkončna-Tzačetna)
kjer je m masa telesa in cv specifična toplota snovi? Molekula, ki bo priletela od vročega dela k hladnejšemu, bo s trkom oddala energijo drugi molekuli na mestu z nižjo energijo, prenešena kinetična energija pa bo v povprečju sorazmerna razliki obeh temperatur- sorazmernostni koeficient je specifična toplota cv (pomnožena še z maso molekule). V povprečju bo pač kinetična energija, ki jo izgubi molekula ob trku, enaka zgoraj zapisani enačbi za Q. Upoštevati moramo le še pogostost trkov (kar zahteva le malce podrobnejšo obravnavo, ki pa se je tu ne bomo lotili) in že dospemo do zveze med toplotno prevodnostjo in specifično toploto za idealni plin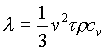
kjer je v2 povprečni kvadrat hitrosti molekule v plinu,
gostota plina, 
pa povprečni čas med trkoma. Kot se zdi formula preprosta, pa zgornja zveza ne daje vedno preproste zveze med specifično toploto in toplotno prevodnostjo, saj je izračun povprečnega časa med dvema trkoma lahko kaj zahteven računski problem.
Zanimiva je na primer ocena toplotne prevodnosti pri izolatorjih. Tu nosijo večino notranje energije različna nihanja ionov v kristalni mreži izolatorja. Različnim nihajnim načinom pripadajo v kvantnem opisu nihanj kvanti energije- fononi. Le ti se obnašajo kot neke vrste kvazi delci, ki jih lahko opisujemo skoraj kot idealni plin. Za izolatorje bo torej veljala gornja zveza med specifično toploto in toplotno prevodnostjo. Težko je le oceniti povprečni čas med trkoma. Le ta bo odvisen od notranjih lastnosti kristala (razporeditve molekul v kristalni mreži in posledično električnih polj v katerih ležijo posamezni atomi) pa tudi ostalih lastnosti posameznega vzorca, kot so število nečistoč na katerih se sipljejo fononi, pa tudi velikost in oblika posameznega vzorca, saj se bo, če ne prej, fonon odbil na stenah vzorca. Ko nižamo temperaturo vzorcu izolatorja se intrinzičen čas med trkoma podaljšuje ekponento. Pri dovolj nizki temperaturi tako doseže intrinzični čas med trkoma čas, ki ga fononi potrebujejo, da prepotujejo cel vzorec in se sipljejo na stenah. Pri zelo nizkih energijah, bo torej odvisen le od velikosti in oblike vzorca in nič več od temperature. Tedaj je toplotna prevodnost odvisna le še od specifične toplote izolatorja. Ta pa se, kot kaže račun, spreminja pri nizkih temperaturah s temperaturo kot T3.
Teoretične ugotovitve potrjujejo tudi eksperimentalni izsledki. Kot kaže slika, najprej toplotna prevodnost narašča s padajočo temperaturo, pri čemer je toplotna prevodnost neodvisna od velikosti vzorca. Nato doseže maksimalno vrednost, nakar pada s padajočo temperaturo, in sicer sorazmerno s specifično toploto snovi. Toplotna prevodnost in s tem sorazmerni koeficient je pri tem odvisna od velikosti in oblike vzorca ( je pač odvisen od velikosti in oblike vzorca, a neodvisen od temperature). Ravno to tudi napove teorija. Iz zveze za idealni plin, ki smo jo zapisali zgoraj, preberemo, da se v primeru, ko je neodvisen od temperature (primer izolatorja pri nizkih temperaturah), toplotna prevodnost s temperaturo spreminja tako kot specifična toplota
. 
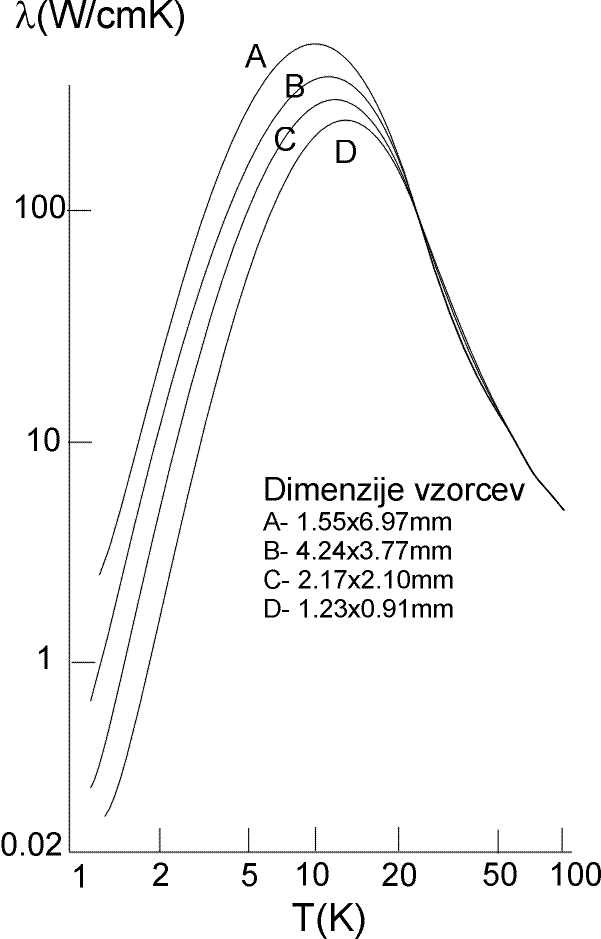
Slika1: Temperaturna odvisnost toplotne prevodnosti za kristal LiF. Pod nekako 10K toplotno prevodnost določa velikost vzorca (za razlago glej tekst)!
Še bolj zanimiva je zgodba s toplotno prevodnostjo in specifično toploto pri kovinah. Tu imamo za razliko od izolatorjev dva prispevka. Tako kot pri izolatorjih imamo fononski prispevek, poleg njega pa še prispevek elektronov v prevodnem pasu kovine (tega prispevka pri izolatorjih ni, ker je elektronov v prevodnem pasu premalo- od tu tudi slaba prevodnost izolatorjev). Kleč tiči v tem, da k toplotni prevodnosti največ prispevajo prevodni elektroni, medtem ko specifično toploto pri sobnih temperaturah določa skoraj povsem le fononski prispevek. Zaradi tega pri kovinah ni neposredne zveze med toplotno prevodnostjo in specifično toploto. Pač pa sta že leta 1853 Wiedeman in Franz opazila, da je produkt specifične toplote in specifične upornosti sorazmeren temperaturi, pri čemer je sorazmernostni koeficient neodvisen od vrste kovine. Ta empirični Wiedeman-Franzov zakon je prvi “pojasnil” Drude s teoretičnim modelom kovine, kjer je elektrone obravnaval kot idealen klasični plin. Za zvezo je dobil
,
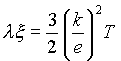kjer je k=R/NA Boltzmannova konstanta, 1.38 10-23J/K. Sorazmernostna konstanta med produktom toplotne prevodnosti in specifične upornosti 
je bila le dvakrat manjša od izmerjene vrednosti. Ta uspeh je v prejšnjem stoletju sprožil veliko zanimanja za Drudejev model kovine. A kaj, ko je bil uspeh Drudejevega opisa le navidezen. Prispevka elektronov k specifični toploti namreč z eksperimentom nikakor niso mogli potrditi. Razlog je bil seveda v tem, da prispevek elektronov k specifični toploti kot že rečeno zakriva veliko večji fononski pripsevek. Pri Drudejevem računu je bilo tako v igri nekaj naključij. Pravi kvantnomehanski račun namreč pokaže, da je elektronski prispevek k specifični toploti okoli 100krat manjši kot da klasični račun, medtem ko je povprečna hitrost elektronov okoli 100krat večja. Oba popravka se krajšata, tako da je kvantnomehanski rezultat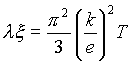
,
le za faktor 2 večji od Drudejevega klasičnega računa!
Dodatno branje lahko najdete v knjigah:
J.Strnad, FIZIKA, četrti del (učbenik za drugi letnik fakultete za fiziko)
Ashcroft, Mermin, SOLID STATE PHYSICS (“biblija” za učenje fizike trdne snovi)
