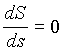| Slišal sem, da imamo lahko tekočo vodo tudi pri temperaturi pod lediščem vode (pri normalnem tlaku in navadni vodovodni vodi), vendar le, če gladina ostane mirna, oziroma ne premaknemo posode, v kateri je voda. |
Gre za pojav, ki ga fiziki imenujemo podhladitev oziroma pregretje. Če ga želimo razumeti, se moramo vsaj malo dotakniti Landau-ove teorije faznih prehodov. Navedimo najprej nekaj primerov faznih prehodov: zmrzovanje ali taljenje, izparevanje ali kondenzacija, prehod iz feromagnetika v paramagnetik, prehod iz neurejene v urejeno (na primer nematsko) fazo pri tekočih kristalih (v prvi fazi imamo opravka s popolno neurejenostjo smeri molekul – kot pri navadni tekočini, medtem ko v nematski fazi molekule kažejo pretežno v eno smer) Dogovoriti se moramo, kako sploh opišemo stopnjo urejenosti sistema, katerega fazni prehod opazujemo. V ta namen vpeljemo količino, ki ji pravimo parameter urejenosti, zanj pa velja, da je pod temperaturo faznega prehoda od nič različen, nad njo pa nič, tako da v bistvu meri urejenost nizkotemperaturne faze (nizkotemperaturna faza je vedno bolj urejena od visokotemperaturne, primerjaj led in vodo). V primeru prehoda med feromagnetikom in paramagnetikom kot parameter urejenosti služi spontana magnetizacija (namagnetenost). Globoko pod temperaturo prehoda doseže največjo možno vrednost, z višanjem temperature pa se manjša vse do vrednosti 0, ki jo ima v neurejeni paramagnetni fazi. Pri izparevanju za parameter urejenosti izberemo razliko med gostoto tekočine in gostoto plinaste faze pri vrelišču.
Fazni prehodi so lahko zvezni ali pa nezvezni. Pri drugih parameter urejenosti ob prehodu doživi nenaden skok, pri prvih pa se z njim ne zgodi nič dramatičnega, le počasi narašča, ko nižamo temperaturo. Prehod feromagnetik – paramagnetik je tipičen zvezni prehod, zmrzovanje in izparevanje tekočine ter prehod iz neurejene v nematsko fazo pa so nezvezni (zadnji je skoraj zvezen, kar pomeni, da parameter urejenosti ob prehodu le malo poskoči).
Preidimo k bistvu. Opis faznega prehoda si oglejmo za termodinamični sistem, katerega stanje opišemo s temperaturo T, tlakom p, prostornino V in parametrom urejenosti s. Vzemimo za začetek sistem s stalno prostornino in ga toplotno izolirajmo od okolice, tako da bo njegova notranja energija vseskozi enaka. Denimo, da parameter urejenosti sprva ne ustreza ravnovesnemu stanju, torej da je sistem bolj ali manj urejen kot v ravnovesju. Med približevanjem k ravnovesju bo naraščala entropija sistema, vse dokler ne bo dosegla maksimuma, pri tem pa se lahko spremenita tlak in temperatura. Sistem s konstantno energijo je v ravnovesju takrat, ko je njegova entropija maksimalna. Ker je v ravnovesju entropija sistema maksimalna, se skoraj ne bo spremenila, tudi če malce spremenimo parameter urejenosti (za ds). Če je ds resnično majhen, lahko to zapišemo z odvodom
.
Običajno pa pri faznem prehodu sistema ne izoliramo od okolice, niti ga ne držimo pri konstantni prostornini, ampak sta konstantna tlak in temperatura. Za tak primer je pripravno vpeljati novo količino, ki bo konstantna, kljub temu, da sistem od okolice prejema toploto (ker ni toplotno izoliran) in opravlja delo (ker volumen ni konstanten). To količino imenujemo prosta entalpija, definirana pa je z
,
kjer je Wn notranja energija, S pa entropija. Majhne spremembe proste entalpije dG se izražajo kot
.
Vidimo torej, da je prosta entalpija pri konstantnih tlaku in temperaturi ves čas enaka. To velja samo tedaj, če gre sistem le skozi ravnovesna stanja. Če pa se parameter urejenosti kot prej približuje ravnovesni vrednosti, se prosta entalpija manjša, vse do ravnovesja, kjer je minimalna. Ravnovesna vrednost parametra urejenosti je tista, pri kateri ima prosta energija minimum, kar zahteva
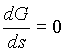
Vsa skrivnost torej tiči v odvisnosti proste entalpije od parametra urejenosti. Sedaj naredimo odločilni korak in zapišimo prosto entalpijo za majhne vrednosti parametra urejenosti, nekako takole:
Majhne vrednosti s so tudi tiste, ki nas zanimajo, saj opazujemo le okolico faznega prehoda (spomnimo se, da za visokotemperaturno fazo velja 
). Členi z višjimi potencami s so vse manjši in jih lahko spustimo. Linearni člen odpade, ker mora biti ravnovesna vrednost parametra urejenosti v visokotemperaturni fazi 0, kar zahteva, da pri velja 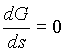. Pri prvem členu, ki ima ekstrem pri , si privoščimo preprosto odvisnost od temperature. S tem upoštevamo težnjo sistema po neurejenosti pri visokih temperaturah in po urejenosti pri nižjih. Pri visoki temperaturi T ima funkcija G(s) minimum pri s=0, to je torej ravnovesna vrednost parametra urejenosti.
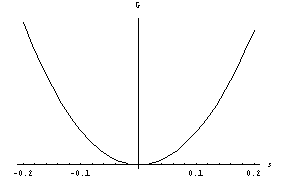
o sistem ohlajamo, pa se pojavi dodaten minimum pri s>0:
.
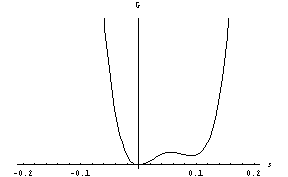Zdaj imamo dve ravnovesni stanji, stabilno, ki je globalni minimum proste entalpije, in metastabilno (nestabilno). Pri temperaturi faznega prehoda sta vrednosti proste entalpije v obeh minimumih enaki,
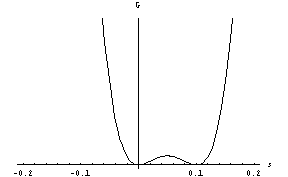
pod njo pa je G manjši v desnem minimumu, kar pomeni, da je zdaj stabilna ravnovesna vrednost parametra urejenosti od nič različna, pri s=0 pa imamo še vedno metastabilno ravnovesno stanje:
.
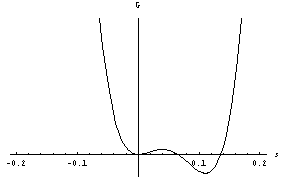Ko temperaturo znižamo do T*, prvi minimum dokončno izgine:
.
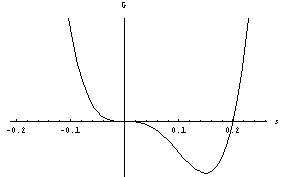Pravkar smo bili priča nezveznemu faznemu prehodu. Zanj je značilen obstoj dveh lokalnih minimumov proste entalpije. Če pa v razvoju G(s) manjka drugi člen (če je B=0), je situacija drugačna. To se zgodi pri sistemih, kjer -s predstavlja stanje z isto energijo kot s. Nad temperaturo prehoda imamo ravnovesje seveda spet pri s=0, kot prej. Pri temperaturi prehoda, ki je zdaj kar T*, obstaja še vedno le en sam minimum, a ni več tako oster:
.
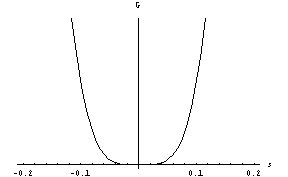Z nadaljnjim nižanjem temperature se minimum postopoma seli proti večjim vrednostim s (stanja z negativnimi s so pred prehodom fizikalno ekvivalentna tistim pri pozitivnih s, ob prehodu pa si sistem naključno izbere enega od obeh minimumov):
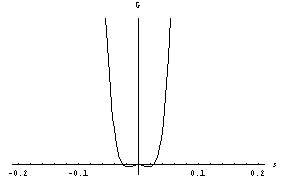
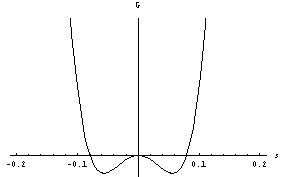
To je bil zvezni fazni prehod. Vrnimo se za hipec k nezveznemu, torej takemu, kjer je B različen od 0. Morda ste že sami ugotovili, da se odgovor na vprašanje o podhlajeni vodi skriva v obstoju metastabilnega ravnovesnega stanja, torej lokalnega minimuma proste entalpije, ki ni hkrati tudi globalni minimum. Vzemimo, da začnemo nad lediščem, kjer je stabilno tekoče agregatno stanje – sistem se nahaja v minimumu pri s=0 . Pri ohlajanju se pojavi nov lokalni minimum, kot smo videli prej, ki ustreza trdnemu agregatnemu stanju. Kljub temu, da se novi minimum nazadnje spusti pod prvega in postane stabilen, pa lahko sistem še vedno vztraja v prvem vse do temperature T*, ko ta še obstaja, če le motnje niso prevelike (mešanje tekočine in valovanje gladine sta zagotovo preveliki motnji). V domačem zmrzovalniku je to verjetno težko doseči, če ne zaradi drugega zato, ker se ne moremo izogniti nečistočam v vodi in vplivu stene posode. Oboje namreč vodnim molekulam vsiljuje neko ureditev, ki je nismo upoštevali; ta povzroči, da tekočina na teh mestih prej zmrzne, zmrzal pa se nato razširi naokoli. Na podoben pojav naletimo pri rasti kristalčkov na vrvici, ki jo pomolimo v prenasičeno raztopino, ali pa ob pogledu na kozarec piva, še posebej točenega, v katerem se dvigajo mehurčki CO2. Koncentracija CO2 v sveže natočenem pivu je večja od ravnovesne, zato se le-ta izloča, in to na nečistočah ob steni kozarca in v pivu. Bodite torej pozorni, močno izločanje mehurčkov ni razlog za veselje.
