Obroč okoli ekvatorja

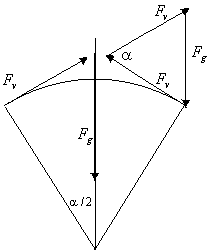
Seveda ne bi bilo nobenega problema, če bi naredili obroč s polmerom natanko enakim polmeru Zemlje. Tedaj bi se obroč tesno prilegal Zemlji, spodnji del obroča bi ležal na Zemlji ( v pravem fizikalnem duhu seveda zanemarimo gozdove, gore in podobne nepravilnosti, ki odstopajo od okrogle oblike). Silo teže na obroč bi tedaj uravnotežila sila podlage. Na ta način bi pravzaprav zgradili zid okoli ekvatorja. Povsem drugače pa je, če bi bil obroč nekoliko večji kot Zemlja. Kaj bi se zgodilo z obročem, ki bi bil na primer tako velik, da bi se vil nekaj kilometrov nad površjem Zemlje, pri čemer ga ne bi podprli z nikakršnimi stebri? Da bi lahko odgovorili na to vprašanje si oglejmo, kolikšna sila bi napenjala tanek obroč brez podpornih stebrov, ki bi ga sklenili okoli Zemlje. Sila v obroču mora v vsaki točki uravnovesiti silo teže (gravitacijski privlak Zemlje) na isti delček snovi. Proučimo torej ravnovesno stanje (glej sliko).

Delček na obroču preseka S in majhne ločne dolžine ima maso

kjer je R polmer kroga in gostota snovi, iz katere je obroč narejen. Sila v obroču zaradi sile teže je iz ravnovesnega pogoja

oziroma od tu napetost v obroču p (sila na presek obroča, pri računu uporabimo dejstvo, da je kot majhen, sinus kota pa tedaj kar enak kotu samemu)

Večji kot bo obroč, večja bo torej napetost v obroču. Ker poznamo polmer Zemlje (R = 6400 km), lahko sedaj ocenimo, kolikšna bi bila napetost v obroču, ki bi obdajal Zemljo. Če vzamemo za gostoto snovi, iz katere bi naredili obroč, (približno gostota betona), dobimo za napetost p = 3*10¹¹ N/m². Glede na to, da je meja trdnosti za večino snovi okoli 10⁸ – 10⁹ N/m², lahko zaključimo, da bi se obroč okoli Zemlje porušil (prelomil na najšibkejših mestih) pod lastno težo.

(Jure Zupan)

-