| Zanima me zakaj g znotraj Zemljinega površja narašča linearno? Kaj se tam dogaja s privlačnimi silami in z morebitnim medtlakom znotraj te Zemljine mase? |
Kot je ugotovil že Newton, je privlačna sila med dvema točkastima telesoma (z masama m in M) takole odvisna od njune medsebojne razdalje r:
kjer je G gravitacijska konstanta in znaša 6.67×10-11 Nm2kg-2. Isti izraz velja tudi za privlačno silo med točkastim telesom z maso m in razsežno kroglo z maso M, ko je točkasto telo zunaj krogle; r je v tem primeru razdalja med središčem krogle in točkastim telesom. Izraz pa je nekoliko drugačen znotraj krogle. Poglejmo si zakaj.
Predstavljajmo si votlo kroglo in nek predmet v njenem središču. Kolikšno privlačno silo čuti takšen predmet? Nobene! Če je predmet točno v središču krogle, ga na vse strani vleče enako močno, zato je vsota vseh sil enaka 0. Podobno pa velja tudi v primeru, ko telo ni točno v središču, ampak bliže površini, še vedno pa znotraj voltine. Sedaj je sicer razdalja do površine na eni strani nekoliko manjša, zato pa je privlačna sila večja. Na drugi strani pa je seveda nekoliko več snovi, zato je tudi na drugi strani sila nekoliko večja. Oba učinka se natanko izničita, zato kjerkoli znotraj votle krogle telo ne čuti gravitacijske privlačne sile take krogle. Sedaj ni več težko razumeti poteka gravitacijskega privlaka znotraj Zemlje.
Vzemimo, da želimo izračunati g na neki razdalji od središča Zemlje R. Zemljo razdelimo na dva dela: na manjšo kroglo s polmerom R in na votlo kroglo (votlina s polmerom R) Iz zgoraj povedanega sledi, da je celotna sila teže, ki jo povzroča votla krogla natanko 0; telo pod površino Zemlje čuti le privlak krogle s polmerom R. Ob predpostavki, da je gostota Zemlje povsod enaka (to je le predpostavka za preprost model – dejansko je napačna!) lahko zaključimo, da masa notranje krogle narašča kot R3, sila teže zunaj notranje krogle pa pada kot R2. Če združimo oba učinka, dobimo linearno naraščanje teže znotraj Zemlje.
Povzetek: pod površino Zemlje telo čuti le privlačno silo Zemlje “pod seboj” – privlačna sila lupine, ki je “nad njim” je natanko nič. Ker masa krogle “pod nogami” narašča kot R3, privlačna sila pa pada kot R2, znotraj Zemlje teža linearno narašča. Ko pa enkrat pridemo na površje Zemlje, s povečevanjem R masa nič več ne narašča, privlačna sila pa pada kot R2.
Kadar je sila teže neodvisna od globine, je pritisk sorazmeren z globino. Ker se znotraj Zemlje teža zmanjšuje, tudi pritisk ne narašča enakomerno z globino. Kratek račun (ob predpostavki, da je gostota Zemlje povsod enaka), da rezultat:
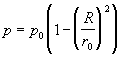
kjer je p0 pritisk v središču Zemlje, R razdalja od središča in r0 polmer Zemlje. Zanimivo je še pogledati, koliko je p0:
kjer je 
gostota Zemlje in g težni pospešek na površini Zemlje. Izraz močno spominja na znano formulo p =g h. Seveda, če namesto konstantnega g vzamemo njegovo povprečno vrednost (ker se spreminja linearno je njegova povprečna vrednost točno polovica vrednosti na površju), za globino pa polmer Zemlje, dobimo:
kar je pravilen rezultat. Kot že rečeno pa smo ob računu morali privzeti, da je gostota konstantna (kar je za resnično Zemljo napačno), linearni potek težnega pospeška je torej le grob približek resničnega spreminjanja v notranjosti Zemlje.
