Kako je definirana enota fon, ki naj bi merila jakost zvoka in kako se razlikuje od dB?
Obe enoti, fon in decibel, sta povezani z glasnostjo zvoka. Ločnica med njima pa je, kot bomo videli, kar nekoliko nejasna, še posebno pri uporabi v vsakdanjem življenju.
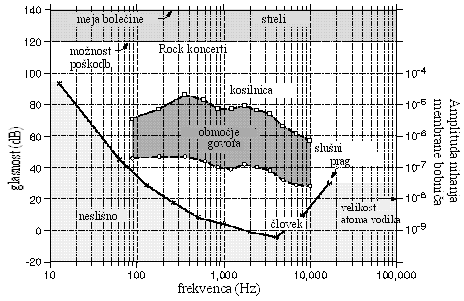
Da bomo lahko razumeli razliko, najprej uvedimo nekaj pojmov. Jakost zvoka je drugo ime za gostoto zvočnega energijskega toka. Jakost zvoka tako pove, kolikšen energijski tok na ploskovno enoto ima zvočni signal. Jakost oz. gostoto energijskega toka navadno označimo z malo črko j. Ko poslušamo glasbo, do nas prihaja zvok z različnimi frekvencami ν. Jakost zvoka je torej frekvenčno odvisna, j=j(ν). Zvok, ki ga lahko zazna človeško uho, ima frekvenco na območju 16 Hz do nekako 16 kHz – 20 kHz. Pri tem seveda človeško uho ni enako občutljivo za vse frekvence. Najbolj občutljivo je za zvok s frekvenco približno 2 kHz-3 kHz. Tedaj zazna človeško uho tudi še zvok z jakostjo nekaj manjšo od 10-12 W/m2. Za primerjavo: zvok z jakostjo 1 W/m2 povzroči občutek bolečine. Spodnja meja občutljivosti človeškega ušesa za zvok je, kot že rečeno, frekvenčno odvisna. To najnižjo mejo označimo z j0(ν) in je prikazana na Sliki 1.
Glasnost je količina, ki skuša povzeti občutek, ki ga v ušesu vzbudita tona z različnima frekvencama. Če imata tona z različnima frekvencama enako glasnost, vzbudita enak občutek v ušesu. Vendar, pozor, tona različnih frekvenc z enakima glasnostma imata lahko zelo različne jakosti! Huh, sliši se zapleteno, a sploh ni. Saj vendar vemo: za tone s frekvenco 3 kHz je človeško uho zelo občutljivo, medtem ko ni občutljivo za tone s frekvenco npr. 16 Hz. Da doseže enak občutek glasnosti v ušesu, mora torej ton s frekvenco 16 Hz nositi neprimerno večjo energijo kot tisti s frekvenco 3 kHz. Gornje razmišljanje lahko povzamemo z matematično formulo za glasnost zvoka z jakostjo j
glasnost=10 log(j(ν)/j0(ν)),
kjer je j0(ν) najmanjša jakost zvoka, ki jo še slišimo pri frekvenci ν (glej Sliko 1). Enota za glasnost je fon. Logaritem stoji v formuli, da opiše človekovo zaznavanje zvoka. Zvoka, ki ima stokrat večjo jakost (nosi stokrat večjo energijo), namreč ne slišimo stokrat glasneje, saj bi se nam vendar zmešalo. Veliko bolje naše občutke opiše logaritemska odvisnost, kot je zapisana zgoraj. Iz gornje definicije glasnosti tudi vidimo, da je glasnost količina, ki ima zapleteno frekvenčno odvisno zvezo z merljivimi količinami, to je z jakostjo zvoka. Zato je samo računanje glasnosti nekoliko nerodno. Mnogokrat tako v logaritem namesto frekvenčno odvisne najmanjše jakosti zvoka j0(ν), postavimo kar najmanjšo jakost j0 pri frekvenci 1kHz, ki je j0=j0(1kHz)=10-12W/m2. Količina 10 log(j(ν)/j0 ) ima enoto decibel (dB). Strogo gledano se tako fon in decibel ujemata le pri frekvenci 1kHz. A pogosto ljudje uporabljajo fon in decibel kot sinonima za eno in isto enoto. To je sicer nekoliko površno, a kljub vsemu ni povsem zgrešeno. V resničnem bivanjskem okolju namreč nimamo opraviti s čistimi zvoki, to je s toni ene frekvence, pač pa s šumi, to je z zvoki, ki vsebujejo zelo različne frekvence. Pri šumih je zato veliko težje določiti glasnost. Za vsakdanjo rabo lahko povzamemo približno glasnost različnih izvirov z naslednjo tabelo (ki je nenatančna tudi na deset fonov):
| Glasnost | Izvir zvoka |
| 0 fonov | zvok komaj slišimo |
| 10 | šelestenje listja v gozdu, šepet v razdalji 1m |
| 20 | tiktakanje ure v razdalji 1m |
| 30 | šum v gledališki dvorani |
| 40 | tiha glasba, radio v sobi |
| 60 | običajen govor v razdalji 1m |
| 70 | motor težjega avtomobila |
| 80 | šum na hrupni ulici |
| 90 | orkester v koncertni dvorani v skrajnem primeru |
| 100 | stroj za kovičenje |
| 110 | pnevmatično kladivo |
| 120 | reakcijski motor v razdalji 1m |
Če glasnost še naraste, se pojavi občutek bolečine in zvoka ne slišimo več.
Viri:
J. Strnad, Fizika, prvi del
Zapis na Wisconski Univerzi
Kako deluje sluh?
O razliki kvalitete zvoka na zgoščenki in na navadni vinilni plošči
(Jure Zupan)












