| Kaj bi se zgodilo, če bi se neko telo gibalo hitreje od svetlobe (npr. 600.000 km/s)? Ko se neko telo giblje hitreje kot zvok govorimo o prebijanju zvočnega zida. Ali bi v tem primeru lahko govorili o t.i. prebijanju svetlobnega zida? |
Kot je bilo že dostikrat omenjeno, se telesa, ki imajo od nič različno maso, ne morejo gibati s hitrostjo enako ali večjo od svetlobne hitrosti v vakuumu, ki je približno 300000 km/s. To je hkrati tudi odgovor na prvi del vprašanja.
Dostikrat pa smo tudi že omenili, da je hitrost svetlobe v snovi manjša od hitrosti svetlobe v vakuumu. To pomeni, da se v snovi telo lahko giblje hitreje kot svetloba (vendar še vedno ne hitreje kot svetloba v vakuumu)! V tem primeru zares pride do “prebijanja svetlobnega zida”. Prav tako kot ladja na morju za sabo pušča valovno čelo (val, ki se širi za ladjo in ima obliko črke V) in nadzvočno letalo za seboj vleče Machov stožec (to je valovno čelo, ki ga slišimo kot pok, ko nas preleti letalo z nadzvočno hitrostjo) tudi električno nabita telesa v snovi sevajo svetlobo Čerenkova, če so hitrejši od svetlobne hitrosti v tej snovi.
Pojav s pridom izkoriščajo v fiziki osnovnih delcev. Prav tako, kot v omenjenih primerih (ladja in letalo), je kot, pod katerim se širi valovno čelo, odvisen od hitrosti telesa. Večja je hitrost, večji je kot, pod katerim se širi valovno čelo. To pomeni, da iz meritve kota, pod katerim sevajo delci Čerenkovo svetlobo, lahko izračunamo s kakšno hitrostjo se gibajo. Za kot, pod katerim delci sevajo Čerenkove fotone () velja 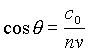
kjer je c0 hitrost svetlobe v vakuumu, n lomni količnik snovi in v hitrost delca. Vidimo, da telesa, ki se gibajo s hitrostjo manjšo od c0/n ne sevajo (kosinus nekega kota ne more biti večji od 1). Vzemimo, da imamo delca z eneko energijo (ki smo jo že izmerili), a imata različno maso. Zato se gibljeta z različno hitrostjo, ki pa jo lahko izračunamo iz kota, pod katerim izhajajo Čerenkovi fotoni. Iz znane energije in hitrosti pa lahko takoj izračunamo maso delca – delec smo identificirali. V primeru, ko je masa teles močno različna (hočemo ločevati med pozitroni in protoni), se lahko zgodi, da ima težki delec premajhno hitrost, da bi sploh lahko seval. V tem primeru je identifikacija še lažja – če delec seva (“prebije svetlobni zid”), je njegova masa majhna, če ne seva, je njegova masa velika. Drugi način za identifikacijo delcev je meritev gibalne količine in hitrosti. Iz teh dveh podatkov spet lahko izračunamo maso in tako ugotovimo, kateri delec je potoval skozi detektor.









