Domov Tolmačenje znanosti Filozofija in zgodovina Zlati rez

Zlati rez

Piše:

25. 3. 2003

Pred nekaj leti sem se trudil, da bi narisal čim boljši akt. V knjigah sem zasledil trditev, da je očesu najbolj prijetna kompozicija v zlatem rezu. Zlati rez naj bi bil najboljše možno vodilo vseh, ki poskušajo skladno lepoto ujeti v sliki. Pred kratkim pa mi je prijatelj fizik, med počitkom na krajšem kolesarskem izletu, pokazal bližnjo sončnico in začel govoriti o številu krivulj, ki jih tvori razporeditev semen na cvetu. Razlagal je tudi o Fibonaccijevih številih in o zlatemu rezu. Tako sem se spet srečal z razmerjem zlatega reza, ki me je tokrat presenetil na področju, kjer ga nisem pričakoval – v matematiki in biologiji.

Fibonaccijevo zaporedje in razmnoževanje zajcev

Srednjeveški matematik Fibonacci, ki je živel v dvanajstem stoletju našega štetja, je znan predvsem po tem, da je v Evropo vpeljal indo-arabski številski zapis, ki je bistveno olajšal računske operacije. Ker je bil novi zapis praktičen, so ga hitro sprejeli v trgovskih krogih, ki so prav takrat ponovno doživljali razcvet. Med problemi s katerimi se je ukvarjal Fibonacci, je bila tudi zanimiva vrsta števil, ki jo danes imenujemo »Fibonaccijevo zaporedje«.

Nekoč ga je zanimalo, kako hitro bi se lahko v idealnih okoliščinah razmnoževali zajci. Recimo, da imamo en par zajcev (samca in samico), ki bi se jima, vsak mesec rodil nov par zajcev (eden ženskega in eden moškega spola). Čas, potreben za dosego reproduktivne sposobnosti je pri zajcih dolg en mesec. Predpostavimo, da naši zajci nikoli ne umrejo, samica pa, kot že rečeno, od drugega meseca naprej rodi vsak mesec nov par.

Po prvem mesecu se prvi par že pari, vendar je v kletki še vedno le en par.
Na koncu drugega meseca samica povrže nov par zajcev, tako da sta sedaj v kletki 2 para.
Ob koncu tretjega meseca prvotna samica da svoj drugi par, druga samica pa še ni spolno zrela. V kletki so 3 pari zajcev.
Po štirih mesecih dve samice, prva in druga povržeta nova para, tako, da je sedaj zajcev 5.

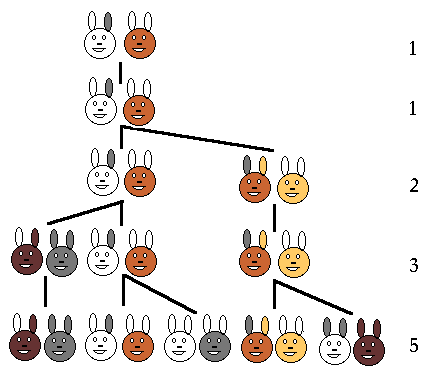
Število parov narašča v naslednjem zaporedju: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55… Števila, ki jih tako dobimo, tvorijo tako imenovano Fibonaccijevo zaporedje, ki ga lahko povzamemo z naslednjo formulo:

F(n) = F(n-1) + F(n-2)

Seveda je zgoraj opisani miselni eksperiment dokaj neživljenjski, vendar nam njegova rešitev da zaporedje, ki je presenetljivo povezano z razmerjem zlatega reza, s številom Φ = 1,618034. Če pogledamo razmerje med sosednjimi členi zaporedja (delimo naslednjega s prejšnjim) vidimo, da dobimo naslednja števila:

1/1=1; 2/1=2; 3/2=1,5; 5/3=1,666…; 8/5=1,6; 13/8=1,625; 21/13=1,61538…

Ko napredujemo po zaporedju, opazimo, da razmerje konvergira proti določeni vrednosti, ki ji pravimo zlato razmerje: približno 1,618034… Temu številu pravimo tudi zlati rez, zlato število, ki je predstavljeno z veliko grško črko Φ je neposredno povezano z malim zlatim rezom mali φ, ki je le del velikega za decimalno vejico.

Števili A in B sta torej v zlatem rezu, če zanju velja enačba: A / B = B / (A+B).

Fibonaccijeva števila v naravi

Zanimivo je, da najdemo v naravi Fibonaccijeva števila na mnogo krajih. Pri nekaterih rastlinah se Fibonaccijeva števila pojavljajo, ko štejemo, kako so listi razporejeni okoli stebla. Če pogledamo na rastlino od zgoraj, so listi večinoma razporejeni tako, da prestrežejo največjo možno količino sončni žarkov, se pravi, da zgornji listi ne prekrivajo spodnjih.

Pri teh rastlinah na Fibonaccijeva števila naletimo:
– ko štejemo razporeditev cvetnih listov v cvetu,
– v številu krogov, ki jih v smeri urinega kazalca naredimo, ko štejemo koliko listov je med spodnjim in prvim, ki ga prekriva,
– v razporeditvi semen v cvetu in storžih

Na sliki vidimo, da rumeni listki tvorijo spirale, ki so usmerjene v dve smeri, levo in desno. Če na robu cveta preštejemo spirale, ki so ukrivljene v desno, ko se premikamo proti robu cveta vidimo, da jih je 55. Malo bližje centru jih je 34. Števili spiral usmerjenih v levo in tistih, ki so usmerjene v desno, sta sosednji Fibonnacijevi števili. Isto se zgodi v veliko cvetovih. Zakaj?

Odgovor je verjetno v enem osnovnih načel narave – njeni ekonomičnosti. Rastlina ima največ možnosti za preživetje, če se lahko uspešno postavi po robu vsem dejavnikom, ki vplivajo na njen razvoj. To pomeni, da morajo biti izkoristki naravnih virov, ki so potrebni za njeno rast in odpornost na zunanje dejavnike (veter, gravitacija…) optimalni.

Kakšna je povezava med zlatim rezom in rastlinami, pri katerih se pojavlja?

Odgovor se skriva v učinkovitosti porabe prostora. Kvadratne kocke zavzamejo najmanj odvečnega prostora, če so zložene v kvadratni škatli dimenzije, ki se ujema z večkratnikom njihovih stranic. Okrogli predmeti bolje zapolnijo heksagonalno strukturo. Semena so večinoma okrogla, vendar pa niso razporejena v heksagonalni strukturi. Čeprav je heksagonalna simetrija najboljša oblika pakiranja za okrogla semena, pa ne ustreza razporeditvi listov okoli stebla in pakiranju okroglih cvetov s semeni, ki rastejo.

Botaniki so odkrili, da rastline rastejo iz male skupine celic (meristema), ki ga najdemo na vrhu vsakega stebla in poganjka iz njega. Le tu nastajajo nove celice, ki se razporejajo v spirali okoli meristema. Kasneje te nove celice le rastejo (nimajo sposobnosti delitve).

Zanimivo je, da je le en kot med novimi celicami, ki rast ureja tako, da bi rastlina dosegla optimalno formo, v kateri bi se kar najmanj listov prekrivalo, ne glede na velikost rastline. Podobno nova semena izpodrinejo stara, ki se premaknejo proti robu cveta ohranijo pa svoj kot, za katerega izgleda, da vlada rastlini ne glede na to, kako velika zraste. Kot kaže uporablja narava isti vzorec pri pakiranju semen v cvet, kot ga je uporabljala pri razporejanju cvetnih listov okoli cveta in listov okoli stebla. Poleg tega ostane vzorec navzoč tudi pri kasnejši rasti rastline. Kot v katerem se vrstijo nove celice okoli meristema je φ obrata za novo celico.

Če so listi na rastlini razporejeni po principu Φ (1,618…) listov na obrat okoli stebla (ob rasti okoli meristema), bo vsak list na rastlini dobil maksimalno količino svetlobe, s tem, da bo metal najmanj sence na druge. Tako bo ujel tudi največ dežnih kapelj, cvet pa bo najbolj izpostavljen insektom potrebnim za oploditev. Cela rastlina, njeni listi, cvetni listi in semena so postavljeni po razmerju zlatega števila in njegovim približkom iz celih števil (Fibonnacijeva števila).

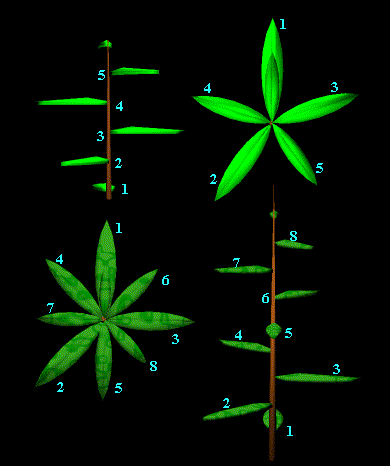
Zakaj je zlati rez najboljše število za optimalno pakiranje?

Kaj bi se zgodilo, če bi rasti novih celic okoli meristema vladalo neko drugo razmerje – recimo 0,5 ali 0,6 ali 0,48?

Če bi nastajale v razmerju 0,5 obrata za seme, bi dobili strukturo cveta z dvema poganjkoma, ki bi bila zelo neučinkovita – veter bi jo lažje podrl. Okrogel cvet je bolj kompakten in ima večjo moč upiranja dežju in vetru.

Če novo seme nastane po 0,48 obrata dobimo dve spiralasti roki, ki imata malo manj kot 0,5 obrata razmaka.

Če je med sosednjima semenoma 0,6 obrat dobimo strukturo s petimi rokami. Ker je 0,6 = 3/5, bodo trije obrati proizvedli 5 semen, s tem, da bo 6. seme na isti roki, kot prvo, sedmo v isti poziciji kot drugo itd.

Za nas je pomembna informacija le decimalni del števila, saj nam prvi pove le koliko obratov je bilo narejenih, decimalni pa govori o kotu znotraj enega obrata. Ko se velikost kota bliža φ (0,618033) postaja izkoristek prostora boljši, vendar pa so pri vrednosti 0,61 še vedno opazne praznine blizu centra. Vidimo, da vsako število, ki se ga da zapisati kot zaključeni ulomek (racionalno število) onemogoča optimalni izkoristek prostora, saj se koti začnejo ponavljati, vmes pa nastane praznina. Dobro število bi torej moralo imeti decimalni del, ki se nebi začel ponavljati. Ta števila imenujemo iracionalna, med katere spadajo npr. $\sqrt{2}$ , Φ, φ, e (Eulerjevo število = 2,71828..), $\pi$ (3,14159..) in njihovi večkratniki.

Razporeditvi semen s kotoma e in $\pi$ kmalu začneta proizvajati prazne prostore. Prva ima sedem »rok« saj je med semeni 0,7182.. obrata, kar je malo več kot 5/7 (=0,71428..). $\pi$ razporeditev je blizu 1/7=0,142857, kar da spiralasto razporeditev rok, podobno kot e.

In katero je najboljše iracionalno število za pakiranje? Tisto, ki se ne zaustavi za dolgo na racionalnem približku. Matematiki jim pravijo ugnezdeni ulomki. Najpreprostejši primer ugnezdenega ulomka je :

1/(1+1/(1+1/(1+1/(1+1/(1+/….)))) = φ

Njegovo vrednost lahko izračunamo, če ga prevedemo na kvadratno enačbo φ = 1/(1+φ).

\phi=\Phi-1=(\sqrt{5}-1)/2

Skrivnostno ujemanje kulture in nature v zlatem rezu

Vprašanje, ki se odpira ob tej nenavadni korespondenci lepote, narave in matematike, je dokaj nenavadno. Kako to, da razmerje, ki se tako pogosto pojavi v naravi in odraža njeno ekonomičnost in učinkovitost, vlada tudi svetu lepote in kulture, ki ga nekaj tisočletij gradimo vzporedno naravi? Je zlati rez res prijeten našim očem zgolj zato, ker smo nanj navajeni, ker ga opažamo v naravi?

Glej tudi: