In vendar se vrti: krilo

Če hočemo govoriti o krilu, se je najprej smiselno vprašati, kaj krilo sploh je? Seveda najprej odpremo leksikon, v katerem je krilo med drugim definirano za nosilno konstrukcijo pri letalu. Ker ta razlaga naši radovednosti ne zadosti, si z razmislekom pomagajmo sami. Naj bo krilo vsak predmet, ki je v toku tekočine zmožen ustvariti silo dviga.

Krilo v idealni tekočini

Seveda je vseeno, ali se krilo giblje v mirujoči tekočini, ali pa miruje v toku tekočine. Zato bomo govorili o relativni hitrosti krila glede na tekočino. V nadaljevanju se bomo omejili na gibanje v idealni tekočini. To bolj učeno povedano pomeni, da bomo zanemarili viskoznost in stisljivost tekočine, hkrati pa bomo krila opazovali v laminarnem toku tekočine. Takoj se moramo vprašati, ali je takšna obravnava realno sploh smiselna?

Ker bomo obravnavali relativno gibanje krila v zraku, ki je mešanica plinov, smo takoj zadostili pogoju neviskoznosti. Ta je za zrak stokrat manjša kot za vodo in desettisočkrat manjša kot viskoznost lahkega strojnega olja. Za boljšo predstavo vzemite tri kozarce in enega napolnite z oljem, drugega pa z vodo. Ko boste z žlico hoteli mešati vsako izmed vsebin posameznega kozarca posebej, boste z lahkoto opazili, da najmanj moči porabite za mešanje zraka. Glede na vodo in olje lahko dobite celo varljiv občutek, da zrak žlice sploh ne zavira.

Druga nadloga je stisljivost, za katero pa se izkaže, da je pri hitrostih, s katerimi se bomo ukvarjali (0m/s do 130m/s), bolj ali manj konstantna. Nezanemarljive spremembe stisljivosti se pojavijo, ko je hitrost krila v zraku primerljiva s hitrostjo zvoka (331m/s pri 0°C). S tem, ko smo izbrali glede na zvok sorazmerno majhne hitrosti, smo se rešili tudi problema turbulenc, če le ne bomo krila v tekočini preveč nagibali.

Težave nam utegne povzročati še gibanje zraka vzdolž krila. V obravnavi bomo privzeli, da le-tega ni, saj bomo obravnavali modele kril s konstantnim presekom po dolžini.

Delovanje krila

Z eksperimentiranjem v vetrovniku, lahko pa tudi z opazovanjem gibanja bolj viskozne tekočine okoli modela krila, hitro opazimo, da ima tekočina na zgornji strani krila večjo hitrost kot na spodnji strani. Še več; opazimo lahko, da delca tekočine, ki sta bila pred krilom drug ob drugem, za krilom nista več skupaj, če je en potoval po zgornji, drug pa po spodnji strani.

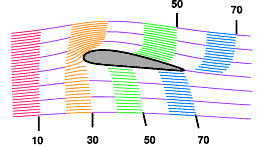Slika 1: Profil krila v toku tekočine. Opazen je zaostanek tekočine pod krilom.

Razloga za spremembo hitrosti pa ne smemo videti v razliki med dolžinama zgornjega in spodnjega dela krila, temveč v medsebojni povezanosti delcev tekočine. Delec ob krilu lahko nekako sporoči delcu, ki je od krila še nekoliko oddaljen, da se v tekočini nahaja ovira. S tem pa bo povzročil spremembo gibanja tekočine pred krilom. Pot, ki bi jo delec opisal pri neoviranem gibanju, torej ne more biti enaka poti gibanja delca, ko njegovo gibanje zmoti ovira. V obeh primerih imenujmo takšno pot tokovnica (vijolična črta na sliki 1). Opisano delovanje enega dela tekočine na drugi del povzroči na nekem mestu zgostitev, na drugem pa razredčitev tokovnic. Opazimo še, da je hitrost tekočine v območju zgostitve tokovnic večja, kot v območju razredčitve.

Zaradi ohranitve energije pri gibanju smemo opisne spremenljivke tekočine povezati z Bernoullijevo enačbo. Ker nas bosta zanimala le hitrostni in tlačni del, jo lahko zapišemo kot:

Torej je tlak na področju višjih hitrosti nižji, kot na področju nižjih hitrosti. Ker je tako tlak pod krilom višji kot nad krilom, začne na krilo delovati sila dviga v smeri navzgor.

Opis krila s pomočjo cirkulacije

Dogajanje ob krilu si lahko predstavimo tudi drugače. Zamislimo si zanko, ki je zaključena sama vase in objema krilo (slika 2). Oblika zanke ni pomembna. Iz zgoraj navedenih razlogov je razvidno, da se velikost hitrosti in njena smer vzdolž zanke spreminjata. Zanko razdelimo na veliko zelo majhnih delov dolžine dz in za vsak del posebej ugotovimo, kakšni sta na njegovi sredini velikost in usmerjenost hitrosti. Vsoti skalarnih produktov vektorjev odsekov ter vektorjev hitrosti rečemo cirkulacija. Zakaj?

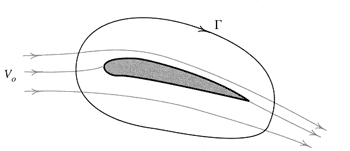Slika 2: Definicija cirkulacije.

Večina nas ob tem pojmu takoj pomisli na vrtenje, vendar ga tukaj ni. Vsaj na prvi pogled ne. Na zgornjem odseku krivulje imata hitrost in odsek enako usmerjenost horizontalne komponente, medtem, ko se smeri na spodnjem delu razlikujeta. Pri računanju skalarnega produkta bodo takšni deli dobili negativen predznak, in se bodo od vsote odšteli. Vemo, da so hitrosti pod krilom manjše od hitrosti nad krilom. Torej si lahko mislimo, da smo spodaj konstantni hitrosti odšteli zgoraj pa prišteli en del hitrosti. Del, ki smo ga zgoraj prišteli mora imeti horizontalni del istosmeren kot vektor konstantne hitrosti, na spodnjem delu pa je ta vektor nasprotno usmerjen. Cirkulacijo si tako lahko predstavljamo kot neke vrste vrtenje vektorja hitrosti (slika 3).

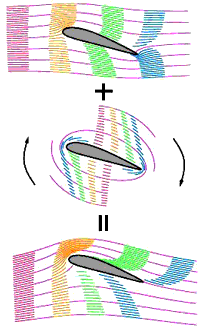Slika 3: Polju, ki sile dviga ne zagotavlja (G=0) prištejemo polje tekočine, ki je samo krožno (ni odtoka in pritoka) , pri čemer dobimo sliko, ki jo poda sam eksperiment.

Z nekaj matematičnega znanja lahko na podlagi teh ugotovitev izrazimo vertikalno in horizontalno komponento sile, s katero tekočina deluje na krilo. Teoretično se izkaže, da tekočina deluje na krilo le v vertikalni smeri, kar pomeni, da upora praktično ni (seveda, saj smo zanemarili viskoznost). Vertikalna komponenta se izraža kot produkt velikosti hitrosti, ki jo ima tekočina daleč proč od krila v₀, cirkulacije G, razpona krila l ter gostote tekočine , v kateri se krilo nahaja, in je usmerjena navzgor, ko je cirkulacija pozitivna (smer urinih kazalcev). Sklopu enačb, ki opisujeta velikost komponent sile tekočine na krilo, rečemo teorem Kutta-Joukowsky:

Vrteča se krila

Za silo dviga je torej ključnega pomena, da krilo ustvari pozitivno cirkulacijo. Krila, ki jih srečujemo najbolj pogosto, jo ustvarjajo zaradi svojega prečnega preseka ter nagnjenosti glede na smer hitrosti tekočine daleč pred krilom. Zanima nas, ali lahko temu pogoju zadostimo še kako drugače. Zadeva je zelo preprosta. Zakaj ne bi poskusili vrteti kar krila samega? Takoj nam lahko postane jasno, da s profili kril, ki so trenutno v uporabi, pri tej razpravi ne bomo prišli daleč, zato si raje oglejmo kak bolj preprost zgled.

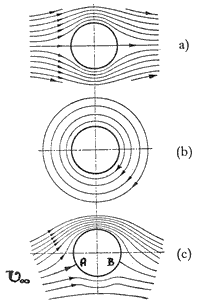Slika 4: Ekvivalent sliki 3, le da sedaj sami ustvarimo cirkulacijo z vrtenjem valja

Predstavljajmo si valj, ki se okoli svoje osi vrti v toku tekočine. Dokler vrtenja ni, je slika tokovnic pod in nad valjem simetrična (slika 4a). Takoj, ko dodamo temu polju še polje, ki ga ustvari valj z vrenjem (4b), postane slika tokovnic močno asimetrična (4c). Na zgornjem delu valja se tokovnice zgostijo, na spodnjem pa razredčijo. Opazimo lahko tudi dve točki, v katerih se tokovnica sreča z valjem. V takšni točki je velikost hitrosti tekočine enaka nič, zato ji rečemo stacionarna (če pogledamo sliko hitrostnega polja tekočine ob krilu, bomo takšne točke zasledili tudi ob njem). Morda je smiselno omeniti tudi, da je število takšnih točk močno odvisno od hitrosti vrtenja valja, hkrati pa tudi od hitrosti tekočine. Pri visokih vrtljajih takšne točke sploh ni, pri visokih hitrostih, ko pride do turbulentnega gibanja za valjem, pa so lahko take točke tudi tri.

Čeprav je primer enostaven, odpira kar nekaj vprašanj. Na začetku članka smo predpostavili, da je tekočina neviskozna. Če bi bilo to res, bi lahko vrteli naš valj s poljubno kotno hitrostjo in to ne bi vplivalo na tekočino. Površina valja namreč interagira s tekočino ravno zaradi viskoznega trenja, zato se moramo viskoznosti zavedati, čeprav jo v izračunih in dobljenih rezultatih zanemarjamo.

Vprašljiva postane tudi neposredna uporaba Bernoullijeve enačbe. Energija sistema namreč ni več konstantna, saj z vrtenjem valja vedno znova vlagamo vanj nekaj dela. Vendar je hitrost tekočine nad valjem v primeru njegovega pozitivnega vrtenja vedno večja, kot je pod njem, zato lahko na podlagi slike tokovnic sklepamo, da bo vertikalna komponenta sile usmerjena navzgor.

Teoretični izračuni ta rezultat potrdijo; še več, rezultat je enak teoremu Kutta-Joukowsky. Torej tudi teorija potrjuje, da je vrtenje valja v gibajoči se tekočini ekvivalentno klasičnemu krilu. Zmožnosti ustvarjanja sile, ki deluje pravokotno glede na smer gibanja telesa, z opravljanjem mehanskega dela (vrtenje), rečemo Magnusov efekt (glej tudi članek Nogometna fizika).

Jadrnica na Flettnerjeva jadra

Prva praktična uporaba vrtečega se krila pa ni bilo letenje, ampak plovba po vodah. Ob koncu dvajsetih let dvajsetega stoletja je Nemec Flettner zgradil jadrnico, ki je namesto standardnega jadra uporabljala dva pokončna valja višine 18 metrov, ki sta se vrtela okoli navpične osi. Ko je ladja plula z bočnim vetrom, sta vrteča valja ustvarjala silo, ki je ladjo pospeševala pravokotno glede na smer vetra. S tako opremljeno ladjo je bilo mogoče jadrati do 20° proti smeri vetra. Prednosti takšnih jader so se pokazale v možnosti regulacije hitrosti ladje s spreminjanjem kotne hitrosti vrtenja cilindrov, hkrati pa je tako vrtenje kot tudi oblika valjev zagotavljala boljšo stabilnost ladje. Ob močnih sunkih vetra je namreč upor klasičnih jader velik in povzroči bočno nagibanje ladje, pri valju pa so ti efekti bistveno manjši.

Ko valjasta jadra zares delujejo, se v začne zrak spiralasto ovijati okoli valjastih jader, kar poruši eno izmed naših začetnih predpostavk, hkrati pa se izraža tudi v povečanju upora valjev. To dogajanje do neke mere ublažimo tako, da valju dodamo diske, ki ga razdelijo na več delov, ali pa enostavno onemogočajo pretakanje zraka mimo stranskih robov (slika 5).

Slika 5: Ladja Bruckau.

Ladja, opremljena s tako imenovanimi Flettnerjevimi jadri, je bila zmožna tudi vzvratne plovbe in zelo učinkovitega zaviranja. To so mornarji dosegli z enostavno spremembo smeri cirkulacije (valja so začeli vrteti v nasprotni smeri kot prej). Prav tako pa so lahko pluli že ob zelo šibkih vetrovih, če sta se le valja vrtela dovolj hitro. Sicer je res, da ladja v brezvetrju valjev ni mogla uporabiti, je pa lahko preusmerila delo, ki so ga sicer opravljali stroji za vrtenje valjev, na pogon elis, in si tako plula tudi v brezvetrju.

Ob vsem tem čislanju se pojavi vprašanje, zakaj takšnih ladij danes ne vidimo prav pogosto. Razlog se bolj ali manj skriva v nizki ceni nafte, saj je ladja na motorni pogon v trgovskem smislu bolj zanesljiva, kot jadrnica. Če se to komu ne zdi zadosten razlog, pa naj si poskuša predstavljati velikost in količino jader, ki bi jih morali namestiti na  kakšen tanker.

Mlin na veter

Jadra tega tipa niso ostala le na vodi, temveč so jih hitro uporabili tudi pri izdelavi mlinov na veter (slika 6).

Slika 6: Mlin na veter.

Ponovno sta vodilna razloga za uporabo vrtečih valjev boljša kontrola delovnih pogojev in večji izkoristek, saj takšen mlin ob resonančnih sunkih vetra ni mogel ponoreti, kar se je dogajalo pri mlinih, ki so uporabljali lopute. Vendar so kmalu ugotovili, da je postopek predrag, saj bi morali vsako izmed jader razdeliti na več delov, ker se mora posamezno jadro ob osi vetrnice vrteti z manjšo hitrostjo, kot daleč proč od osi, to pa pomeni, da moramo valju vzdolž njegove dolžine spreminjati kotno hitrost. Poleg tega moramo dovajati še delo za vrtenje samih valjev. Realizacija z dobrim izkoristkom tako postane prezahtevna in predraga. Morda pa bi le lahko naše jadro prepričali, da bi se vrtelo samo od sebe? Zakaj bi uporabljali motorje za vrtenje kril, če lahko vrtenje zagotovi že sam tok tekočine? To nas pripelje do pojma avtorotacijskih teles.

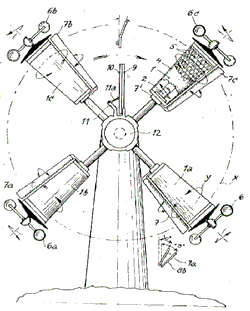Skica avtorotacijskega mlina.

Cilj je povečati izkoristek krila. Tok tekočine naj torej krilo vrti, hkrati pa zaradi vrtenja krilo v istem toku tekočine ustvari Magnusov efekt. Poskus, da bi se valj sam od sebe zavrtel v enakomernem toku, bo zelo hitro propadel, zato moramo poiskati obliko krila, ki bo za ta namen bolj pripravna.

Tokatyjevo krilo

Zamislimo (in izvedimo) si naslednji eksperiment: list papirja okvirnih dimenzij 5cm * 15cm držimo v zraku (majhna viskoznost) meter in pol nad podlago. Najprej ga obrnimo tako, da bo njegova površina vzporedna s tlemi. Ko ga spustimo, bo list med rahlim zibanjem padal skoraj navpično navzdol. Če pa poskus ponovimo tako, da papir pred spustom obrnemo tako, da je kot med njegovo površino in tlemi pravi, pa se bo začel papir vrteti okoli daljše osi. Opazili bomo, da papir ne leti več navpično navzdol, temveč se od prvotne navpičnice naglo oddaljuje. Zakaj?

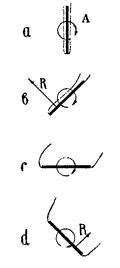Slika 7: Maxwellov eksperiment.

Papir zaradi spremenljivega upora pada hitreje (slika 7) iz lege a v lego b, kot iz lege c v lego d. Pri rezultanti sil takšnega gibanja se zato pojavi komponenta, pravokotna na smer padanja. Ta poskus je nadaljeval Riabouchinsky, ki je ugotovil, da je obtekanje robov listka bistveno za večji izkoristek. V primeru b hočemo tokovnice čim bolj zgostiti (gladko obtekanje), v položaju d pa naj bodo tokovnice čim bolj vsaka k sebi (negladko obtekanje).

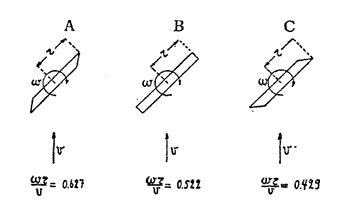Slika 8: Ryabouchinskyjev eksperiment. Odvisnost hitrosti vrtenja listka in hitrosti padanja pri različnih robovih.

Kot je razvidno s slike 8, da največje razmerje ploščica A, o čemer se lahko hitro sami prepričamo s skiciranjem tokovnic pri posameznih položajih krila. Izkoristek lahko povečamo tudi tako, da ploščico po vsej dolžini zvijemo v obliko črke S. Izkoristek se je s tem povečal, vendar smo z novo obliko definirali smer, v katero se bo ploščica zavrtela. Da bi zagotovili čim lepše obtekanje tokovnic mimo krila, zamaknimo obe polovici črke S proti osi, kot kaže slika 9.

Slika 9: Krilo v obliki zamaknjene črke S.

Vendar tudi s takšno rešitvijo še nismo popolnoma zadovoljni. Že res, da je krilo zelo učinkovito ustvarja rotacijo, vendar pa to ne velja tudi za dober izkoristek pri sili dviga, če ga primerjamo z valjem. Zato ustvarimo kombinacijo obeh, ki ji rečemo Tokatyjevo krilo (slika 10). Le-to ima za osnovo valj, ki ima na obeh straneh pritrjeni krili z obliko zamaknjene črke S.

Slika 10: Tokatyjevo krilo.

Letala s takšnimi krili obstajajo zaenkrat le v obliki sofisticiranih otroških zmajev, saj bi pri zahtevnem letenju povzročala preveč težav. Kot vemo je sila dviga odvisna od cirkulacije, torej od hitrosti vrtenja krila, ta pa je v našem primeru odvisna od hitrosti, s katero se letalo giblje skozi tekočino. Če bi se hitrost vrtenja naenkrat zmanjšala, bi se drastično zmanjšala tudi sila dviga, s čemer pa se noče soočiti noben resen pilot. Prav tako si težko predstavljam nadzvočna letala s takšnimi krili, kar pa v današnjem svetu, ko je za večino ljudi hitrost transporta pomembnejša od njegove cene, pomeni, da razvoj takšnih letal ekonomsko zaenkrat ni smiseln.

Nekaj delujočih aplikacij

Uporaba Magnusovega efekta je dandanes že dokaj popularna. Na ladjah Jacquesa Cousteauja lahko tako opazimo visoke cilindre, ki potisno silo ustvarjajo na malce drugačen način kot Flettnerjevi rotorji. Cilinder ima namreč na bočnih straneh po dolžini luknje, skozi katere motor srka zrak. Zaradi tega se na isti strani pred luknjo pojavi zmanjšan zračni tlak, ki zagotavlja potisno silo (slika 11). Ladja je tako ekološko bolj sprejemljiva kot izključno motorna plovila.

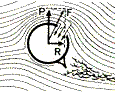Slika 11: Princip delovanja Cousteaujevega Turbosaila.

Slika 12: Cousteaujeva ladja Alcyone.

Podoben sistem uporabljajo tudi kot nadomestek repnega rotorja pri helikopterjih. Skozi ozko režo vzdolž ene strani repa piha zrak, ki vpliva na tok zraka, ki ga ustvarja glavni rotor. Na eni strani repa se zato pojavi nadtlak, ki helikopterju omogoča stabilizacijo (slika 13). S tem sistemom so zmanjšali število nesreč, ki so se zgodile na zadnjem delu helikopterja za 75%.

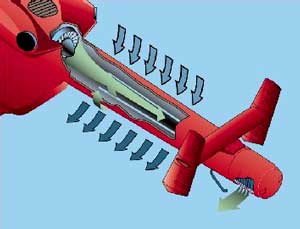Slika 13: Nadomestek za repni rotor na helikopterju.

Literatura

• G.A.Tokaty: A History and Philosophy of Fluid Mechanics, Dover Publications, Inc., New York, 1994.
• Street, Watters, Vennard: Elementary Fluid Mechanics, John Wiley & Sons, Inc., New York, 1996.
• John S. Denker: See How It Flies
• Cousteau Society
• Rotorcraft helicopters

Luka Vidic, kvarkadabra.net – številka 11 (oktober 2001)

-