Vzhajanje in zahajanje Sonca

Odgovor se skriva v nagnjeni rotacijski osi Zemlje, ki znaša (kot med ekliptiko in ravnino ekvatorja).

Najprej pozabimo na vrtenje Zemlje okoli lastne osi in opazujmo le kroženje okoli Sonca (za kar predpostavimo sprva kar pravilno krožnico). Ko Zemlja kroži okoli Sonca, je v vsakem trenutku polovica sfere osvetljena (na zemlji je dan), druga polovica pa v senci (noč). Ko naredi Zemlja v enem letu celotno pot okoli Sonca, naredi tudi ravnina, ki je meja med nočjo in dnevom, poln obrat. Preselimo se sedaj na Zemljo, ki naj se še vedno ne vrti. Meja med nočjo in dnevom glede na nas vrti, tako da v enem letu naredi poln obrat.

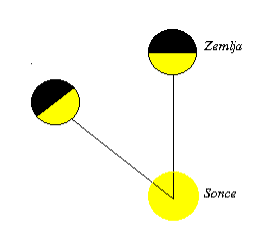
Sedaj vključimo v razpravo še lastno vrtenje Zemlje. Ko bomo imeli enakonočje, bo mejna ravnina obrnjena tako, da bo vsebovala tako os vrtenja Zemlje okoli svoje osi kot pravokotnico na ekliptiko (na Sliki 2 bi torej bila meja med dnevom in nočjo kar ravnina slike). Ob solsticiju pa bo mejna ravnina pravokotna na sliko (polovica Zemlje na Sliki 2 bi bila svetla, druga temna, glej tudi sliko 3.). Na sliki je nakazana naša geografska širina (črtkana črta). Medtem ko se zemlja vrti, naša lega kroži po krožnici (enaka vzporedniku).

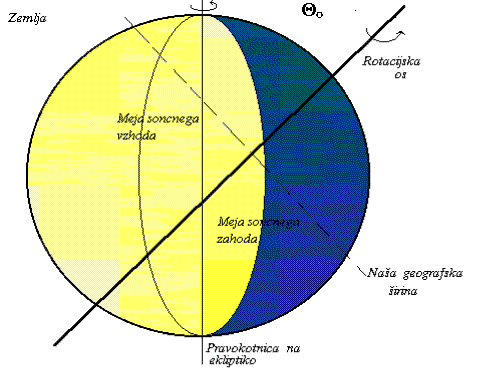
Ker je os vrtenja nagnjena, sta noč in dan različno dolga, pač odvisno od tega, kako je usmerjena mejna ravnina. Ob enakonočju (tako pomladnem, kot jesenskem) sta noč in dan enako dolga, kot pove že samo ime. Ob zimskem solsticiju je dan krajši kot noč, saj smo ob enakomernem kroženju manj časa osvetljeni, kot smo v senci (Slika 3, osvetljeni del črtkane črte je daljši kot temni del). Ravno nasprotna situacija (zamenjata se temni in svetli del), je pri poletnem solsticiju.

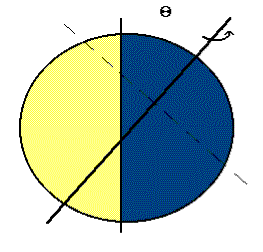
Sedaj pa k odgovoru na zastavljeno vprašanje. Sonce vzide, tedaj ko pri vrtenju prestopimo mejno ravnino iz teme na svetlo (na Sliki 2 v ozadju) in zaide, ko prestopimo mejo iz svetlega v temno (na Sliki 2 v ospredju). Ta meja, se seveda vrti okoli pravokotnice na ekliptiko s kotno hitrostjo, ki ustreza kroženju Zemlje okoli Sonca. Vsak dan se torej meja nekoliko premakne, in sicer v istem smislu kot je lastno vrtenje Zemlje. Poleg tega še opazimo, da je frekvenca rotiranja Zemlje okoli svoje osi tolikšna, da Zemlja v 24 urah naredi več kot le en obrat. Zemlja mora namreč v enem letu opraviti en obrat več, kot doživimo na Zemlji dni. Če se na primer Zemlja ne bi vrtela, bi v enem letu doživeli le en dan in eno noč (primerjaj s Sliko 1). Če bi Zemlja v enem letu naredila ravno en obrat okoli svoje osi v smeri zahod-vzhod, na ekvatorju sploh ne bi doživeli sončnega vzhoda ali zahoda. En obrat Zemlje se torej izniči z navideznim premikanjem meje med nočjo in dnevom. Če torej leto na Zemlji traja 365,24 dni, tedaj Zemlja v 24 urah opravi 1+1/365,24 obrata.

Opazujmo sedaj, kako se spreminja ura sončnega zahoda. Pomembno pri tem je, za kolikšen kot se premakne točka na Zemeljski površini (naša opazovalnica) v 24 urah (naredi 1+1/365.24 obrata, torej se efektivno premakne za 1/365.24 obrata) in pa za koliko se v tem času premakne meja med nočjo in dnevom. Opazujemo seveda točko, kjer ta meja seka črtkano ravnino na sliki2. Zanima nas za koliko se to sekališče premakne v 24 urah. Če se sekališče premakne za več kot 1/365.24 obrata, smo po 24 urah še vedno v osvetljenem področju, torej se je dan podaljšal, medtem ko, če se sečišče premakne za manj kot 1/365.24 obrata, tedaj je naša opazovalnica že v temnem predelu, dan se je skrajšal.

V pol leta opravi meja med dnevom in nočjo ravno polovico obrata okoli pokončne osi. Vendar pa to pomeni veliko večji kot okoli lastne osi Zemlje, ki ga naredi meja sončnega zahoda (na Sliki 2 v ospredju) med zimskim in poletnim solsticijem (na Sliki 4 rjav del), kot ga ta ista meja opravi med poletnim in zimskim solsticijem (na Sliki 4 rumen del). Ravno obratno seveda velja za mejo sončnega vzhoda (na Sliki 2 v ozadju). Med zimskim in poletnim solsticijem se torej sečišče, ki določa sončni zahod, premakne v 24 urah bolj kot pa naša opazovalnica, dan se torej podaljša. V tem času se meja sončnega vzhoda seveda premakne manj kot 1/365.24 obrata dnevno, sonce torej z vsakim dnem prej vzide.

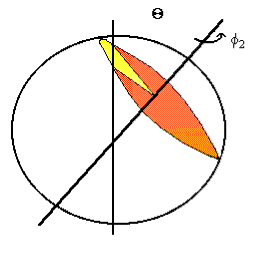
Kateri od obeh, zgodnejše vzhajanje Sonca ali kasnejši zahod, podaljša dan za več minut, seveda ne moremo ugotoviti kar tako, z mahanjem rok, kot smo to lahko počeli do tega trenutka. Podrobnejši račun (glej dodatek) nam da transcendentno zvezo med (kotom zasuka meje) in , iz katere lahko izračunamo vzhod in zahod Sonca. Seveda le numerično, kar je seveda primerno za napoved sončnega gibanja, nikakor pa nam ne pomaga pri sami razlagi.

Zlahka pa lahko razložimo, zakaj se dneva z najzgodnejšim sončnim zahodom in najkasnejšim sončnim vzhodom ne ujemata. Sonce zaide najbolj zgodaj tedaj, ko je dnevni zasuk meje sončnega zahoda in naše opazovalnice enak, medtem ko je najkasnejši sončni vzhod tedaj, ko se ujemata zasuk meje sončnega vzhoda in naše opazovalnice. Ker sta hitrosti premikanja mej sončnega zahoda in sončnega vzhoda v določenem trenutku različni (glej Sliko 3 – med zimskim in poletnim solsticijem je povprečna kotna hitrost meje sončnega zahoda manjša kot v drugi polovici leta, medtem ko velja za sončni vzhod ravno obratno), bosta tudi dneva, ko se le ti ujemata z vrtenjem Zemlje okoli lastne osi ob različnih časih. Zimski solsticij je tako 21. decembra, medtem ko je dan z najzgodnejšim sončnim zahodom okoli 10. decembra, dan z najkasnejšim sončnim vzhodom pa okoli 31. decembra. Razliki do solsticija morata biti seveda enaki, dokler obravnavamo ekliptiko kot krožnico (razmisli zakaj?). To tudi pojasni, zakaj se čas sončnega vzhoda na začetku januarja skoraj ne spreminja (smo le nekaj dni po dnevu z najkasnejšim sončnim vzhodom, dnevna zasuka meje sončnega vzhoda in naše opazovalnice sta skoraj enaka), medtem ko so večeri že občutno daljši (razlika dnevnih zasukov je tu že večja).

Ravno obratna situacija je pri poletnem solsticiju 21. junija. Tu imamo dan najkasnejšega sončnega zahoda okoli 30. junija, medtem ko je dan najzgodnejšega sončnega vzhoda že okoli 11. junija. Razlogi za to so seveda povsem analogni kot zgoraj.

Morda še to, kje se bo poznala sploščenost ekliptike (le ta je namesto krožnica, v resnici elipsa), pri obravnavi gornjega pojava. Za samo razumevanje pojava le ta ni bistvena, seveda pa bo vstopila v kvantitativne izračune. Za asimetrijo pri maksimalnih časih sončnih vzhodov in zahodov je namreč bistveno gibanje Zemlje v bližini dneva poletnega ali zimskega solsticija. Tu lahko gibanje približno opišemo s krožnico (pritisnjena krožnica ji rečemo). Če torej ne bomo gledali predaleč stran od dneva D, bo vse tako kot smo opisali za popolno krožnico. Sploščenost seveda ni povsem brez posledic. Zaradi nje dan najzgodnejšega (najkasnejšega za poletni) sončnega zahoda in najpoznejšega sončnega vzhoda ne bosta povsem simetrično oddaljena od zimskega solsticija in jo v resnem računu seveda moramo vzeti v okvir.

Glej tudi:
Stran o analemi (osmici, ki jo nariše tekom leta sonce na nebu) in pojasnilo z njeno pomočjo
Zapis o Enačbi časa na straneh Greenwichškega observatorija

Dodatek: Izpeljava formule za izračun dolžine dneva (pri krožni ekliptiki)

Enačba ravnine, ki seka kroglo na geografski širini je , kjer je normala na ravnino oz. os rotacije. Krajevni vektor zapišem v obeh sistemih (v sistemu 1 je z os normala na ekliptiko, v sistemu 2 pa os rotacije)

Z izenačenjem obeh enačb dobimo:

Tu sta , kjer je krožna frekvenca vrtenja okoli Sonca, medtem ko je krožna frekvenca vrtenja okoli svoje osi. Iz zgornje enačbe torej dobimo sečišča z ravnino meje med dnevom in nočjo, to je zaporedoma sončne vzhode in zahode.

(Jure Zupan)

-