Iz mladih let se spomnim, da obstajata dva modela atmosfere: adiabatni in izotermni. Kateri je boljši približek realni atmosferi, oziroma drugače: Po kakšni funkciji pada zračni tlak z višino?
Pa si poglejmo oba modela atmosfere, ki ju omenja vprašanje. Začnimo kar pri običajni plinski enačbi za idealen plin, ki jo nekoliko predelamo v obliko
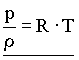
kjer je
gostota plina (v našem primeru zraka), p je tlak plina in T temperatura, ter R plinska konstanta. Vse troje se s temperaturo spreminja, pri čemer je tlak na višini H ravno tolikšen, da uravnoteži silo težnosti vseh plasti nad to višino. Tlak se bo torej, če se premaknemo v za majhno višinsko razliko dz višje ležečo plast zraka, za toliko zmanjšal, za kolikor je manjša sila teže, ki pritiska nanjo. Ob uporabi plinske enačbe (za gostoto smo vstavili gornji izraz iz plinske enačbe) tako dobimo
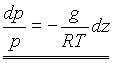
kjer je g težni pospešek. Če bi poznali, kako se spreminja tlak s temperaturo, bi lahko gornjo enačbo rešili in dobili višinski potek tlaka v atmosferi. Da pridemo do te zveze pa se moramo poslužiti novih predpostavk. Najenostavnejša sta naslednja primera:
1) Izotermni model
V tem primeru predpostavimo, da se temperatura z višino ne spreminja T = konst. V tem primeru lahko gornjo difenecialno enačbo za odvisnost tlaka od višina enostavno razrešimo in dobimo
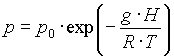
Tlak torej eksponento pada z višino H z neko specifično razpolovno konstanto, ki je odvisna od temperature, ni pa odvisna od vrste plina. Zaradi eksponentnega pojemanja tlaka le ta nikoli ne pade na nič. Atmosfera se tako razteza neskončno daleč v vesolje, seveda pa je dovolj daleč zanemarljivo majhna.
Velja poudariti, da ta enačba od modelov, ki jih bomo obravnavali tu, najmanj natančno opisuje realne razmere, kajti v resnici se temperatura zemeljske atmosfere zelo intenzivno spreminja z višino.
2) Adiabatni model
V tem modelu predpostavimo, da zrak, ko se premika od ene plasti zraka do druge ne izmenja pri tem toplote z okolico. Seveda je ta predpostavka vprašljiva v primeru realnega ozračja, kjer imamo močne tokove zraka (veter) in s tem v večini primerov nestacionarne razmere. Vendar pa nam da ta približek kljub vsemu nekoliko realnejšo sliko atmosfere, ima pa pri tem tudi svoje omejitve, kot bomo videli.
Za adiabatno spremembo plina velja
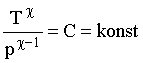
kjer je 
eksponent adiabate (za zrak je ta =1.4). Z uporabo te zveze pridemo do naslednje odvinosti tlaka od višine
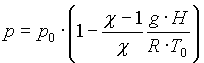
Kot vidimo se v adiabatni atmosferi tlak linearno manjša z višino od začetnega p0 do nič. Atmosfera v tem modelu ima jasen rob! Po določeni višini je tlak enak nič, nad to mejo ni več atmosfere.
Iz opazovanj pa vemo, da takšnega ostrega roba ni, tudi adiabatna atmosfera, kot smo že pričakovali ni povsem zvesta slika realne atmosfere.
3) Meteorološki model
V meteorologiji se poslužujejo eksperimentalne enačbe spreminjanja temperature z višino:
kjer je T0 temperatura pri tleh, medtem ko je b=3 10-5 m-1 konstanta, ki popiše spreminjanje temperature z višino (približno 1 stopinja na 100m).
Za spreminjanje tlaka sedaj sledi
Tudi ta enačba boleha za podobno boleznijo, kot adiabatni model, saj tlak na določeni višini pade na nič. Atmosfera ima zopet rob, vendar pa je tu odvisnost tlaka od višine potenčna in ne več linearna.
Z upoštevanjem višjih členov v razvoju odvisnosti temperature od višine (to je kvadratične in ostale višje člene) lahko zelo natančno določimo temperaturo in s tem tlak na poljubni višini.
V zaključki naj povzamem, da natančnega modela za zemeljsko atmosfero (še) ni, ampak se poslužujemo bolj ali manj natančnih približkov. Predvsem sta razširjena izotermni in adiabatni model, zaradi enostavnosti računanja, vendar pa dokaj slabo opisujeta realne razmere. Izotermni model je praktično popolnoma neuporaben že za malo večje višinske razpone (prek 500 m), saj temperatura zraka močno pada z višino in nikakor ni konstantna!
Adiabatni model je nekoliko boljši približek, vendar pa predpostavka o neizmenjavanju toplote med plastmi zraka ne drži povsem. Toplota se namreč prenaša med zemljo, zračnimi plastmi in vesoljem v obliki sevanja, konvekcijskih tokov,….
Znatno boljši je meteorološki model atmosfere, ki je določen eksperimentalno prek meritev temperature in iskanjem ustrezne funkcijske odvisnosti. Vendar tudi ta opisuje le povprečno odvisnost tlaka od višine. Krajevno spreminjanje, ki nam kroji vreme, pa zahteva drugačne računske postopke. Manj analitičnih poti in več numeričnega računanja.
(Boštjan Bezenšek in Jure Zupan)
