Luna je približno 400-krat manjša od Sonca, a ker je Zemlji tudi 400-krat bližje, je njena navidezna velikost na nebu približno takšna kot Sončeva. Luna na svoji poti okrog Zemlje vsak mesec pride med Zemljo in Sonce – pravimo, da je v mlaju. Vendar z Zemlje ne vidimo vsak mesec Sončevega mrka. Največkrat nevidna Luna zdrsne nad ali pod Soncem oziroma njena senca preleti pod ali nad Zemljo. Le v redkih primerih, ko so vsa tri telesa poravnana na isti premici, pade na Zemljo Lunina senca ali polsenca. V krajih, kjer na Zemljo pade senca, vidijo popolni Sončev mrk, v krajih, kjer pade le polsenca, pa vidijo delni Sončev mrk.
Senca in polsenca
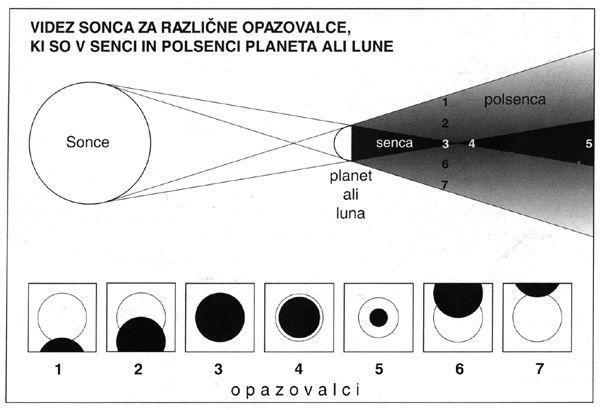
Vsa telesa, ki so obsijana s svetlobo, mečejo senco in polsenco. Planete in njihove sateli-te osvetljuje Sonce. Senca, ki jo meče planet ali luna, ima obliko stožca z osnovno ploskvijo ob planetu. Polsenca ima obliko prisekanega stožca. Senca in polsenca ležita vedno na zveznici med Soncem in planetom. Če stojimo na primer v planetovi senci, ne vidimo Sonca. Če se pomaknemo na rob med senco in polsenco, vidimo čisto majhen delček Sonca. Ko potujemo naprej proti robu polsence, se nam odkriva vedno večji del Sonca. Vrh sence je vedno v tisti točki, kjer je navidezna velikost planeta ali lune enaka navidezni velikosti Sonca. Za večjim planetom je torej daljša senca kot za manjšim, če sta oba enako oddaljena od Sonca. To lahko ponazorimo z Luno in Zemljo, ki sta obe približno enako oddaljeni od Sonca. Lunina senca je v povprečju dolga 375.000 kilometrov (premer Lune je 3480 kilometrov), Zemljina pa se razteza do oddaljenosti 1.460.000 kilometrov (premer Zemlje je 12.760 kilometrov). Iz slike levo pa lahko vidimo, da bolj ko je planet oddaljen od Sonca, daljša je njegova senca. Tako je za Venero, ki je bližje Soncu in je približno tako velika kot Zemlja (premer 12.100 kilometrov), “le” 950.000 kilometrov dolga senca.
Za polsenco pa iz slike levo hitro ugotovimo, da je večja, če je planet večji in če je bližje Soncu. Na sliki vidimo, da tudi opazovalec številka 5 stoji v senci planeta. Vendar pa je v tem primeru navidezna velikost planeta mnogo manjša od Sonca. V tem primeru ne govorimo o mrku, temveč o prehodu planeta čez Sončevo ploskvico. 7. junija 2004 se bodo Sonce, Venera in Zemlja znašli na isti premici. Na sliki bi torej namesto planet ali luna napisali Venera, Zemlja pa bo na mestu opazovalca številka 5. Tega dne bomo lahko videli prehod Venere čez Sončevo ploskvico. S senco in polsenco se amaterski astronomi srečamo tudi pri )upitru, ko lahko opazujemo sence Galilejevih satelitov pri potovanju čez ]upitrovo ploščico ali vzhajanje satelitov izza ]upitra oziroma bolje rečeno prihod satelitov iz Jupitrove sence. Še bolj dramatično pa je naše srečanje z Zemljino senco in polsenco med Luninimi mrki in Lunino senco in polsenco med Sončevimi mrki.
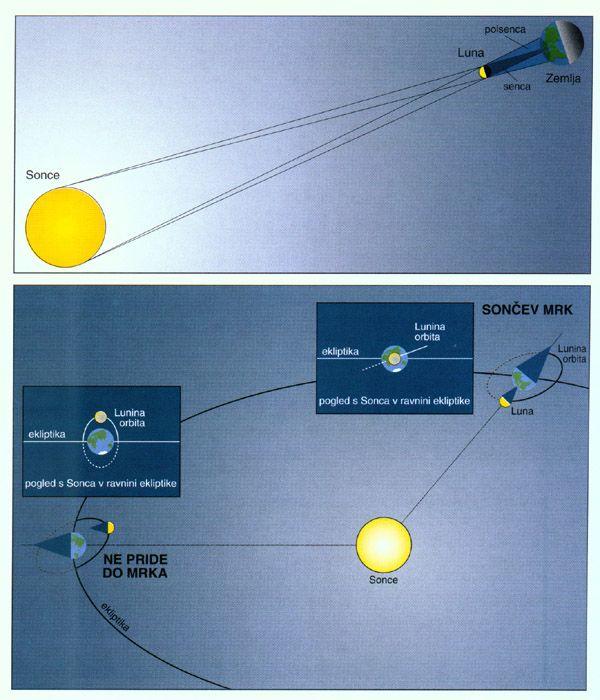
Luna kroži okrog Zemlje, obe skupaj pa okrog Sonca. Lunina orbita je za 5 stopinj nagnjena na ravnino
ekliptike in jo torej seka v dveh točkah. Presečišču rečemo vozel. Vsakih 29 dni pride Luna med Zemljo
in Sonce, pravimo, da je v mlaju. Ker pa Luna med kroženjem okrog Sonca ohranja lego svoje orbite v
prostoru, le dvakrat na leto (v razmiku pol leta) pride v položaj, ko je točno med Soncem in Zemljo.
Sončev mrk
Kot smo zapisali že v uvodu, gre pri Sončevih mrkih za geometrijo Lunine sence in polsence. Pri popolnem Sončevem mrku na Zemljo padeta Lunina senca in polsenca, pri delnem pa le polsenca. Sončev mrk (delni ali popolni) lahko torej nastopi le takrat, ko so na isti premici poravnani Sonce, Luna in Zemlja oziroma ko sta Luna in Sonce na istem delu neba (gledano z Zemlje). Sonce navidezno potuje po ekliptiki. Lunina tirnica pa je nagnjena za 5,1 stopinje na ekliptiko in jo seveda seka v dveh točkah, ki jima rečemo vozla. Točka, kjer Luna prečka ekliptiko na svoji poti proti severu, se imenuje dvižni vozel, ko gre proti jugu pa padni vozel. Do mrka lahko pride le takrat, ko sta Sonce in Luna v bližini vozlov. Če bi bila Sonce in Luna točkasti telesi, bi do mrka lahko prišlo le takrat, ko bi bila in Sonce in Luna natančno v vozlu. Ker pa imata obe telesi svojo navidezno velikost, ki je okrog pol stopinje, pride do mrkov (delnih) tudi takrat, ko sta obe telesi v bližini vozlov (slika spodaj).
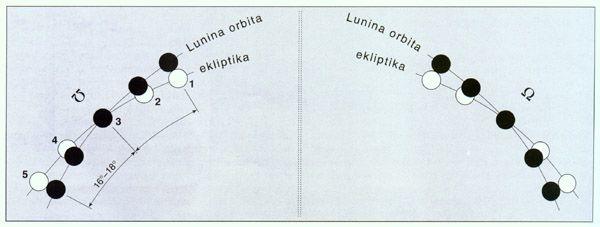
Del ekliptike, kjer lahko pride do mrkov, leži v bližini vozlov, kjer Lunina orbita seka ekliptiko. Sonce
se na delu poti od točke 1 do 5 zadržuje enkrat na leto približno 34 dni, Luna pa vsak mesec to pot
prepotuje v približno treh dneh. V mislih si lahko sliko predstavljamo dinamično: če je Sonce na
primer v točki 2, ko mimo pripotuje Luna, bomo videli delni Sončev mrk, če je v točki 3, bomo videli
popolnega… Povsem enako je dogajanje v okolici drugega vozla, kjer je Sonce pol leta kasneje.
Sonce prepotuje ekliptiko v enem letu, torej je dvakrat na leto v bližini vozlov. Dolžina poti okoli enega vozla, na kateri lahko pride do mrka, je približno 34 stopinj, to pot pa Sonce prepotuje v mesecu in nekaj dneh. Če v tem času mimo pripotuje Luna (kar se zagotovo zgodi), lahko nekje na Zemlji vidimo mrk (delni ali popolni). Zato sta z Zemlje (s kateregakoli kraja) ponavadi vidna vsaj dva Sončeva mrka na leto. Vozla sta pol leta narazen, zato trenutno do mrkov prihaja (grobo rečeno) februarja in avgusta.
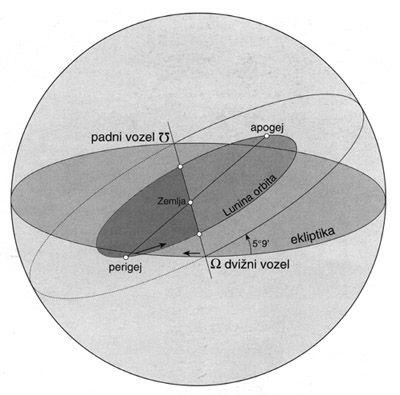
Lunina tirnica pa ni stalna. Zaradi gravitacijskega vpliva Sonca nagnjenost tira niha med 4°58′ in 5°19′ (trenutno je 5°9′). Točki Luninega perigeja in apogeja se vrtita z obhodnim časom 8,85 leta, črta vozlov pa potuje po ekliptiki v retrogradni smeri z obhodnim časom 18,61 leta (pojavu pravimo nutacija). Zato se tudi meseci, v katerih lahko pride do mrkov, zavrtijo naokrog v obdobju 18,61 leta. Tako so mrki v letu 1990 nastopali (grobo) januarja in julija, v letu 1995 maja in oktobra…
Potek mrka – prvi stik…
Lunino lastno gibanje (zaradi kroženja okrog Zemlje) je od zahoda proti vzhodu, zato se ob mrkih vedno dotakne Sonca na njegovem zahodnem robu. Temu trenutku pravimo prvi stik. Ponavadi ga s prostim očesom ne vidimo, če imamo natančne podatke za opazovališče (čas in kot prvega stika), pa ga lahko kmalu opazimo s teleskopom. Po prvem stiku Luna počasi leze čez Sonce (v resnici opazujemo njeno lastno gibanje) in ga vedno bolj zakriva. Trenutku, ko je prekrito vse Sonce, pravimo drugi stik. Začne se popolna faza mrka. Konec popolne faze je takrat, ko se Luna s svojim zahodnim robom dotakne zahodnega roba Sonca. Kmalu po tem izza Lune pogleda rob Sonca. Temu trenutku rečemo tretji stik. Luna nato počasi odkriva večji in večji del Sonca. Trenutku, ko Luna zapusti Sončevo ploskvico, rečemo četrti stik.
Tak potek mrka je le v krajih, kjer lahko vidimo popolni mrk. Tam, kjer lahko vidimo le delnega, pa pride samo do prvega in četrtega stika.
Kot smo lahko videli na slikah v prejšnjem prispevku, potujeta Lunina senca in polsenca po površju Zemlje po zapleteni krivulji. Poti, po kateri potuje senca, pravimo centralna (osrednja) črta mrka. Nad to črto se Luna dotakne Sonca na njegovem jugozahodnem robu, pod njo pa na severozahodnem robu. Na spodnji sliki je prikazan potek namišljenega mrka za različne opazovalce na Zemljinem površju. Pri letošnjem mrku bi bil opazovalec številka 1 nekje na skrajnem severu Zemlje, opazovalec številka 2 na primer v Skandinaviji, opazovalec 3 na centralni črti mrka, opazovalec 4 v Španiji, opazovalec številka 5 pa nekje sredi saharske Afrike. Lunina senca potuje po prostoru po skoraj ravni črti. Njena pot postane nenavadno zavita šele takrat, ko naleti na naš okrogel planet, ki se za povrhu še vrti okrog svoje osi.
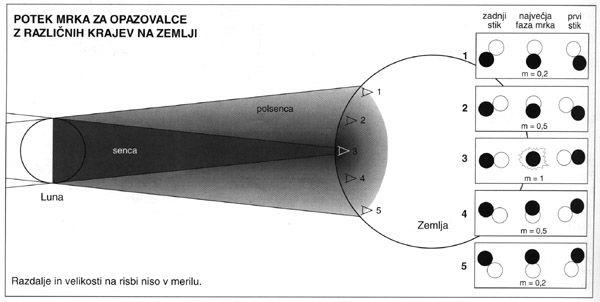
Magnituda mrka
Največja stopnja prekritja Sončeve ploskvice med popolnim ali delnim mrkom se imenuje magnituda mrka. Podatek, ki nima nič skupnega z navidezno svetlostjo zvezd, nam pove, kolikšen del Sončevega premera je prekrila Luna (in ne, kolikšen del površine Sonca je zakrite!). Lahko bi rekli, da z magnitudo mrka povemo relativno globino Luninega “ugriza”.
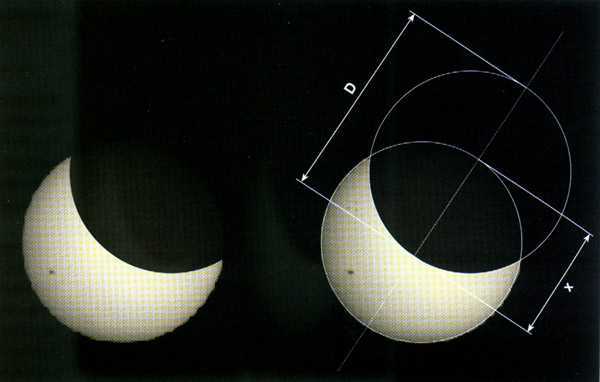
Magnitudo Sončevega mrka lahko določimo iz fotografije ali risbe z ravnilom in šestilom.
Iz fotografij ali risb delnega mrka zelo enostavno določimo magnitudo tako, da zakriti del premera Sonca delimo s celotnim premerom Sonca:
magnituda mrka = x / D
pri čemer x in D izmerimo na sliki ali risbi. Zanimiva, a nekoliko težja matematična naloga je računanje zakritosti Sončevega površja ob posameznih fazah mrka. Kolikšno je razmerje med magnitudo mrka in zakritostjo Sončeve ploskvice, si lahko ogledamo na spodnji sliki.

Pri delnih mrkih nam magnituda torej pove, kolikšen premer Sonca bo prekrila Luna. Pri popolnih mrkih pa nam magnituda pove, kolikokrat je navidezni premer Lune večji (ali manjši pri kolobarjastih mrkih) od Sonca. Letošnji mrk bo popolni Sončev mrk, Luna pa bo 1,0147-krat (navidezno) večja od Sonca.
Videz mrka
Zemlja se giblje okoli Sonca po elipsi, zato ni vedno enako oddaljena od njega. Navidezni premer Sončeve ploskvice na nebu se nenehno spreminja. Največji je okrog 3. januarja, ko je Zemlja Soncu najbližje (v periheliju), najmanjši pa je okrog 6. julija, ko je Zemlja najbolj oddaljena od Sonca (v afeliju). Tudi Lunina tirnica okrog Zemlje je elipsa, zato tudi Luna nima vedno enakega navideznega premera. Največji je ob perigeju, ko nam je Luna najbližje, najmanjši pa ob apogeju, ko je najdlje. Tako se lahko zgodi, da je Lunina ploskvica ob popolnem mrku navidezno večja od Sončeve, enaka ali pa manjša. V prvem in drugem primeru govorimo o popolnem Sončevem mrku, v tretjem pa o kolobarjastem Sončevem mrku, saj izza roba Lune gleda tanek obroč Sonca. Seveda pa so možne vse medsebojne kombinacije, ki vplivajo na videz in trajanje popolne faze mrka.
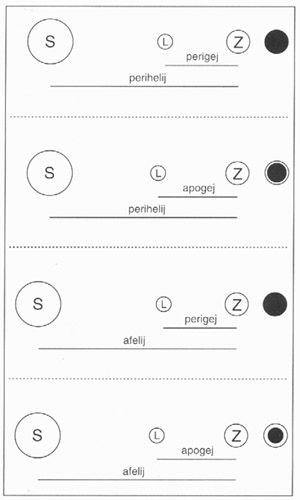
Na začetku prispevka smo omenili, da je Lunina senca v povprečju dolga 375.000 kilometrov. V najbolj ugodnem primeru, ko je Zemlja v afeliju, Luna pa v perigeju, je dolžina sence 380.000 kilometrov. Najkrajša pa je senca v primeru, ko je Zemlja v periheliju, Luna pa v apogeju. Takrat je njena dolžina 367.000 kilometrov. Povprečna razdalja med Luno in Zemljo je 384.000 kilometrov. Pri teh številkah seveda ne smemo prezreti dejstva, da je oddaljenost med Zemljo in Luno mišljena kot oddaljenost med središčema teh dveh teles. Ker Lunina senca pade na površje Zemlje, se lahko v najbolj ugodnem primeru, ko pade v bližino ekvatorja, zgodi, da je razdalja za Zemljin polmer (približno 6370 kilometrov) krajša.
Iz povedanega lahko sklepamo, da največkrat pade na Zemljo zelo ozek del sence pri vrhu stožca, in še to največkrat tisti del, ko vidimo kolobarjast Sončev mrk. Tudi v primeru, ko vidimo popolni mrk, ni senca nikoli širša od 269 kilometrov. Pri letošnjem mrku, ko bo Zemlja približno mesec dni po afeliju, Luna pa tri dni po perigeju, bo širina sence, ki bo padla na srednje geografske širine, le 112 kilometrov. Polsenca je seveda mnogo širša. Delne faze mrka lahko zato vidimo na območjih, ki so do nekaj tisoč kilometrov oddaljena od sence.
Trajanje popolne faze mrka
Trajanje popolnega mrka določajo štirje glavni dejavniki. Predstavljeni so na časovnem diagramu desno, ki je neke vrste superkoledar mrkov od leta 1982 do leta 2010. Spodaj (od leve proti desni) tečejo dnevi oziroma meseci, navpično pa si sledijo leta. Sončevi mrki so vrisani na njihovih pravih datumih. Zraven vsakega mrka je naveden največji čas trajanja v minutah in sekundah, delni mrki so označeni le s črko D.
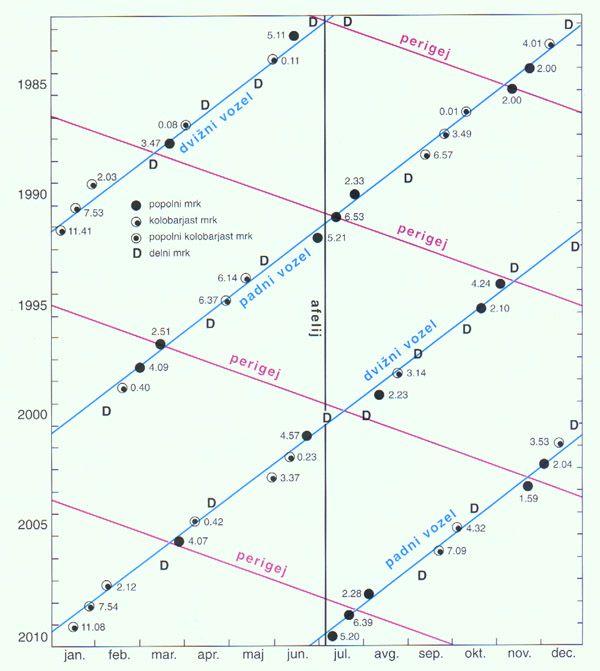
Sončevi mrki na “superkoledarju”, kjer meseci tečejo od leve proti desni, leta pa od zgoraj navzdol. Do
mrkov pride okoli datumov, ko Sonce prečka vozle Lunine orbite (modre črte). Najdaljši popolni mrk
nastopi okoli datuma Luninega perigeja (rdeče črte) in Zemljinega afelija (črna navpična črta). Najdaljše
trajanje popolnega mrka je napisano zraven simbola v minutah in sekundah. Podatke smo vzeli iz
knjige Canon of Solar Eclipses -2003 to +2526.
Kot smo že omenili je prvi pogoj ta, da mora mlaj nastopiti, ko se Luna nahaja blizu enega od obeh vozlov svoje orbite. Vozla sta točki na nebu, kjer Luna prečka ekliptiko, to je pot Sonca. Tudi Sonce mora biti takrat v bližini vozlov. Modre diagonalne črte nam pokažejo dva datuma vsako leto, ko Sonce prečka Lunine vozle. Vsi mrki ležijo blizu teh črt. Bližje ko je mrk vozlu, bolj natančno so poravnani Sonce, Zemlja in Luna. V tem primeru pade senca na Zemljo do 6000 kilometrov bližje kot v primeru, ko le oplazi Zemljin rob. Povedano drugače, “izbočenost” našega planeta nas pripelje za približno 6000 kilometrov bližje Luni, kadar jo vidimo v bližini zenita, kot kadar je na horizontu. Posledica tega je, da je senca večja in mrk daljši. V praksi to pomeni, da so najboljši (najdaljši) mrki tisti, ki nastopijo okoli poldneva v tropskih krajih.
Drugi pomemben dejavnik je Lunina spremenljiva oddaljenost od Zemlje. Kot smo videli, je v povprečju Luna od nas preveč oddaljena, da bi njena senca sploh dosegla Zemljino površje, zato je večina centralnih Sončevih mrkov kolobarjastih, na pa popolnih. Najdaljši popolni mrk nastane, kadar je Luna najbližje Zemlji, se pravi blizu svojega perigeja. Rdeče diagonalne črte kažejo datum vsakega leta, ko Sonce prečka točko Luninega perigeja na našem nebu. V bližini, kjer se sekajo rdeče in modre črte, lahko vidimo dolge popolne mrke. Na diagramu vidimo, da presečišča padejo v mesece februar-marec, junij-julij in oktober-november.
Tretji dejavnik, ki vpliva na dolžino mrka, je oddaljenost Zemlje od Sonca. Dlje kot je Sonce, manjša je videti njegova ploskvica, dalj časa ga lahko Luna prekriva. Zemlja je vedno najdlje od Sonca, ko je v afeliju, to je okoli 4. julija. Zato najdaljši popolni mrki nastopijo v juniju in juliju. Črna črta na diagramu označuje letni datum afelija.
Ko se vse tri črte sekajo, lahko pride do mrka izjemne dolžine. Seveda pa mora biti izpolnjen še četrti pogoj. Namreč, da je mrk okoli tega datuma – kar seveda sploh ni nujno!
Na prvi pogled se zdi, da so na diagramu znaki za mrke raztreseni brez reda ob modrih črtah vozlov in da zadenejo ali zgrešijo presečišča črt povsem po naključju. Pa ni tako! Datumi mrkov se strogo ravnajo po 18-letnih ciklih, ki ji poznamo pod imenom saros. Ker se mrki pojavljajo pogosteje kot enkrat na 18 let, je vedno v teku več sarosov hkrati. V 20. stoletju smo imeli srečo, da je ena od trenutnih serij prinesla mrke ravno v čas junij-julij in zelo blizu padnega vozla:
| 1919 | maj 29 | 6m 51 s |
| 1937 | junij 8 | 7m 04s |
| 1955 | junij 20 | 7m 08s |
| 1973 | junij 30 | 7m 04s |
| 1991 | julij 11 | 6m 53s |
| 2009 | julij 22 | 6m 39s |
| 2027 | avgust 2 | 6m 23s |
| 2063 | avgust 14 | 5m 49s |
Mi se bomo morali letos zadovoljiti z 2 minuti in 27 sekund dolgo popolno fazo.
Opis geometrije mrka je zahtevna in nehvaležna naloga. Za pojav, pri katerem sodelujejo tri telesa v prostoru, od katerih se dve neprestano gibljeta, imamo na voljo statične dvodimenzionalne slike. Upamo pa, da smo vsaj približno pojasnili nastanek Sončevih mrkov, in da si boste po objavljenih slikah lahko predstavljali dogajanje v naravi.