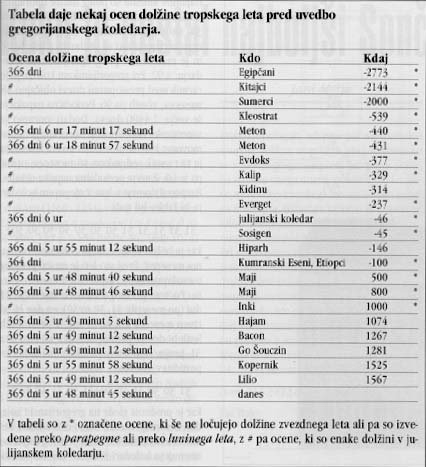
Nenavadna ironija je, da je 22. (24.) februarja 1582 v znamenju Rib v Hiparhovem rojstnem kraju Nikeji, ko so bili Snell, Kepler, Galilei, Dominis, Bruno in Brahe po vrsti stari 2, 11, 18, 22, 34 in 36 let, krščanska Cerkev naredila astronomiji pravo malo sramoto in na pobudo papeža Gregorja XIII. uvedla gregorijanski koledar, da bi s tem pokrila 10-dnevno razliko, ker je božič nastopal vedno pozneje. Čeprav so uvedbo novega koledarja dolgo pripravljali, ni nikakor opravičila ponesrečenih ciljev, ki so jih vodili, saj je bil ta težak problem in eden najstarejših že 508 let uspešno rešen. Lotil se ga je, kot že mnogi pred njim in na mnogih mestih, perzijski pesnik, astronom, matematik in filozof Gijasuddin Hakim Omar (tudi ‘Umar) Abulfath Ibn bin Ibrahim an-Nišapuri Hajam. Rodil se 31. marca 1048 v Najšaburju ali v neki vasi blizu Najšaburja v pokrajini Horasan. Bil je tadžikiškega porekla.
Omar Hajam
Omar Hajam (avtor JM)Vzhod Hajama slavi kot astronoma, zahod pa kot pesnika-filozofa. Na dan njegovega rojstva je bilo Sonce v tretji stopnji Dvojčkov. To dejstvo je uporabil indijski hajamolog Govindi, da je določil natančen datum rojstva. Ker so tedaj zelo pazili na razpored zvezd pri rojstvu, so zabeležili tudi položaj Sonca glede na Jupiter in Zemljo. V svoji knjigi Dopolnitev čuvarjev modrosti (Tetima Sivan el-hikma) je perzijski zgodovinar in biograf Abulhasan Ibrahim ben Muhammed al-Bajhaki (umrl 1170) zapisal:
“Hajamovo rojstno znamenje sta bila Dvojčka. Sonce in Merkur sta bila v tretji stopnji Dvojčkov. Merkur je bil v konjunkciji, Jupiter pa se je nahajal v trigonalnem odnosu z Dvojčkoma.” Da je lahko Govinda natančno določil dan in leto njegovega rojstva, je mnogo let preučeval astronomske tabele svojega časa. V veliko pomoč so mu seveda bile znane Malikšahove tabele, ki jih je sestavil Hajam, in takrat še niso bile izgubljene.
Hajamova družina je bila verjetno dokaj premožna, da mu je lahko omogočila dobre učiteje. Mnogo virov priča o tem, da je v svojih mladih letih dobil solidno izobrazbo. Beseda hajam v arabskem jeziku označuje človeka, ki tke blago in izdeluje šotore. Tkanje šotorov je bil poklic njegove družine. Po vsej verjetnosti bi tudi on, prav tako kot njegov oče, to počel, če se ne bi pojavil dobrosrčen človek Abu Tahir, glavni sodnik v Samarkandu, ki je v mladem Hajamu odkril izreden talent in mu omogočil gmotno pomoč, da je obiskoval šolo in se temeljito izobrazil. Mnogo perzijskih pesnikov je na podoben način prevzelo svoja imena iz poklicev svojih družin. Sam Hajam je namignil na svoje ime v naslednjih muhastih vrsticah:
Hajam, ki šiva šotore znanosti,
je padel v talilno peč potrtosti in na hitro zgorel;
škarje Usode so porezale šotorske vrvi njegovega življenja
in prekupčevalec Upanja ga je zastonj prodal!
Pripravljalne in druge znanosti je tako poslušal v svojem rojstnem kraju. V tistem času je bilo najšabursko vseučilišče na dobrem glasu. Na njem je predaval profesor pobožni Imami Mowaffak, ki je kot učenjak slovel po celem Vzhodu. Nenavadno dejstvo je, da lahko najdemo najpristnejši življenjepis miroljubnega Hajama, katerega največje prizadevanje je bilo na široko razširiti spoznanja znanosti, v delu Zgodovina morilcev perzijskega zgodovinarja Mirkhonda (1443-1498). V njem najdemo zapis, ki ga je napisal Ebul-Kasim: “Eden najbolj učenih mož Horasana je bil Imami Mowaffak iz Najšaburja, zelo spoštovan in čaščen mož – naj Bog razveseli njegovo dušo. Prekoračil je 85. leta in vsi so verjeli, da bo vsak deček, ki bo bral Ku’ran ali v njegovi navzočnosti preučeval običaje, dosegel spoštovanje in srečo. Zaradi tega me je oče poslal iz Tusa v Najšabur skupaj z Abdu-samadom, doktorjem prava, da bi se učil pod vodstvom tega slavnega učitelja. Bil mi je naklonjen in prijazen. Kot njegov učenec sem čutil do njega veliko ljubezen in vdanost in sem tako preživel štiri leta ob njegovih uslugah. Ko sem prvič prišel tja, sem spoznal še druga dva učenca svojih let, ki sta tudi pravkar prišla, Hakim Omar Hajama in Ben as-Sabbaha. Oba sta bila obdarjena z bistrostjo in najvišjimi nravnimi močmi. Vsi trije smo postali dobri prijatelji. Ko je Imami končal s predavanji, sta se mi pridružila in smo jih ponavljali. Omar je bil doma iz Najšaburja, medtem ko je bil oče Hasana Ben as-Sabbaha, Ali po imenu, strog človek, vendar heretičen v svojem verskem prepričanju in doktrini. Nekega dne je rekel Hasan meni in Hajamu: “Vsi verjamejo, da bodo učenci Imamija Mowaffaka dosegli srečo in bogastvo. Če vsi trije tega ne bomo dosegli, eden od nas bo to prav gotovo. In kaj bo potem naša skupna zaprisega in obveza?” Odgovorila sva: “Naj bo, kot želiš.” “Dobro,” je odgovoril, “prisezimo, da bo tisti, ki bo dosegel srečo in bogastvo, to delil enakovredno z drugima dvema in ne bo zahteval preveč zase.” “Naj bo tako,” sva oba odgovorila in tako smo si s temi besedami drug drugemu zaobljubili. Leta so tekla in jaz sem odšel iz Horasana v Transoksanijo (današnji Kazahstan) in potoval v Gasno in Kabul. Ko sem se vrnil, sem začel opravljati administrativna dela za časa sultanata sultana Alp Arslana.”
Ebul-Kasim je prvi prišel do visokega položaja. Prišel je na seldžuški dvor in med vladanjem sultana Muhamed ben Da Ud Alp Arslana Junaka-leva (1030-1072) postal prvi vezir. Seveda nista ne Hajam ne as-Sabbah izpustila priložnosti. Obrnila sta se na svojega nekdanjega tovariša in ga spomnila na dijaško zaprisego. Prišla sta k njemu in terjala svoj delež. Ebul-Kasim, ki je kot vezir dobil naziv Nizamul al-Mulk (državni red), je bil radodaren in je držal svojo besedo. Hajamu je ponudil vidnejše mesto na dvoru. Skromni učenjak in pesnik ga ni hotel sprejeti z opravičilom, da se želi posvetiti znanosti. “Največja usluga, ki mi jo lahko narediš,” je rekel, “je, da mi omogočiš odmaknjeno življenje v senci tvojega bogastva. Tako bom lahko širil spoznanja znanosti in molil za tvoje dolgo življenje in blagostanje.” Modri vezir je sprejel opravičilo in mu radodarno dodelil 1200 miskalov zlata iz državne blagajne kot letno podporo. S tem se je lahko Hajam brezskrbno posvetil znanstvenemu raziskovanju na področju astronomije in matematike.
Njegov prijatelj as-Sabbah je to odločitev komaj dočakal in je zahteval mesto v vladi. Sultan je vezirjevo prošnjo odobril in as-Sabbah je dobil mesto na dvoru. S časom je postal nezadovoljen, padel je v razne dvorne spletke, v kratkem času je sestavil svojo stranko in neuspešno poskušal izriniti in odstraniti Nizamul al-Mulka. Ko so zaroto odkrili, se je moral umakniti Nizamul al-Mulkovi oblasti. Skril se je v Egipt pod okrilje Fatimidov, ki so bili seldžuški sovražniki. Kot učen človek in vratolomen duh je po mnogih nezgodah in potovanjih kmalu dosegel naklonjenost in zaupanje fatimidskega vladarja, ki ga je poslal v Sirijo širit ismaelitsko vero. Tu je v zelo kratkem čas našel mnogo pristašev v najnižjih slojih prebivalstva. Nekega dne je izmed najzvestejših privržencev organiziral anarhistično skupino asasinov. Postal je njihov vodja, njihov velik učitelj da’i al-du’ah. Skupini je bila sveta dolžnost slepo pokoravanje njemu kot šejku, njegovim naslednikom in izvrševanje ukazov brez ugovora. Skupina fanatikov je bila dolgo neznana in je zrasla v močno in nevarno organizacijo pod vodstvom as-Sabbahove močne in hudobne volje. Leta 1090 je zgradil grad trdnjavo Alamut, v bližini Kazvina v pokrajini Rudbar, ki leži na visokogorskem področju južno od Kaspijskega morja. Iz tega gorskega doma je kot nekdanji Hajamov prijatelj širil svojo zlobno slavo med križarji z imenom Šejhul-Džebel, Starec s planine, in sejal nasilje v mohamedanski svet. Postal je strah in trepet vsem dostojanstvenikom prednje in srednje Azije. Dolgo so razpravljali, ali beseda Assasin, ki so jo križarji prinesli v Evropo kot njihov temni spomin, izhaja iz besede hašiš (hashish – mamila konopljinih listov (indijsko bhang), arabsko hashshashun (haššaši), uživalec hašiša), s katerim so sebe spravljali v blaznost, ali iz imena ustanovitelja te zloglasne sekte, ki smo ga spoznali v tihih tovariških dneh šolanja v Najšaburju. Zgodbo so kot izročilo nekaj časa označevali kot legendo, češ da je izmišljena.
 Ilustracija (avtor JM).
Ilustracija (avtor JM).
V svoji že omenjeni knjigi (po tedanjih običajih je Hajam dobil veliko nadimkov Zakladnica Modrosti, Čuvar ali Kralj Modrosti, Dokaz Resnice) ga je al-Bajhaki označil kot poznavalca jezika, muslimanskega prava in zgodovine. “Preden je odšel v Isfahan, je neko knjigo prebral sedemkrat, in se jo je tako naučil na pamet. Ko pa se je vrnil v Najšabur, jo je narekoval, tako da se besedilo ni mnogo razlikovalo od originala.” Po takšnem izrednem spominu sta bila znana tudi njegov pesniški predhodnik al-Ma’arri in prijatelj al-Gazali. Knjižnic zaradi tega dejansko skoraj niso potrebovali. Al-Bajhaki je imenoval Hajama Abu Alijevega naslednika v različnih filozofskih znanostih. Abu Ali je bil tadžikiški matematik, filozof in zdravnik Ibn Sina al-Husein ibn abd Allah (latinsko Avicena) (975-1037). Takrat so znanost delili na teoretično in praktično: teoretična je obsegala višjo znanost ali metafiziko (danes filozofija), srednjo znanost (astronomija in matematika) in nižjo znanost (fizika); praktične znanosti pa so bile politične, pravne ter moralne znanosti.
“On je modrec, človek, ki je vešč v vseh področjih filozofije, še posebno v matematiki.” Tako je pisal o Hajamu tudi arabski geograf in kozmograf Zakarij al-Kazvini (umrl 1283) v svojem kozmografskemu traktatu Spomeniki mest in poročila o božjih slugah (Athar). O njegovem življenju je pisal tudi arabski zgodovinar Ibn al-Qifti (1172-1248) v pomembnem delu Zgodovina modrih za znanstvenike (Ikhbar al-Ulama’ bi-Akhbar al-Hukama), ki ga poznamo po skrajšani izdaji. Po končanem študiju se je Hajam kot mnogo mladih znanstvenikov tedanjega časa znašel v revščini. Vladarji so sprejemali samo tiste, ki so jih v svojih pesmih na veliko hvalili ali pa tiste, ki so se hvalili, da znajo natančno določiti horoskop. Sam Hajam je o tem pisal v uvodu svojega prvega matematičnega traktata in potožil, da mu je bilo v mnogih letih onemogočeno ukvarjati se s svojim najljubšim delom, to je algebro. “Bili smo priče propada in zmanjšanja števila učenih ljudi. Samo nekaj jih je ostalo, mnogi so nesrečno končali.” Potem je govoril o takoimenovanih lažnih znanstvenikih, ki “resnico oblačijo z lažjo”: “Kruta usoda jih je, dokler žive, z medsebojno zaprisego napotila izboljševat in raziskovat znanost. Vendar večina njih, ki se danes izdajajo za učenjake, tajijo resnico z lažmi in ne presegajo okvirja pol-učenjaštva, saj svoje znanje postavljajo v službo z materialnimi in nizkimi cilji. Če srečate človeka, ki teži za resnico in ljubi iskrenost, zavrača pretvarjanje in laž, ki se izogiba slepilom, bo postal predmet preziranja in posmehovanja.”
Za Abu Tahirjem je bil njegov naslednji pokrovitelj buharski hakan Šams al-Muluk, po letu 1074 pa sam seldžuški sultan Dželaluddin (Veličanstvo vere) abu-al-Fath Malikšah, ki je 1071 nasledil svojega očeta sultana Alp Arslana. V tem času je Hajam izdelal novi koledar, ki je dobil ime po enem izmed vladarjevih imen Takwimi al ta’rikh al-Džalali doba. Ta “časovni račun”, kot je rekel že angleški zgodovinar Edward Gibbon (1737-1794), prekaša julijanski koledar in je enakovreden gregorijanskemu. Nekateri sodobni znanstveniki trdijo, kakor pravi F. Rosen, da je bolj natančen kot gregorijanski koledar, v kar se seveda ni težko prepričati.
Med bivanjem v Isfahanu in Bagdadu je bil kot svobodomiseln učenjak izpostavljen napadom ortodoksnih ulemov, teologov, muslimanskih verskih in posvetnih strokovnjakov. O Hajamovi bližini Malikšahu priča tudi naslednja pripoved al-Bajhakija: “Imam Omar je rekel mojemu očetu: “Nekoč sem bil ob sultanu Malikšahu, ko je k njemu prišel emirjev deček in nas imenitno postregel. Bil sem navdušen nad tem, kako lepo je stregel v tako mladih letih”. Sultan mi je tedaj rekel: “Ne navdušujte se … goloba nihče ne uči, kako se vrne domov, pa vseeno leti iz Meke v Bagdad…”
V tem času so nastala tudi njegova najpomembnejša matematična dela. V njih se je ukvarjal s problemi reševanja enačbe tretje stopnje. Za takratni svet je pravzaprav zgradil teorijo pozitivnih realnih števil. Njegovo teorijo razmerij je poleg trigonometrije prinesel v Evropo v 13. stoletju at-Tusi s svojo knjigo O popolnem štirikotniku (Kitabu aš-Šaklu-l-kita’). Hajamova Algebra tako predstavlja precejšen dosežek, ker vsebuje sistematično preučevanje kubičnih enačb na povsem nov način. Uporabljal je metodo, ki so jo uporabljali tudi grški matematiki, po kateri je določal korene teh enačb s presečišči dveh stožernic. Numeričnih rešitev ni imel in je razločeval – prav tako po grškem zgledu – med geometrijskimi in aritmetičnimi rešitvami. Aritmetične rešitve naj bi obstajale le, če so koreni pozitivni ulomki. Po tem se ta pristop povsem razlikuje od pristopa italijanskih matematikov iz 16. stoletja, ki so uporabljali čisto algebrajske metode, in zanimivo bi bilo videti, kam bi šel njegov razvoj v tej smeri, če bi imel več časa za to delo.
V poeziji se je proslavil s svojimi rubajami, štirivrstičnimi verzi, ki jih je okoli 600 izdal v pesniški zbirki Četrtinke (Rubajati). Vsebinsko so mistične, skeptične in otožne. V bistvu pa so filozofski izreki, naperjeni zoper verske dogme, pa tudi anakreontični, nemenjeni proslavljanju užitkov. Njegovi verzi so, čeprav po obsegu krajši od katerekoli perzijske pesmi in na hitro napisani, rezultat neminljivih čustev in misli. Predstavljajo najverjetneje delo in dogodke njegovega življenja. Nanj je stilsko močno vplival slepi sirski pesnik in filozof abu-al-Ala’ al-Ma’arri (973-1057).
Njegov zaščitnik Malikšah je imel z njegovimi nasprotniki veliko težav. Prepričevali so ga o Hajamovem brezboštvu in skušali proti njemu izzvati javno mnenje, da bi mu sodilo. Proti njemu so se dvignili tudi drugi učenjaki in teologi, ker je bil negativno razpoložen do religije. Da je v resnici dobro poznal Ku’ran, pripoveduje neka al-Bajhakijeva zgodba, ki se veže na čas, ko je bil sultanov vezir Šahib al-Islam, Nizamul al-Mulkov sorodnik. Govori o srečanju pravovernega in ortodoksnega imama al-Gazalija ter skeptika in nevernika Hajama. Beseda teče o tolmačenju nekega spornega mesta v Ku’ranu. Pokazalo se je, da je obvladal slovnico bolje od vseh navzočih. Vendar pa to ni preprečilo verskih oblasti, da ga ne bi obsodile. Moral se je javno opravičiti. Da bi utišal nasprotnike, se je odločil za težko potovanje in odšel na romarsko pot v Meko in Medino. Ta pot je zanj pomenila pobeg iz neugodnega položaja in nekajmesečno brezbrižno življenje. Drugače te odločitve nikakor ne moremo spraviti v sklad z njegovimi rubajati.
Ko se je vračal iz svetega mesta, je obiskal Bagdad in svoje somišljenike in nekdanje učence, ki so ga nagovarjali, da bi ostal pri njih, se ukvarjal s pedagoškim delom, vendar je to zavrnil. Kaj je bil resnični vzrok temu danes ne moremo vedeti. Prijatelji in učenci so mu po vzhodnem običaju podelili častni naziv Hudždžetul-Hakk, kar pomeni Dokaz Resnice. Ta naslov je Hajam v resnici zaslužil, ker se ni nikoli obotavljal povedati resnico, pa čeprav je bila grenka, ulemom in ljudskim masam. Ljubezen do resnice mu je prinesla prijatelje tudi med načelnimi nasprotniki. Med drugimi mu je postal prijatelj tudi perzijski teolog, filozof in mistik Abu Hamid Mohamed al-Gazali (1058-1111), ki so mu ortodoksni ulemi nadeli naziv Hudždžetul-Islam (Dokaz Islama). Velikokrat je zahajal v Hajamovo družbo, pa čeprav sta se v razumevanju religije in filozofije razhajala. Ohranilo se je nekaj rubajat, v katerih Hajam apostrofira religiozno zakrknjenost sodobnih učenjakov in verjetno se nekatere nanašajo prav na al-Gazalija, ki je napisal znano delo Uničenje filozofije (Tahafut al-falasifa).
S smrtjo Malikšaha leta 1092 je bilo konec Hajamovih astronomskih raziskovanj in njegovega bivanja v Isfahanu. Tega leta je nek as-Sabbahov fida’i, preoblečen v muslimanskega puščavnika, zabodel Nizamul al-Mulka pri Sahni, ko se je vračal iz Hamadana v Kermanšah. Med bojem za oblast po Malikšahovi smrti, ki je trajal četrt stoletja, se je Hajam umaknil v svoj rojstni kraj in se boril proti nesrečam tedanjega časa in pomanjkanju. V uvodu svoje Algebre je povedal veliko o svojem težkem položaju v tistih burnih časih, ko je propadala cvetoča seldžuška država v državljanskih vojnah in ko je zloglasni as-Sabbah s številnimi četami assasinov neovirano širil svoje demonsko poslanstvo in moril, kogar je hotel. Mogoče je v tem času tudi sam pomislil, da bi lahko fanatični ismaelit postal pozoren nanj in pripravil kakšnega zločinca, da ga ubije, čeprav se je umaknil v samoto in se zaprl sam vase. Družil se je samo še z nekaterimi prijatelji, med katerimi so omenjali Abdurrezaka, ki je pozneje postal minister na dvoru sultana Sandžara (umrl 1157). Poleg njih mu je, kot poroča Bodenstedt, bila zvesta prijateljica Muza, ki ji je v svetlih in temnih dnevih zaupal vse skrivnosti duha in srca v lepem in zvočnem jeziku, ki je v tistih časih najbolj cvetel in ki ga je mojstrsko obvladal. Njegovi verzi še danes veljajo kot vzor perzijske poezije. Al-Bajhaki je spet navedel, da je takrat pisal in predaval zelo malo. Šahrazuri je zapisal, da je bil njegov tedanji učitelj tudi al-Isfazari, ki je bil do učencev prijazen, Hajam pa je bil do njih zagrenjen zaradi stanja v vladajočih krogih.
Ko so se državljanske vojne pomirile, so zanj prišli boljši dnevi. Leta 1112 je bival v Balhu v gosteh pri emirju Abu Sadu. Dve leti kasneje je živel v Mervu pri vezirju Ibnul-Muzafferu, ki ga je zelo cenil kot človeka in kot vsestransko izobraženega učenjaka. Ves ta čas in pozneje je deloval tudi kot astrolog. Njegov učenec, pesnik Khwajah Arudi ad-din Abu Muhammed Ilyas ibn ben Yusuf as-Samarkandi an-Nizami (ok. 1090 – ok. 1175) je povedal, da je istega leta napovedal ugoden čas za vojni pohod nekega sultana.
Pri koncu svojega življenja ni bil prepričan, ali je bil na svoji življenjski poti uspešen s svojim bojem proti neznanju. Umrl je 17. decembra 1131, o njegovi smrti pa je pisal an-Nizami ob obisku njegove grobnice štiri leta pozneje: “Petstošestega leta (1112) sta bila hodža imam Hajam in hodža al-Isfazari na dvoru emirja Abu Sada v predelu mesta Balha, kjer so stanovali delavci. Z njimi sem bil v veseli družbi. Velikokrat sem se v vrtu pogovarjal s svojim učiteljem. Slišal sem, kako je Dokaz Resnice, Omar, rekel: “Moja grobnica bo stala na takšnem mestu, da bo vsako pomlad severni veter raztrosil cvetje nad njo.” To se mi je zdelo nemogoče, vendar sem vedel, da takšen človek ne govori brez osnove. Ko sem v tridesetem letu (1135) spet obiskal Najšabur, so minila štiri leta, odkar je ta velik človek skril svoj obraz pod pokrov krste in zapustil ta svet. Bil mi je učitelj. V petek sem odšel na njegov grob in vzel nekega človeka, da me je vodil. Odvedel me je na pokopališče Haira. Pogledal sem na levo in videl čisto na koncu zid, nad njim pa hruškino in marelično drevo (drevesi, ki cvetita v različnih razdobjih), kako prek zidu sipata svoje cvetove na grobnico, tako da se je v celoti skrila pod cvetjem. Tedaj sem se spomnil Hajamovih besed, ki sem jih slišal v Balhu, in zajokal, saj na Zemlji nisem našel človeka, ki bi mu bil enak.”
O njegovih zadnjih trenutkih je pripovedoval Šahrazuri: “Omar je preučeval Knjigo zdravljenja. To je metafizični testament Ibn Sine (Kitab aš šifa). Pri poglavju Ednina in množina (Bog in svet) je vstavil vanjo zlat zobotrebec kot znak, do kod je prišel. Po molitvi je povedal zadnje želje svojim gostiteljem. Ta dan ni ne jedel ne pil. Ko je končal večerno molitev, je pokleknil in spregovoril: “Bog, resnično sem se trudil, da te spoznam, kolikor mi je bilo mogoče. Oprosti mi! Moje spoznanje Tebe naj bo moj zagovor pri Tebi.” Ko je to spregovoril, se je razšel z dušo.”
Vse njegovo delo v celoti govori, da ta epski skeptik svojega življenja ni preživel zastonj. O Hajamu so mnenja sodobnikov in poznejših rodov različna. Eni v njem vidijo predstavnika resnice na Zemlji, drugi pa, kakor pravi nek sodobnik, “nesrečnega filozofa, brezbožca in materialista”. Tako eni kot drugi pa mu priznavajo vsestransko izobrazbo, saj je v resnici bil velik v poznavanju Kur’ana in izročila, v poznavanju arabske in perzijske poezije ter bogat vir na področju filozofije in naravoslovnih znanosti. Poleg vsega Hajam ni bil nagnjen k pisanju kot njegov predhodnik Ibn Sina ali al-Gazali. Napisal je še nekaj del, ki pa se niso ohranila in jih poznamo samo še po naslovih: iz astronomije in vremenoslovja Lewazimul-emkine, matematična Prikaz natančnosti indijskih metod o iskanju tretjega in četrtega korena, o draguljih Nizamul-hukm, pesmi Zbirka Kasid in metafizični Elwugud in El-kewnu wet-teklif.
Končajmo z njegovimi besedami: “Moje rojstvo ni dalo vesolju najmanjše koristi. Moja smrt ne bo vzela ničesar njegovemu neizmerju in ničesar njegovemu sijaju. Nihče mi nikoli ni mogel povedati, zakaj sem prišel, in nihče, zakaj bom odšel.” Bolj optimistično mu dodajmo: “What life has taught me, I would like to share with those who want to learn …” in še “Teach me, teach me Persian mu’addib”.
Hajamov koledar
Po letu 1074 je bil Hajamov pokrovitelj sam seldžuški sultan Dželaluddin (Veličanstvo vere) abu-al-Fath Malikšah, ki je leta 1071 nasledil svojega očeta sultana Alp Arslana. O tem je pisal perzijski zgodovinar Izz-al-Din Ibn al-Asir (1160 – 1234) v svoji ogromni knjigi Popolna knjiga o zgodovini (al-Kamil fi al-Ta’rikh), kjer je o letu hidžre 467 (leto 1074) zapisal: “V tem letu sta Nizamul al-Mulk in sultan Malikšah zbrala vse svoje najboljše astronome. Premestili so Nauruz (danes pomladišče, pri njih novo leto) v začetno točko Ovna, do tedaj pa je Nauruz prihajal v času, ko se je Sonce nahajalo v sredini Rib, in pojavil se je koledar, narejen za sultana. Za sultana Malikšaha so zgradili observatorij. Pri gradnji so sodelovali najboljši astronomi, Abulhatim Muzafar al-Isfazari, Majmun Ibn Nadžib al-Basiti in drugi. Pri tem so porabili veliko denarja.”
V Mervu je Hajam tako na vezirjevo pobudo sestavil komisijo, ki bi spremenila obstoječi koledar. Skupaj s sedmimi astronomi je rešil to težko nalogo. Observatorij so zgradili v Isfahanu, čeprav nekateri navajajo, da so ga zgradili v Najšaburju, v Raiju, kjer je bil tedaj sedež vlade, ali celo v Bagdadu, kjer pa je že od leta 829 deloval še od časa abasidskega kalifa Abdulah al-Mamuna (813-833). Hajama so zaradi njegovih zaslug imenovali za direktorja tega velikega observatorija, kjer je pozneje izdelal Malikšahove astronomske tabele Ziji-Malik-šahi. Sam sultan je bil verjetno nepismen kot njegov oče in stric, Nizamul al-Mulk pa je bil kot Hajam med najbolj učenimi ljudmi. Zapustil je mnogo zgradb in dejanj, o katerih govori precej zgodovinskih zapisov, najbolj znan pa je zaradi svojega državniškega dela in reforme šolstva.
 Observatorij v Isfahanu – rekonstrukcija (avtor JM).
Observatorij v Isfahanu – rekonstrukcija (avtor JM).
Novi koledar je dobil ime po enem izmed vladarjevih imen Takwimi al ta’rikh al-Džalali doba. Ta “časovni račun”, kot je rekel že angleški zgodovinar Edward Gibbon (1737 – 1794), prekaša julijanski koledar in je enakovreden gregorijanskemu. Nekateri sodobni znanstveniki trdijo, da je bolj natančen kot gregorijanski koledar, v kar se seveda ni težko prepričati. Hajam se je skliceval na svojo reformo starega perzijskega muslimanskega lunarnega koledarja, ki ima napako enega dneva v 5000 letih (v 1540 ali 3770 letih po različnih razlagah, odvisno pač od vrednosti vzorčne dolžine tropskega leta), medtem ko se v našem gregorijanskem koledarju pojavlja napaka enega dneva vsakih 3330 let glede na dolžino tropskega leta ob uvedbi samega koledarja. Hajamov koledar je popravek julijanskega koledarja, ki ima mnogo astronomskih opravičil.
Pri sestavljanju takšnega solarnega koledarja se pojavi naslednja zanimiva naloga. Srednje tropsko leto traja zaokroženo 365,2422 dni, navadno meščansko leto 365 dni, prestopno meščansko leto pa 366 dni. Poiskati moramo čim manjši naravni števili x in y, tako da bo po preteku x navadnih in y prestopnih meščanskih let minilo x+y srednjih tropskih let. Torej morata x in y ustrezati pogoju:
kar daje:
Ker sta 1211 in 5000 tuji števili, sta najmanjši naravni števili, ki rešita zgornjo enačbo, x=3789 in y=1211. Med 5000 leti mora torej biti 3789 navadnih in 1211 prestopnih let. Dobljena rešitev zaradi velikih vrednosti ni preveč primerna za uporabo. Manjše približne rešitve zgornje enačbe v naravnih številih dobimo z verižnimi ulomki. Razvoj nam daje tabelo:
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| an | 0 | 4 | 7 | 1 | 3 | 4 | 1 | 1 | 1 | 2 |
| yn | 0 | 1 | 7 | 8 | 31 | 132 | 163 | 295 | 458 | 1211 |
| xn+yn | 1 | 4 | 29 | 33 | 128 | 545 | 673 | 1218 | 1891 | 5000 |
Prva približna rešitev v naravnih številih je torej x1+ y1 = 4, y1 = 1; na vsaka štiri leta pride eno prestopno leto. Tako je narejen julijanski koledar, ko je namesto 0,2422 vzet približek 0,25=1/4. Podobno lahko naredimo koledarje za vsakega od nadaljnjih približkov v tabeli. Ko namesto x, y postavimo približka xn, yn iz tabele, se vrednosti na levi in desni strani enačbe nekoliko razlikujeta. V gregorijanskem koledarju je namesto 0,2422 vzet približek 0,2425=97/400. Gregorijansko leto traja torej 365,2425 dni. Hajam je po tej enačbi vzel tretji približek, ki se je dobro skladal z dolžino tedanjega izmerjenega tropskega leta. Meritvam so na observatoriju posvetili veliko časa in pri tem uporabljali tudi drage inštrumente iz observatorija v Bagdadu, ker drugače tej nalogi ne bi bili več kos. Enostavno lahko vidimo, zakaj je njegov koledar boljši tudi od gregorijanskega, saj velja:
ali
Naslednji približek po spodnji tabeli – 31/128 – je leta 1863 v svojem koledarju predlagal nemški astronom Johann Heinrich Maedler (1794-1874), ki ima sicer boljšo sistematsko napako kot Hajamov koledar, vendar je skupna napaka zaradi prevelike periodične napake večja. Njegov predlog se ni obnesel.
Zanimivo je, da bo v 47. stoletju točen tisti koledar, ki bo upošteval že drugi približek 7/29, saj se bo tropsko leto za toliko skrajšalo. Trajanje koledarskega leta v Hajamovem koledarju je tako 365+8/33 dneva. Interkalacijsko pravilo je: v 33-letnem ciklu so prestopna leta tista, ki so deljiva s štiri, torej osem prestopnih let: četrto, osmo, dvanajsto, šestnajsto, dvajseto, štiriindvajseto, osemindvajseto in triintrideseto. To pomeni, da je sedemkrat prestopno četrto leto, osmič pa je prestopno peto leto. To pravilo predstavlja ne samo za tisti čas, ampak tudi za današnji, pravi znanstveni dosežek, čeprav je približek več kot enostaven. Drugi koledarji popravljajo sistematsko napako po 128, 400, 2000, 3200, 3600 ali 4000 letih, njegov koledar pa jo popravlja že po 33-ih letih. Zato je prednost te koledarske rešitve poleg drugih v tem, da ne čakamo napake celega dne in jo popravimo, ampak jo popravimo takoj, ko se poveča do četrtine dneva. Namesto 32. leta je prestopno 33. leto. Zato je periodična napaka izredno majhna – 1,2121 dneva. Takšno pravilo je tako enostavno, da ga je res težko izboljšati, če bi hoteli zmanjšati periodično napako. Periodično napako lahko, kot vse kaže, zmanjšamo samo pri še enakomernejši razporeditvi prestopnih let. Razpored dnevov po mesecih je zelo zanimiv:
31 31 31 31 31 31 30 30 30 30 30 29(30)
Po njegovem koledarju se novo leto začne prvega dne pomladi. Devet stoletij se je to vedno dogajalo. Takšen razpored dnevov po mesecih ni slučajen; od spomladnega do jesenskega enakonočja je Te = 186 dni 10 ur, od jesenskega do naslednjega spomladanskega enakonočja pa Tw = 178 dni 20 ur kot v njegovem koledarju. To je vedel in vgradil v svoj koledar pet stoletij pred Keplerjem. Upošteval je, da se Sonce približno sedem dni več nahaja na severni nebesni polobli kot pa na južni. Zato je prav neverjetno, da sestavljalci gregorijanskega koledarja niso vedeli za ta koledar, ki so ga že pet stoletij uspešno uporabljali. Težko je pojasniti, zakaj leta 1582 niso namesto gregorijanskega koledarja sprejeli Hajamovega koledarja. Pač pa so njegovo reformo vpeljali leta 1079 v Perziji, a ga je kasneje spet zamenjal muslimanski lunarni koledar z ero, imenovano hidžra, po Mohamedovi selitvi (arabsko higret) v petek, 16. (15.) julija 622 zaradi verskih nesporazumov iz Meke v Jesrib, pozneje Medina. Tja naj bi prispel 20. septembra 622. Hidžra temelji na luninem letu z dolžino 354,3666667… dni = 354 dni 8 ur 48 minut, ki je 6 sekund krajše od tedanjega astronomskega luninega leta in ima cikel 360 mesecev z 10.631 dnevi. Interkalacijsko pravilo je:
ali enostavneje:
To pomeni, da ima cikel 30 let z 12 meseci, ki imajo po vrsti izmenično 30 in 29 dni, s tem, da ima zadnji mesec v navadnem meščanskem luninem letu z dolžino 354 dni 29 dni, v prestopnem luninem letu z dolžino 355 dni pa 30 dni. V tem ciklu je 11 let, ki imajo zadnje tri mesece po 30 dni na koncu naslednjih prestopnih let:
19 let pa je navadnih meščanskih luninih let. Zaradi tega je periodična napaka prevelika: 2,2722 dneva.
Hajamov koledar so poleg hidžre uporabljali v Iranu vse do leta 1954. Bil je točen pred 38. stoletji. Od takrat se ni nabrala sistematska napaka niti za en dan in znaša: 4,19, in je manjša kot pri gregorijanskem koledarju: 4,92. Pri gregorijanskem koledarju je razmik med prestopnimi dnevi običajno 48 mesecev, včasih pa 96. Periodična napaka je še večja: 2,4400 dneva. Dodati moramo še sistematsko napako, ki je večja kot pri Hajamovemu koledarju. V Hajamovem koledarju je ta razmik sedemkrat 48 mesecev, osmič pa je 60. Zato je periodična napaka manjša. Razpored dnevov v letu v njegovem koledarju bi lahko bil tudi:
kar je boljša rešitev samo z dvema dolžinama mesecev. Pred sto leti je nastal predlog o enakomernejši razporeditvi dnevov v letu. Po tem predlogu imajo tromesečja 91 dni (po mesecih: 31, 30 in 30), en dan bi bil izven mesecev kot novo leto, v prestopnih letih bi dodali prestopni dan v sredini leta 31. junija. Leto v tem predlogu bi imelo razporeditev dnevov:
kar je prednost glede na gregorijanski koledar, ker imajo meseci samo dve dolžini. Nekateri avtorji takšen znan predlog napačno imenujejo koledar. Koledar ima razporeditev dnevov po mesecih v navadnih in prestopnih letih in hkrati tudi interkalacijsko pravilo, saj se mora vedeti, katera leta so prestopna. Če zadržimo interkalacijsko pravilo gregorijanskega koledarja, se bo tudi pri boljšem razporedu dnevov v letu v okviru cikla 400 let pomlad začenjala na tri različne datume. Pri Hajamovem koledarju nastopa pomlad v dveh datumih, in to pogosteje na (njegovo) novo leto, ker je njegovo interkalacijsko pravilo bližje naravnemu dogajanju. Popravek njegovega koledarja glede na periodično napako je sicer točnejši, nikakor pa ni enostavnejši. Takšen spremenjen koledar bi imel prav tako 33-letni cikel z osmimi prestopnimi leti, ki so deljiva s štiri, in dve dolžini mesecev. Nekatera leta bi imela tako razpored po mesecih:
kjer + označuje, da ima ta mesec lahko en dan več v prestopnem letu. V četrtem letu cikla je to 31. februar, v osmem letu cikla 31. marec, …, v dvaintridesetem letu cikla je to 31. december. Tako bi dosegli, da je razmik med prestopnimi dnevi izmenoma 50 in 49 mesecev. Zaradi tega se periodična napaka zmanjša na 1,0101 dni, sistematska napaka pa ostane enaka kot pri izvornem Hajamovem koledarju. Takšen koledar ima manjšo periodično napako in samo dve dolžini mesecev, vendar je bolj zapleten. Idealni solarni koledar ima periodično napako natanko en dan, a je prezahteven, ker pri tem prestopni dan nastopi, ko se nabere enodnevna napaka, tako da se verjetno nikoli ne bo uporabljal. Vse naslednje poprave Sončevih koledarjev morajo upoštevati ta Hajamov doprinos. V prvih sto letih naše dobe ima od njegovega koledarja manjšo sistematsko napako “koledar 62” – 1,18 dni, katerega cikel sestavljata dva Hajamova cikla, zmanjšana za en julijanski cikel z dolžino leta 365 + 15/62. Pri takšnem koledarju bi lahko vzeli enako razporeditev prestopnih dni kot v zgornjem primeru, vendar bi tudi tako ostala enostavnost Hajamovega koledarja neprekosljiva. Njegov koledar je tako še vedno najbolj natančen solarni koledar glede na periodično napako in enostavnost. Najboljši lunarni koledar glede na sistematsko napako pa je izdelal Hiparh.
Marca 1976 je iranski parlament uvedel novo dobo, ki se začenja 558 pr. n. š. in se ravna še naprej po starem iranskem muslimanskem lunarnem koledarju. Leto 2000 bo po tem koledarju že leto 2559.
V tem času dela na observatoriju so nastala tudi njegova najpomembnejša matematična dela. V njih se je ukvarjal s problemi reševanja enačbe tretje stopnje. Njegova Razprava o dokazih nalog algebre in almukabale predstavlja poleg zbornikov, ki so bili običajni v tistih časih, zelo izviren doprinos k razvoju teorije enačb tretje stopnje. V uvodu je Hajam zapisal: “Umetnost algebre in almukabale je, očitno, znanstvena sposobnost, katere predmet predstavlja absolutno število in izmerljive količine, ki se pojavljajo kot neznanke v odnosu proti katerikoli znani količini ali odnosu…” Nadalje je zapisal: “Algebrajsko reševanje se izvaja s pomočjo enačb, to je, kot je dobro poznano, z dodajanjem stopenj.”
Pri njem je prvič dozorela domneva, da so razmerja pravzaprav števila. Takole je zapisal: “Izberimo enoto in vzemimo njeno razmerje do količine G, kakršno je razmerje A k B. Na G ne glejmo kot na črto, ploskev, telo ali čas, v njej vidimo raje količino, ki jo je razum odmislil od vsega tega, količino, ki sodi med števila, seveda ne med absolutna in prava, saj se rado zgodi, da razmerje A k B ni številsko, se pravi, da ni dveh števil, ki bi bili v tem razmerju.” Števila, absolutna in prava so naravna števila. Hajam je torej za razmerji zaslutil razširitev pojma števila. Za takratni svet je pravzaprav zgradil teorijo pozitivnih realnih števil.
Navedel je glavne tipe kubičnih enačb, ki jih je razdelil v štiri velike skupine in za vsak tip posebej izdelal grafično metodo, ki je privedla do rešitve. Francozi so pozneje ponatisnili in prevedli to njegovo arabsko razpravo o algebri.
S smrtjo Malikšaha leta 1092 je bilo konec Hajamovih astronomskih raziskovanj in njegovega bivanja v Isfahanu. O teh težkih časih in zadnjih dnevih observatorija je pisal tudi Ibn al-Asir: “Observatorij je deloval do sultanove smrti, do leta štiristopetinosemdeset (leto 1092). Nato so ga zaprli.” Da bi svoje seldžuške gospodarje pripravil k temu, da bi prispevali denar za nadaljevanje dela na observatoriju, je Hajam napisal delo Nuruz-name, ki se ukvarja z legendami stare Perzije. Delo pa ni zadovoljilo Malikšahove vdove Taurkan-hatun, ki ni bila naklonjena ne Hajamu ne znanosti. Dosegel ni nič. Poleg samovoljne Malikšahove naslednice je bilo zaradi nasilja as-Sabbahovih ismaelitov samo delo v observatoriju v veliki nevarnosti, tako da na žalost koledarja ni mogel do konca dolgoročno preveriti in ga ni nikoli niti do konca dokončal. Tudi svoj Naravoslovni priročnik je posvetil sinu vezirja Muajida al-Mulka, kjer je zapisal: “Ko sem stopil v službo pravičnega gospoda Fahr al-Mulka, Muajidovega sina, me je obdaril s svojo milostjo. Potreboval je knjižico o vsesplošnih znanostih. Da sem ugodil tej prošnji, sem napisal to delo kot razpravo.” Končajmo s Hajamovimi besedami. Leta 1077 je končal svoj drugi matematični traktat Komentarji o nekaterih problemih k Evklidovemu delu, kjer je na koncu zapisal na običajen način za tiste čase: “Zaključek črnitve te beline se je zgodil v mestu (…) v tamkajšnji knjižnici, na koncu džumada al-ula štiristo sedemdesetega leta (v sredini decembra 1077).”
Jani Melik, ponatis članka iz revije Spika (september 1994)