Aristarhova metoda merjenja razdalje do Sonca in Lune
Aristarh je živel v Aleksandriji okoli leta 270 pr.n.š. in je prvi za katerega vemo, da je poskušal meriti razdalje v vesolju. Njegovo edino ohranjeno delo nosi naslov O razdalji med Soncem in Luno. Poglejmo si, kako se je lotil merjenja te razdalje:
Najprej je izmeril zorni kot Sonca oziroma Lune, saj sta približno enaka.
| 2RS
2RL |
= | D
d |
d | = | 2RS
D |
Nato je v dihotomiji (to je trenutek, ko je Luna natanko do polovice osvetljena) izmeril kot, ki ga oklepata Luna in Sonce.
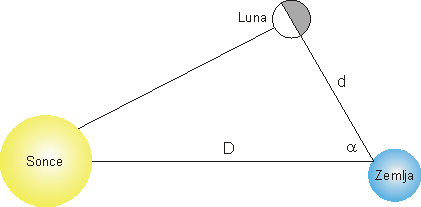
| cosa | = | d
D |
Nazadnje pa je izmeril še čas, ki ga Luna potrebuje, da med Luninim mrkom cela vstopi v Zemljino senco, ter čas, ki ga prebije v njej. Iz tega je lahko izračunal, koliko Luninih polmerov je široka Zemljina senca na razdalji, kjer vanjo vstopi Luna, kar je enako kot razdalja med Zemljo in Luno:
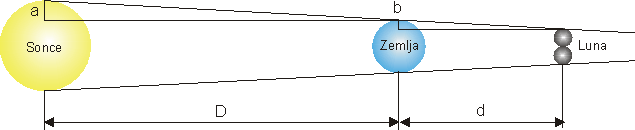
| b
a |
= | RZ – 2RL
RS – RZ |
= | d
D |
Zbrane meritve so zadostovale, da je lahko izrazil polmer Sonca in Lune ter njuno razdaljo od Zemlje s pomočjo Zemljinega polmera:
RL = RZ / 22 RS = 312 RZ d = 81 RZ D = 1550 RZ
Njegove meritve se sicer ne ujemajo preveč natančno z današnjimi (največjo mersko napako je storil pri merjenju kota med Luno in Soncem, ko je Luna osvetljena do polovice), a so le pomenile bistven napredek v zgodovini astronomije.
Sodobne metode merjenja razdalj v vesolju
Današnja tehnika merjenja razdalj do planetov, zvezd in galaksij temelji na verigi medsebojno pogojenih metod, katerih osnova je natančno poznavanje povprečne razdalje med Zemljo in Soncem oz. med telesi v našem sončnem sistemu. Ker so metode za merjenje večjih razdalj odvisne od natančno izmerjenih krajših razdalj, se vsaka napaka v verigi medsebojno pogojenih meritev pozna pri vseh meritvah od tega člena verige naprej. Kljub temu pa astronomom vseeno uspeva, da izmerijo razdalje tudi do najbolj oddaljenih galaksij že do nekaj deset odstotkov natančno.
Radarske meritve
Prvi člen v verigi metod za merjenje astronomskih razdalj so radarska merjenja razdalj med planeti v našem sončnem sistemu. Z radarsko anteno, ki jo usmerijo z Zemlje proti kateremu od bližnjih planetov, odpošljejo zelo močan pulz radijskih valov, pri čemer natančno izmerijo čas, ki preteče od trenutka oddaje pulza, do trenutka, ko radar zazna odmev s planeta. Ker potujejo valovi s konstantno svetlobno hitrostjo, lahko po tej metodi zelo natančno izmerijo razdaljo med telesi osončja.
Paralaksa
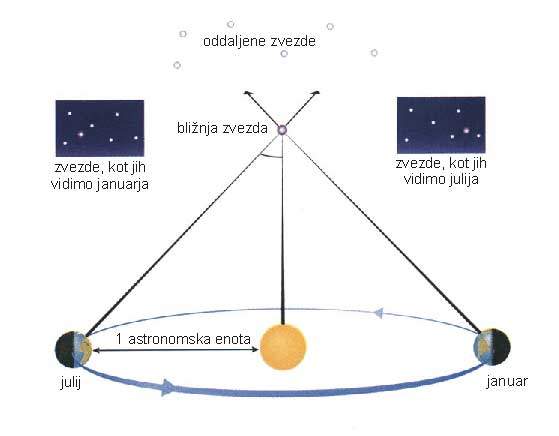
Druga stopnja v verigi so meritve razdalj do bližnjih zvezd s pomočjo paralakse. Poskusimo jo razumeti preko preprostega poskusa. Zapri eno oko in predse stegni roko z dvignjenim palcem tako, da prst zakrije nek oddaljen predmet. Sedaj na hitro zamiži na drugo oko in palec se bo, glede na ozadje, čudežno premaknil. Seveda ni takšen premik nič nenavadnega, če le poznamo osnove geometrije. Pri astonomskih meritvah naši očesi iz poskusa s palcem predstavlja Zemlja, palec pa je bližnja zvezda, katere razdaljo merimo. Preprosto izmerimo navidezni premik bližnja zvezda v primerjavi z oddaljenimo zvezdami, ko se Zemlja zavrti za polovico kroga okoli Sonca (v pol leta). Ko poznamo kot, za katerega se premakne zvezda v pol leta, lahko s trigonometričnimi formulami izrazimo razdaljo do zvezde z razdaljo med Zemljo in Soncem, katere povprečna vrednost se imenuje tudi astronomska enota.
Standardni svetilniki
S pomočjo paralakse lahko merimo razdalje do nekaj sto svetlobnih let daleč, pri bolj oddaljenih objektih pa postanejo zadeve bolj zapletene. V vsakdanjem življenju smo navajeni, da ocenjujemo razdalje s primerjavo velikosti objektov, ki so nam domači in katerih velikost je približno enaka. Če vidimo hišo na sosednjem griču, ki je navidezno za petkrat manjša od hiše, ki stoji 100 m od nas, seveda sklepamo, da je sosednji grič oddaljen 500 m. Vendar lahko takšne primerjave med velikostjo objektov v vesolju pripeljejo do velikih zmot. Galaksije so npr. zelo različnih velikosti, same zvezde pa so večinoma premajhne, da bi videli kaj drugega kot zgolj točko. Astronomi zato raje določajo razdalje s primerjavami svetlosti oddaljenih objektov. Preprosta formula namreč povezuje navidezno svetlost objekta z njegovo svetilnostjo in razdaljo s katere ga opazujemo:
| navidezna svetlost | = | svetilnost
4 |
Navidezno svetlost lahko izmerimo z inštrumenti na Zemlji, tako da lahko za objekt, katerega razdaljo poznano, izračunamo tudi izsev. Recimo, da vidimo oddaljeno cestno svetilko in vemo, da vse svetilke te vrste svetijo z močjo 1000 W. Če nato z detektorjem izmerimo navidezno svetlost te svetilke (v enotah W/m2), lahko po zgornji formuli izračunamo razdaljo.
Predmetu, kakršen je cestna svetilka, za katerega poznamo izsev, pravimo standardni svetilnik. Težava pa je, da podatka o izsevu za astronomske objekte na žalost ne moremo najti kar v katalogu, ampak ga moramo nekako drugače ugotoviti. Ena od možnosti je, da po vesolju iščemo zvezde, ki so zelo podobne našemu Soncu in katerega svetilnost poznamo (3,8 * 1026 W). Vendar takšne meritve niso zelo zanesljive, saj nikoli ne moremo biti povsem prepričani, da je svetlost oddaljene zvezde res tako zelo podobna Sončevi.
Meritve s prilagajanjem glavni veji H-R diagrama
Seveda pa postanejo zvezde, ki sevajo kot naše Sonce, na razdaljah večjih kot 1000 svetlobnih let premalo svetle, da bi jih lahko dobro opazovali. Opreti se moramo na bolj svetle zvezde, vendar izseva teh še ne poznamo.
Različne tipe zvezd lahko primerjamo z različnimi vrstami žarnic. Kot vsi vemo, se žarnice med seboj razlikujejo po moči (koliko wattov ima katera) in po barvi (nekatere so rumene, druge bele, tretje modrikaste…). Podobno je tudi pri zvezdah, le da te razlikujemo po izsevu, kar je enako kot moč pri žarnicah, in po spektru, kar pri analogiji z žarnicami ustreza barvi. Sedaj si zamislimo, da imamo spisek podatkov o vseh žarnicah, ki jih proizvajajo po svetu. Za vsak tip imamo dva podatka: moč in pa barvo. Podatke vnesemo v shemo in tako dobimo grafični pregled nad tem, katere kombinacije barv in moči so na voljo. Za zvezde sta takšno shemo naredila neodvisno en od drugega Ejnar Hertzsprung in Hery Norris Russell in se po njima imenuje H-R diagram. Na eni osi sta nanašala spektralne lastnosti, ki so pri zvezdah zelo odvisne od temperature na površini zvezde, na drugo os pa izsev, ki po naši analogiji ustreza moči žarnice. Ugotovila sta, da večina zvezd (to so zvezde, katerih gorivo je vodik) leži na glavni veji diagrama, ki približno ustreza pravilu, da je svetilnost zvezde večji, če je temperatura na površini zvezde večja. Le nekaj neobičajnih zvezd, kot so bele pritlikavke in pa orjakinje, leži izven glavne veje diagrama.
Večkrat se zgodi, da so zvezde zbrane v gručo in takšne objekte imenujemo zvezdne kopice. Predstavljamo si jih lahko kot roje zvezd. Za astronome so zelo zanimive in uporabne predvsem iz dveh razlogov: vse zvezde v kopici so približno enako oddaljene od Zemlje in vse zvezde v kopici so nastale približno v istem času, z zamikom mogoče nekaj milijonov let. Preko teh dveh skupnih lastnosti zvezd v kopicah, lahko astronomi z nekaj triki izmerijo razdaljo do teh zvezd in njihovo starost. Poglejmo, kako metoda deluje v praksi:
- Najprej morajo odkriti kopico, ki je dovolj blizu, da lahko njeno razdaljo določijo s pomočjo paralakse. Nato to kopico skrbno preučijo in izrišejo njen H-R diagram. Ker poznajo razdaljo do teh zvezd, lahko iz njihove navidezne svetlosti izračunamo njihove izseve, tako da izdelava H-R diagrama ni težavna.
- Nato izmerijo navidezne svetlosti zvez v zvezdni kopici, ki je predaleč, da bi razdaljo do nje lahko ugotovili s pomočjo paralakse. Če sklepajo, da imajo zvezde na glavni veji v oddaljeni kopici enake izseve, kot zvezde v nam bližnji kopici, lahko po zgoraj opisani formuli izračunajo razdaljo do oddaljene kopice.
Kefeide
S pomočjo zgornje metode lahko dobro merimo razdalje znotraj naše galaksije, za merjenje razdalj do sosednjih galaksij pa ni več uporabna, saj je večina zvezd na glavni veji H-R diagrama preslabotnih, da bi jih lahko gledali tudi z najmočnejšimi teleskopi. Tu nam na pomoč priskočijo Kefeide, ki so zelo svetle zvezde, tako da jih lahko opazujemo tudi v sosednjih galaksijah, hkrati pa imajo še eno zelo uporabno lastnost. Njihova svetlost se s časom periodično spreminja, kar za nas izgleda, kot da bi utripale. Perioda enega utripa je sorazmerna njihovemu povprečnemu izsevu. To pomeni, da lahko iz podatka o dolžini ene periode utripanja, izračunamo povprečni svetilnost takšne zvezde.
Kefeide so igrale zelo pomembno vlogo pri odkritju, da naša Mlečna cesta ni edina galaksija v vesolju, ampak le ena od mnogih. Že v sredini 18. stoletja se je med astronomi razširila polemika, ali je Andromedina galaksija, ki jo lahko vidimo tudi s prostim očesom, le “spiralna nebula” znotraj naše galaksije, ali pa je leži daleč stran in je po velikosti podobna naši galaksiji. Spor je uspel razrešiti šele Edwin Hubble leta 1924, ko je s pomočjo novega teleskopa na gori Mont Wilson v Kaliforniji odkril Kefeide v Andromedini galaksiji tako, da je primerjal fotografije, ki jih je posnel v razmiku nekaj dni. Takrat še ni vedel, da sta pravzaprav dva različna tipa Kefeid, zato je bila njegova meritev razdalje do Andromede za polovico prekratka, a še zmeraj dovolj dobra, da je potrdil domnevo, da je Andromeda res galaksija, ki leži daleč stran in je podobna naši.
Hubblov zakon
Vendar Hubble ni bil zadovoljen le z meritvijo razdalje do ene galaksije, ampak se je lotil sistematičnega merjenja razdalj do čim več takrat poznanih galaksij in v nekaj letih je prišel do enega najbolj presenetljivih odkritij v zgodovini znanosti. Ugotovil je, da vesolje ni statično, ampak galaksije bežijo stran druga od druge.
Astronomi so že v začetku 20. stoletja spoznali, da je spekter svetlobe s “spiralnih nebul” premaknjen proti rdečemu delu. Značilne črte v spektru so bile premaknjene proti večjim valovnim dolžinam. Do tega pojava pride, če se predmet, ki svetlobo oddaja, od nas oddaljuje, vendar dokler Hubble ni dokazal, da so nebule pravzaprav oddaljene galaksije, nihče ni prav dobro vedel, kako te spremembe spektra pojasniti.
Leta 1929 je Hubble razglasil svojo ugotovitev: bolj kot je galaksija oddaljena, večji je njen rdeči premik in zato večja hitrost, s katero se od nas oddaljuje. Prva objava te ugotovitve je temeljila na zelo majhnem številu obravnavanih galaksij in tudi Hubblova metodologija ni bila povsem sprejemljiva, saj se je kasneje izkazalo, da je pri oddaljenih galaksijah vzel za standardne svetilnike kar cele jate zvezd, čeprav je mislil, da gleda zelo svetle posamezne zvezde. Vendar je imel srečo, kajti kasnejše bolj natančne meritve so potrdile njegovo domnevo, ki jo lahko izrazimo tudi z preprosto formulo, ki nosi njemu v čast ime Hubblov zakon:
v = H0 * d
v označuje hitrost oddaljevanja galaksije, d, razdaljo do galaksije, H0 pa Hubblovo konstanto, katere vrednost običajno izražamo v čudnih enotah kilometrov na sekundo na megaparsek (kma/s/Mpc).
Ko enkrat poznamo vrednost Hubblove konstante, lahko iz rdečega premika galaksije po Hubblovem zakonu določimo njeno oddaljenost po formuli d = v /H0 . Vendar smo tudi tukaj soočeni z nekaj težavami, saj imajo galaksije poleg hitrosti, ki jo obravnava Hubblov zakon tudi medsebojne relativne hitrosti, ki jih Hubblov zakon ne obravnava, predvsem pa smo pri tej metodi določanju razdalje omejeni z natančnostjo, do katere poznamo Hubblovo konstanto.
Supernove kot metoda za merjenje razdalj do oddaljenih galaksij
Proces merjenja H0 je kot proces kalibriranja skale. Tudi najboljši teleskopi na Zemljinem površju niso mogli najti Kefeid v galaksijah, ki so ležale daleč stran od naše lokalne jate galaksij, odkar pa deluje vesoljski Hubblov teleskop, pa lahko opazujejo Kefeide tudi v galaksijah, ki so oddaljene več deset milijonov svetlobnih let. S temi Kefeidami lahko umerimo standardne svetilnike, ki omogočajo merjenje še večjih razdalj, kot so npr. supernove.
Ko bele pritlikavke končajo svoj življenjski cikel, eksplodirajo v veličastni eksploziji, ki se jo vidi zelo daleč in ji rečemo, da se je pojavila supernova. Značilnost supernov, ki nastanejo ob eksploziji bele pritlikavke je, da so vse približno enako svetle, zato jih lahko uspešno uporabljamo kot standardne svetilnike. V sredini 1990-ih so se astronomi lotili velikega projekta iskanja supernov v oddaljenih galaksijah in s pomočjo globalnega in neprestanega spremljanja neba z vseh koncev sveta. Poleg tega, da so natančneje izmerili H0 so ugotovili tudi, (čeprav nekateri astronomi v njihove sklepe še dvomijo in čakajo na točnejše meritve) da se vesolje razteza vedno hitreje. Kako jim je to uspelo? Če bi merili, s kakšno hitrostjo se oddaljujejo galaksije danes, bi dobili natančno takšno napoved, kot jo predvideva Hubblov zakon. Ker pa potrebuje svetloba od oddaljenih galaksij do nas zelo veliko časa, so dobili z opazovanjem zelo oddaljenih galaksij informacijo tudi o tem, kako hitro se je vesolje napihovalo v preteklosti. Meritve kažejo na to, da se vesolje napihuje vedno hitreje, ker ima pomembne posledice tudi za debato, kateri model vesolja je pravi?
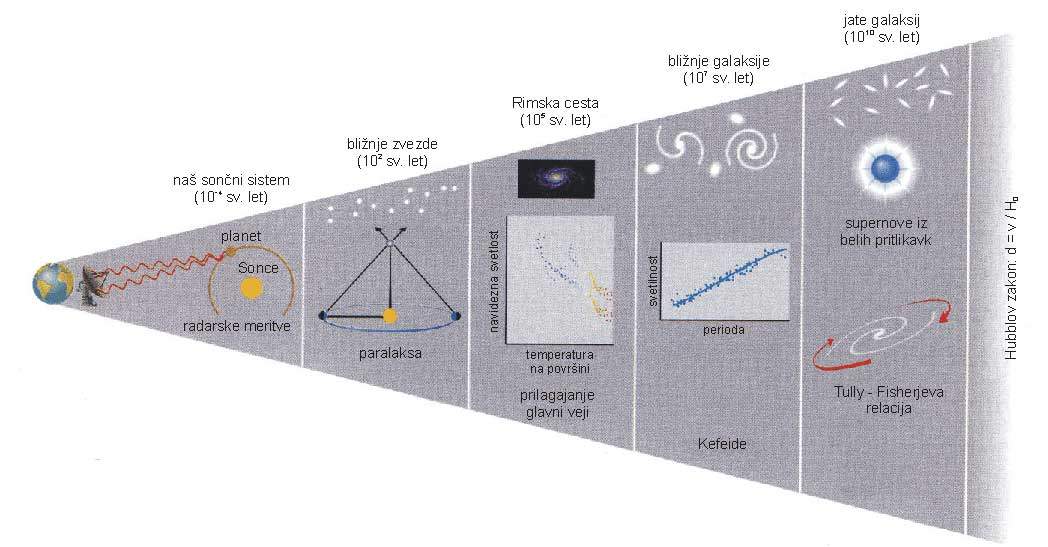
Povzetek verige za merjenje razdalj v vesolju:
- radarsko merjenje: Razdalje znotraj našega sončnega sistema merijo s pomočjo zakasnitve odmeva pulza radijskih valov, ki ga pošljejo do bližnjih planetov. Na ta način lahko zelo natančno določijo povprečno razdaljo Zemlje do Sonca
- paralaksa: Razdalje do bližnjih zvezd merijo s pomočjo spreminjanja lege bližnjih zvezd glede na bolj oddaljene, ko se Zemlja giblje okoli Sonca. Te meritve se naslanjajo na že prej izmerjeno razdaljo Zemlja – Sonce.
- prilagajanje zvezd glavne veje: S pomočjo paralakse so izmerili razdaljo do bližnje zvezdne kopice Hyades. S primerjavo zvezd z glavne veje v tej kopici z zvezdami v drugih kopicah znotraj naše galaksije, lahko izmerijo razdalje med posameznimi deli naše galaksije.
- Kefeide: S pomočjo Kefeid, ki se nahajajo v zvezdni kopici, ki smo ji že določili razdaljo, lahko umerimo tudi relacijo med periodo utripanja Kefeid in njihovo svetilnostjo. Ko odkrijemo Kefeido v oddaljeni galaksiji, lahko preko njene periode izračunamo njen svetilnost in tako razdajo.
- supernove, ki nastanejo iz belih pritlikavk (tip Ia): Ko enkrat poznamo razdalje do bližnjih galaksij, lahko z opazovanjem eksplozij supernov v njih določimo, kakšen je svetilnost imajo posamezne eksplozije in tako tudi razdaljo do vseh novih eksplozij.
- Hubblov zakon: Ko enkrat s pomočjo supernov in še nekaterih relacij (npr. Tully-Fisherjeva relacija, ki povezuje hitrost vrtenja galaksije z njeno svetilnostjo), lahko natančno določimo Hubblovo konstanto. Ko pa jo enkrat poznamo dovolj natančno, lahko razdalje do oddaljeni galaksij določamo kar preko rdečega premika.
kvarkadabra.net – številka 17 (december 2002)


















Hvala za ta članek!!!
To mi bo precej olajšalo raziskovalno nalogo. 😉