Keplerjev problem

Elipse so rešitve tako imenovanega Keplerjevega problema. Keplerjev problem  je vprašanje, kako se gibljeta dve telesi, med katerima deluje le gravitacijska sila.  Na poti do rešitve lahko najprej odmislimo skupno gibanje težišča. Ker ni zunanjih sil, se težišče namreč lahko le enakomerno giblje ali pa je na miru. Za gibanje okoli skupnega težišča nato obstajajo trije tipi rešitev.

1.  vezan sistem: to je tedaj, ko je kinetična energija sistema manjša od vezavne gravitacijske energije. Telesi se gibljeta po zaključenih tirnicah,  katerih najbolj splošna oblika je elipsa (tudi krog je elipsa in sicer z ekscentričnostjo enako nič).  Telesi se gibljeta tako, da sta vedno na nasprotnih straneh težišča, le to pa je v gorišču obeh elips. Ekscentričnost elipse  je definirana preko razmerja velikosti velike (a) in male (b) polosi elipse
   
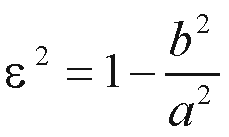
   Za krog, kjer je sta obe polosi enaki in je r=a=b, je torej ekscentričnost enaka nič. Ekscentričnost eliptične orbite v Keplerjevem problemu določa razmerje med energijo E, vrtilno količino L in masama teles, m₁, m₂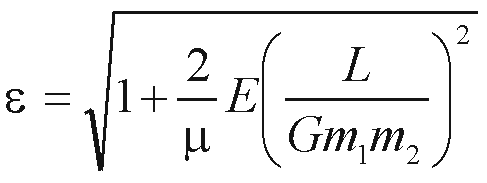
   
   kjer je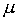 reducirana masa
   1/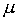=1/m₁+1/m₂

2. odprt sistem, telesi se gibljeta po parabolah; tedaj je skupna energija (vsota kinetične in potencialne) enaka nič

3. odprt sistem, pri čemer se telesi gibljeta po hiperbolah; to je tedaj, ko je kinetična energija večja od vezavne gravitacijske.

V primerih 2. in 3. sistem torej ni vezan in tirnice niso zaključene.

Še to, velikost elips po katerih se gibljeta planeta je obratno sorazmerna z maso posameznih teles. Težje telo od obeh se tako giblje bliže težišču kot lažje, pri čemer je razmerje velikosti elips (npr. njunih velikih polosi) kar m₁/m₂. Za sistem Sonce-Zemlja je razmerje mas že tolikšno, da je težišče sistema kar znotraj Sonca. Gorišču eliptične orbite, po kateri potuje Zemlja, torej leži znotraj Sonca (rečeno manj natančno, Sonce leži v gorišču elipse, ki jo opisuje Zemlja pri gibanju okoli Sonca).

Do gornjih rešitev je prišel Kepler s pomočjo astronomskih opazovanj, ki jih je opravil Tycho Brahe. Le ta je zelo natančno opazoval gibanje planetov, kot ga vidimo iz Zemlje. Iz teh podatkov je Kepler postavil tri po njem imenovane zakone
1. Krožnice po katerih se gibljejo planeti so elipse, pri čemer je Sonce v njihovem gorišču
2. Zveznica med planetom in Soncem v danem časovnem intervalu zajame lik, ki ima konstantno ploščino
3. Razmerje velike polosi a in obhodnega časa a³/T² je enako za vse planete.
Te zakone zlahka izpeljemo iz Newtonovih enačb za dve telesi, ki se medsebojno gravitacijsko privlačita. Pri tem pa je potrebno tudi upoštevati, da je eno od teles (Sonce) veliko masivnejše kot drugo.  Rešitev za sistem devetih planetov in Sonca je potem le približna, saj smo zanemarili medsebojne motnje planetov med seboj. Ker so tovrstne motnje zelo majhne, je taka obravnava upravičena.

Keplerjev problem je računsko prvi rešil Newton, kar je bil tudi glavni uspeh njegove teorije gravitacije. Iz osnovnih enačb je namreč lahko napovedal gibanje planetov. Problem je rešil grafično, saj je bil to tedaj ustaljeni način reševanja enačb, a zato zelo kompleksen. Danes zna rešiti Keplerjev problem z uporabo diferencialnih enačb vsak študent prvega letnika fizike.

Več o rešitvah lahko prebereš v knjigi
Goldstein, Poole, Safko, Classical Mechanics

Zanimive povezave:

Heliocentrizem in cerkev
Keplerjevi zakoni -animacije
Galileo Galilei – med mitom in resničnostjo
O življenju in delu Nikolaja Kopernika

(Jure Zupan)

-