Vprašanje je sicer nekoliko nerodno zastavljeno, skriva pa v sebi tudi nekaj soli. Zakaj nerodno? Ker sta pač masa in energija telesa tako tesno povezani. Energija gibajočega telesa je vsota kinetične energije in mirovne energije (E=mc2), tako da je skupna energija za telo, ki se giblje s hitrostjo v
. Ker je hitrost telesa odvisna od tega v katerem sistemu ga opazujemo (se sami gibljemo skupaj s telesom, se gibljemo v nasprotno smer…), je torej tudi energija telesa odvisna od opazovalnega sistema. Odvisno od tega v katerem sistemu bomo energijo telesu izmerili, bomo dobili zanjo različne rezultate – energija telesa je odvisna od opazovalčevega sistema!
Da bomo lahko razglabljali o energiji vesolja, si moramo tako najprej izbrati opazovalni sistem. Za lažjo predstavo za trenutek pozabimo, da je prostor tridimenzionalen ter si zamislimo vesolje, ki bi bilo dvodimenzionalno. Primer take dvodimenzionalne tvorbe je balon. Ko se vesolje širi, je to tako, kot bi napihovali balon. Če balon posujemo s prahom, se bodo delci prahu med seboj s časom oddaljevali (saj je premer balona vedno večji), kljub temu da se glede na površino balona ne premikajo. Naš opazovalni sistem izberimo sedaj tako, da se vsedemo na enega od prašnih delcev ter opazujemo okolico okoli sebe.
Sedaj moramo naš dogovor le še prenesti v pravo vesolje in s tem tridimenzionalen prostor. Izberemo sistem v katerem se bodo snovni delci, ki napolnjujejo vesolje (sedaj npr. zvezde, planeti…) v povprečju gibali tako kot se širi vesolje. Zelo natančno vzeto je to sistem mikrovalovnega sevanja ozadja, čisto zadovoljivo pa je vzeti kar sistem Zemlje, ki se glede na mikrovalovno sevanje ozadja giblje s hitrostjo okoli 600 km/s , kar je še vedno dovolj počasi v primeri s svetlobno hitrostjo.
Sedaj se lahko lotimo sestave vesolja. Vesolje lahko popišemo, vsaj v prvem približku, kot idealen plin, ki je homogeno in izotropno porazdeljen po prostoru. Homogeno tu pomeni, da je v vsaki točki prostora enaka sestava, izotropno pa pomeni, da ob pogledu v poljubno smer vidimo enako sliko. To seveda ne ustreza povsem realnosti, saj okoli nas opazimo izrazite nehomogene strukture v obliki Lune, Zemlje, Sonca, naše galaksije, je pa dovolj dober približek na kozmoloških razdaljah.
K energijski gostoti “plina” bodo prispevali tako snov, radiacija, kozmološka konstanta in celo ukrivljenost. Pri tem je priročno njihove prispevke izraziti v deležih kritične gostote. Kritična gostota energije je tista gostota, ki ob izmerjeni ekspanziji vesolja ustreza ravnemu vesolju brez kozmološke konstante. Kritična energijska gostota vesolja ustreza približno štirim protonom na kubični meter.
V vesolju tako sedaj najdemo kar precej snovi, snovna gostota doseže okoli 30% kritične gostote energije. Ob tem je vidne materije, torej tiste ki seva, le za okoli 0.3% do 1% kritične gostote, medtem ko preostanek sestavlja temna snov, to je snov, ki ne seva. Nasprotno je radiacije, to je energije v obliki elektromagnetnega sevanja, za manj kot 0.01% kritične gostote in je kot taka sedaj povsem zanemarljiva pri ekspanziji vesolja.
Ni pa bilo vedno tako. Energijska gostota snovi se namreč spreminja kot R-3, kjer je R karakteristična skala vesolja (v primeru zaprtega vesolja je v sorodu z njegovim obsegom), medtem ko se energijska gostota radiacije spreminja kot R-4. Tako spreminjanje zlahka razumemo: ker je snov v glavnem na miru, so hitrosti snovnih delcev precej manjše od svetlobne, večino snovne energije predstavlja zato mirovna masa delcev (spomnimo se E=mc<sup>2</sup>). Če zanemarimo jedrske interakcije se število delcev ohranja (število protonov, nevtronov in elektronov). Ker se vesolje širi, je enako število delcev porazdeljeno po vedno večjem volumnu (V~ R3), od tu torej R-3 spreminjanje energijske gostote snovi.
Pri radiaciji se poleg večanja volumna, v katerem se nahajajo fotoni, spreminja tudi valovna dolžina elektromagnetnega valovanja. Ker se vesolje širi, se valovni paketi (fotoni) vedno bolj raztegujejo, njihova karakteristična valovna dolžina se torej spreminja kot R, oz. njihova energija kot R-1. Skupaj se tako energijska gostota radiacije spreminja kot R-4.
Ker se energijska gostota snovi in radiacije različno spreminjata z velikostjo vesolja, je nekoč v preteklosti obstajal trenutek, ko sta bili obe gostoti enaki. Pred enakostjo snovi in radiacije je prevladovala radiacija, po tem pa snov, saj se energijska gostota radiacije hitreje zmanjšuje z velikostjo vesolja kot energijska gostota snovi. Do enakosti radiacije in snovi je prišlo nekako 70,000 let po prapoku, kar ustreza rdečemu premiku okoli 3900. Samo za primerjavo: od nas najbolj oddaljeni kvazar, ki so ga odkrili do sedaj, ima rdeči premik okoli 5.0 . In še ena časovna ločnica: snov je prenehala biti v termičnem stiku z radiacijo okoli 300,000 let po prapoku, ko so se elektroni in protoni združili v vodik (čas rekombinacije). Tedaj je vesolje tudi postalo prozorno.
Pozorni bralec je verjetno opazil, da se skupna energija radiacije in snovi pri razvoju vesolja nista ohranili! Radiacija gre pač kot R-4 , snov pa kot R-3, kar moramo množiti z volumnom vesolja (ta gre kot R3), da dobimo celotno energijo vesolja (če je to končno, drugače lahko govorimo le o skupni energiji v nekem delu vesolja). Razlog tiči v tem, da nismo upoštevali tudi energije, ki jo nosi gravitacijsko polje. Le ta je pravzaprav skrita v ukrivljenosti prostora, vendar pa zveza ni povsem preprosta. Izkaže se, da je bolje kot vpeljevati energijo gravitacijskega polja, kar računati v ukrivljenem prostoru, pri čemer običajno ohranitev energije nadomesti njena posplošitev (učeno: kovarianten odvod tenzorja energije in gibalne količine je enak nič). Se pa zato v primeru idealnega plina ohrani entropija (vročega) vesolja (oz. dela vesolja, če je le to neskončno), kar pomaga pri računih.
Morda le še zadnja pripomba: temperatura vesolja se je spreminjala skladno z njegovim širjenjem. Tako so zgodnji trenutki vesolja bolj vroči, starejše vesolje pa je vse bolj hladno. Temperatura vesolja pravzaprav govori o povprečni energiji, ki jo nosijo delci, ki sestavljajo vesolje. Ob dovolj velikih temperaturah so bile povprečne energije delcev večje od mirovne mase le teh – hitrost gibanja delcev je bila primerljiva s svetlobno hitrostjo, rečeno drugače: delci so bili relativnostni. Elektroni so bili relativnostni pred starostjo vesolja okoli ene sekunde, protoni pa pred starostjo vesolja okoli 10-6s. Pri časih zelo blizu prapoka so bili tako vsi delci, ki jih sedaj poznamo, relativnosti. Večino energije je predstavljala kinetična energija, medtem ko je bila energija zaradi mirovne mase povsem zanemarljiva. Delce lahko pri teh časih v zelo dobrem približku obravnavamo kot brezmasne – nosijo le energijo, nič mase. Za celoten spekter delcev standardnega modela to velja na primer za čase manjše kot 10-10s po prapoku. Seveda pa so lahko ob tako kratkih časih po prapoku poleg delcev standardnega modela sestavljali vesolje tudi kakšni drugi delci (kot jih na primer napovedujejo teorije poenotenja), tako da je delčna sestava in s tem celotno razmerje kinetična energija: mirovna masa tako mladega vesolja neznana.
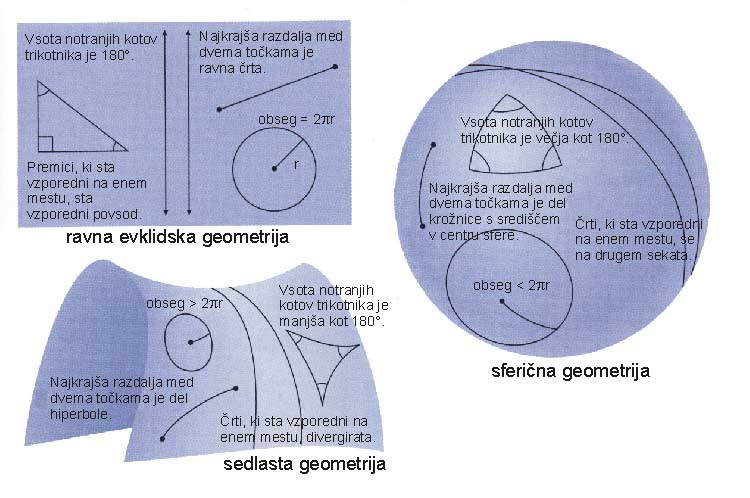
Dvodimenzionalno vesolje s konstantno pozitivno ukrivljenostjo je kar površina krogle, ki se s časom napihuje.
(Jure Zupan)
