Predavanje o veščini znanstvene imaginacije je imel harvardski profesor fizike in zgodovine znanosti Gerald Holton 14.2.1996 na zboru Ameriške akademije znanosti in umetnosti. V njem je predstavil tri orodja veščine znanstvene imaginacije: vizualno, analoško in tematsko imaginacijo. V prevodu smo izpustili Holtonov uvodni nagovor akademikom in dodali naslove poglavij.
Začetek moderne znanosti je tesno povezan z očesom kot organom vida. Marjorie Nicolson v svoji pionirski knjigi Znanost in imaginacija trdi, da bi “začetek moderne misli morda lahko postavili na noč 7. januarja 1610, ko je Galilei s pomočjo instrumenta (teleskopa), ki ga je razvil, mislil, da zaznava nove, razširjene svetove”. Galileijeve astronomske študije so klasičen primer, kako s potrpežljivim opazovanjem ustvariti nazorni vizualni miselni modela dogajanja, problem, ki je mučil veliko učenjakov: od Erwina Panofskega v petdestetih letih do Samuela Edgertona, I. Bernarda Cohena, Martina Kempa in drugih – sposojal si bom od vseh. Vendar je sposobnost vizualizacije fizikalnih pojavov pozneje sama doživela krizo.
Oko vidi tisto, kar hoče videti: prva opazovanja Lune
Leta 1609 sta dva moža, neodvisno eden od drugega, gledala našo Luno skozi nov nizozemski izum – daljnogled ali teleskop, kot so ga poimenovali pozneje. Prvi je bil julija 1609 Thomas Harriot iz Londona, priznani, a nekoliko samotarski matematik in astronom. Nekaj mesecev za njim, je v nebo usmeril daljnogled še Galileo Galilei, petinštiridesetletni profesor matematike na Univerzi v Padovi, ki takrat še ni zaslovel s kakim konkretnim dosežkom. Poučno je primerjati njune osebne zapiske, v katerih imamo zabeleženo, kaj je vsak od njiju mislil, da je opazil, in poskušati razumeti, kje so vzroki za tako velika razhajanja med njima. Seveda sta oba poznala Aristotelovi De Caelo in Metafiziko v katerih piše, da je Luna popolnoma gladka sfera, narejena iz nebesne substance, in simbol nespremenljivega vesolja onkraj Zemlje.
Slika 1. Brezmadežno spočetje, Bartolomé Murillo (1617-1682).
Od srednjega veka naprej je bila Luna na nabožnih slikah znak brezmadežnega spočetja device Marije (glej sliko 1), kar je bilo problematično, saj so se že s prostim očesom nekatera območja Lune zdela temnejša kot druga. Thomas Harriot je pojav poimenoval “tista čudna pegavost“. V Dantejevem Raju mora nebeška Beatrice pomiriti Dantejevo začudenje nad tistimi “prašnimi znamenji” s predavanjem o trenutnem stanju optike. Za razrešitev “pegavosti” je do 17. stoletja nastalo kar nekaj ad hoc teorij, vendar v nobeni nihče ni podvomil o Aristotelovi dogmi o popolni sferičnosti Lune. Med papirji Thomasa Harriota je tudi skica, na kateri je označil mejo med temnimi in osvetljenimi deli Lune (glej sliko 2). Toda Harriot ne pripomni nič o tem, zakaj ta meja ni gladka krivulja, ki bi jo pričakovali na popolni sferi, ampak nazobčana črta. Harriot sicer vidi, vendar mu tedanje domneve otežujejo pot k intelektualni preobrazbi od čutne zaznave k novemu načinu razumevanja.
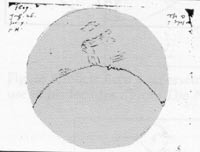
Slika 2. Harriotova prva skica Lune, 1609.
Galilei je v zgodbo vstopil konec novembra 1609. Več tednov je skozi svoj teleskop opazoval Luno, ko je šla ta skozi svoje faze, in to z isto interpretativno veščino, ki jo je kmalu zatem uporabil pri preučevanju Jupitra, Venere, Mlečne ceste in sončnih peg. Tvegano je bilo zaupati novemu instrumentu v tako nabitem kontekstu. Teleskopi kot tudi teorija optike sama so bili zelo primitivni. Leče so imele sferične in barvne aberacije. Nekateri, ki jim je bilo dovoljeno gledati skozi Galileijev teleskop, niso videli tistega, kar je Galilei poskušal pokazati. Filozofi, celo njegov prijatelj Cremonini, pa so tako ali tako mislili, da vsak optični instrument že po svoji naravi popači realnost.
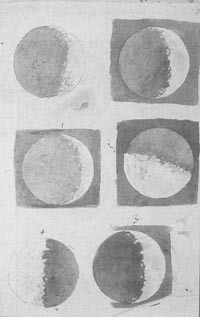
Slika 3. Galileijeve skice s tušem.
Toda Galileijeva samozavest je hitro naraščala. Kot kažejo njegove precizne skice s tušemv chiaroscuro slogu (glej sliko 3), je tudi on videl nazobčano mejo med senco in svetlobo, toda hkrati je bil pozoren tudi na pomemben nov pojav, in sicer na številna svetla območja znotraj temnega dela Lune kot tudi na veliko temnih območij na svetlem delu. Njihov videz se je spreminjal vsake dve do tri ure skupaj s kotom sončne svetlobe. To je Galileija napeljalo na presunljivo misel, da ta mala svetla in temna območja predstavljajo vzpetine in vdolbine, podobno kot gore in doline na Zemlji. “Svetli robovi gora se veličastno dvigajo iz teme.” Površina Lune je bila torej nepravilna, in ne gladka! Iz senc, ki so jo metali vrhovi, je Galilei izračunal, da morajo biti nekatere gore na Luni višje od Alp. Svoja opažanja in razlago zanja je objavil v knjigi Sidereus Nuncius, ki vključuje tudi drzno anti-aristotelijansko pretiravanje (glej sliko 4). 7. januarja 1610 je napisal, da zdaj verjame, da med Zemljo in Luno ni nobene kakovostne razlike. Do 15. januarja je bil že prepričan, da ima Jupiter štiri lune, s čimer je ovrgel aristotelijansko teorijo, da se vsa gibanja v nebesih dogajajo okrog Zemlje.
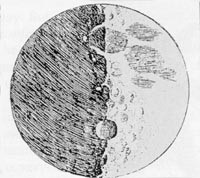
Slika 4. Iz Galileijevega Sidereus Nuncius (1610).
Ko so se Galileijeve senzacionalne ugotovitve razširile po Evropi, so popolnoma spremenile videnja drugih znanstvenikov. Thomas Harriot, ki prej ni zaupal Kopernikovi astronomiji, je spet dvignil svoj teleskop julija 1610. Zdaj ko je prebral Keplerjevo Astronomia nova iz leta 1609 in Galileijevo knjigo iz 1610, je skiciral svoja nova opažanja (glej sliko 5). Zdaj je tudi on videl kraterje in druge lastnosti, podobne tistim na Zemlji, ter celo nekaj takih, ki niso bila objavljena na Galileijevih skicah. Harriot je prepoznal “gorato Luno”. Pomen vizualnih vtisov se je spremenil z novim “razlagalnim vedenjem”, kot je to kasneje poimenoval Martin Kemp.
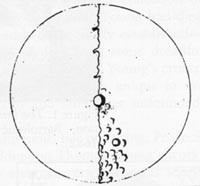
Slika. 5. Harriotova druga skica Lune, 1610.
Oko hodi v šolo: Galilei in renesančna umetnost
Najzanimivejše vprašanje v tej zgodbi je, zakaj sta Galilei in Harriot na začetku tako različno odzvala, čeprav sta proučevala isto Luno. Del odgovora je seveda v tem, da je bil Galilei bolj pripravljen sprejeti Kopernikovo zgradbo vesolja, v katerem so si planeti in sateliti v svojem bistvu podobni, čeprav o njej ni bil popolnoma prepričan do odkritja Jupitrovih lun. Pomemben faktor so tudi Galileijeve izjemne sposobnosti izdelovanja instrumentov ter eksperimentiranja, ki so “gola opazovanja zamenjala z meritvami z rutinskimi postopki pod standardnimi pogoji” (Alan Chalmers).
Velik del Galileijeve prednosti je verjetno prinesel njegovo predhodno urjenje v vizualizaciji. Kot izredno omikan človek, ki je živel v državi, kjer je renesančno slikarstvo prevzelo budne intelektualce, se je Galilei pri petindvajsetih letih prijavil v službo za učitelja geometrije za arhitekte in linearne perspektive za slikarje in kiparje na Academia del Designo. Zelo verjetno je, da je Galilei, tako kot drugi študentje na akademiji, pilil svojo veščino vizualizacije s proučevanjem, kako se trodimenzionalna telesa kažejo očesu in kako mečejo senco pri različni osvetlitvi.

Slika 6. Iz Wetzla Jamnitzerja, Perspectiva corporum regularum (1568).
Slika 6 je primer iz enega popularnih besedil tistega časa, ki prikazuje, kako se vzpetine in vdolbine na mrežastih sferah kažejo na svetlobi in v senci. Strinjam se z znanstveniki, ki trdijo, da je dobro znanje evklidske geometrije Galileiju pozneje pomagalo vplivati na njegovo razumevanje oblik na površini Lune, podobno kot je kasneje neevklidska geometrija podala temelje za sprejetje splošne relativnostne teorije. Galileija je gotovo navduševalo, da je njegovo delo razsvetlilo ne samo znanstvenike, ampak tudi njegove prijatelje humaniste in umetnike, predvsem pa Lodovica Cardija, imenovanega Cigoli, morda najpomembnejšega florentinskega slikarja svojega časa. Ta je v svojem zadnjem večjem delu, freskah v cerkvi Santa Maria Maggiore v Rimu, postavil devico Marijo na galileijsko Luno, ki se je ujemala z ilustracijo iz Sidereus Nuncius (glej sliko 7). Nebesa se niso porušila zaradi napredka znanosti, ampak prej našla način, da le-to vključijo. Pozneje v življenju je Galilei to še drago plačal.

Slika 7. Lodovico Cigoli, Devica brezmadežnega spočetja, 1610-1612.
Naj se za trenutek vrnem k pripombi Marjorie Nicolson, ki pravi, da se modernost začne z Galileijevimi teleskopskimi študijami. Ko se je Galileijev novi pogled na nebesa širil po Evropi, so nekateri že praznovali, saj naj bi ta “ovrgel prejšnjo astronomijo” (Henry Wotton) in z decentralizacijo Zemlje začel tudi novo filozofijo. Druge so te spremembe zelo motile, predvsem njihova implikacija, da je v tem brezkončnem prostranstvu Zemlja morda nepomembna in da morda obstaja mnoštvo drugih vesolij med brezmejnostjo novih zvezd, ki jih je odkril Galileijev teleskop. Te grožnje staremu “redu, razmerjem in enotnosti” (Nicolson) so objokovane v pesmi Johna Donnea iz leta 1611 “Prva obletnica“, ki vsebuje znane vrstice: “In nova filozofija prikliče dvom nad vse, element ognja je ugasnil (...)” in nato “(…) razpadel je nazaj na svoje atome, vse je v koščkih, vsa skladnost je odšla; vse je le dopolnjevanje in razmerje.” Od takrat naprej so se znanstveniki znašli med dvema nasprotnima odzivoma – na eni strani Cigolijev optimizem na drugi pa pesimizem Johna Donnea.
Kako je Einstein izumil splošno relativnost: miselni poskusi
Vendar je bila tako kot v Galileijevih časih vizualna imaginacija vedno odločilna komponenta v mešanici, ki vodi v nove vpoglede. V pismu Jacquesu Hadanardu je Einstein priznal: “Videti je, da besede iz jezika, kot so govorjene ali napisane, ne igrajo nobene vloge v mojem mehanizmu razmišljanja. Fizikalne entitete, ki (tako se zdi) služijo kot elementi v mislih, so zagotovo znaki ali bolj ali manj jasne podobe, ki so lahko prostovoljno reproducirane in kombinirane.” Bilo je, kot bi se v svojem razumu igral z deli sestavljanke. Maxu Wertheimerju je Einstein poročal: “Na sploh zelo poredko razmišljam v besedah. Stvari dojemam z nekakšnim pregledom, nekako vizualno.”
Še več, Einstein, ki je bil predvsem teoretik, in ne eksperimentator, je znal svojo sposobnost vizualizacije uporabiti v svojih domiselnih miselnih poskusih, t.i. Gedanken eksperimente. Pri šestnajstih letih ga je preganjala slika, kako lovi ali jaha žarek svetlobe, za kar je pozneje v svojem življenjepisu dejal, da je vsebovalo seme njegovega poznejšega dela s posebno relativnostjo.
Literatura s področja fizike je polna izrazito vizualnih miselnih poskusov, od Newtonovega poskusa s sodom pa do Maxwellovega demonain mačke v škatli Erwina Schrodigerja. Od vseh teh primerov mi je najbolj pri srcu najpreprostejši. Med dopustom na Institute of Advanced Study v Princetonu sem naletel na kakih dvajset predalov Einsteinovih papirjev in korespondence. Einsteinovo posestvo me je prosilo, da ta zaklad uredim v uporaben arhiv. Med tisoči dokumentov je bil morda najbolj zanimiv še neobjavljen rokopis iz približno leta 1920, v katerem Einstein pripoveduje, kako je izumil splošno relativnostno teorijo. Med obujanjem spominov o svojem poskusu leta 1907, da bi Newtonovo gravitacijo vključil v relativnostno teorijo, piše:
Na tej točki se mi je porodila najsrečnejša misel mojega življenja, in sicer v naslednji obliki: tako kot v primeru polja, ki ga proizvede elektromagnetna indukcija, ima tudi gravitacijsko polje le relativni obstoj. Vzemimo za primer opazovalca pri prostem padu s strehe hiše. Zanj med tem padcem ni nobenega gravitacijskega polja… Če spusti kake predmete (njihove fizikalne in kemijske lastnosti niso pomembne), bodo ti ostali v stanju mirovanja glede nanj. Opazovalec torej upravičeno smatra svoje stanje kot “mirovanje”. (Podčrtano v izvirniku.)
Ta izmišljeni prizor vsebuje ključ do dejstva, da lahko učinke pospešenega gibanja in gravitacije štejemo za enake. Tu je Einstein končno našel, kar je sam imenoval “mogočni argument, da postulat posebne relativnosti lahko razširimo” na splošno relativnost.
Odpoved predstavam o svetu: kvantna mehanika
Primere o moči, ki jo ima vizualizacija v fazi rojevanja znanstvenih odkritij, lahko vedno znova najdemo v delih drugih umetnikov znanosti, kot sta Faraday in Rutherford. Ko je Niels Bohr prevzel podobo planetarnega sistema za svoj model atoma leta 1913, je bilo to pravo odkritje, in Bohr sam je bil navdušen, da je v svojih predavanjih pooblastil in uporabljal barvite predstavitve številnih atomov (na sliki 8, na primer).
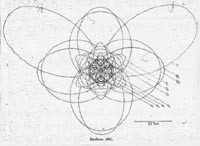
Slika 8. Bohrova ponazoritev atoma radija, pripravljena za uporabo med njegovimi predavanji. (Iz Die Naturwissenschaften, 6. julij 1923.)
Vendar je do srede dvajsetih tega stoletja postalo jasno, da je nevarno nadaljevati z razmišljanjem o atomskih procesih na način, ki uporablja podobe, izumljene za večje dogodke, na primer, gibanje planetov. Potrebni so bili novi načini zamišljanja pojavov, kot so spin elektrona ali svetlobe kot vala in delca hkrati. Intuicije, ki so se zlahka vizualizirale, so postale ovira za napredek. Ni nam treba vedeti veliko o načelu nedoločenosti Wernerja Heisenberga, da vidimo, da natančno zarisane orbite v Bohrovem modelu atoma v naravi ne morejo obstajati. To je Heisenberga vodilo, da je od sredine dvajsetih let naprej predlagal nujno, a drastično rešitev, tako, ki danes otežuje laiku, da bi se počutil doma v svetu sodobne fizike. Heisenberg je popolnoma izločil uporabo slikovnih modelov atoma. Tipični Heisenbergov dictum je trdil: “Program kvantne mehanike se mora najprej osvoboditi teh intuitivnih slik. Nova teorija se mora predvsem popolnoma odpovedati vizualizaciji.” Stari Anschaulichkeit je moral stran.
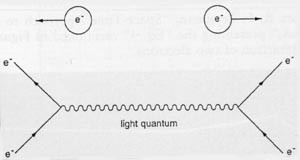
Slika 9. Zgornji del: “klasična” ponazoritev elektronov, ki se odbijajo eden od drugega. Spodnji del: vzajemno sipanje istih elektronov, predstavljenih v prostoru-času, ki medsebojno učinkujeta z izmenjavo (navideznega) svetlobnega kvanta. (Iz A. I. Miller, Imagery of Scientific Thought [ Boston: Birkhä user, 1984] , 257.)
V večini drugih vej znanosti je danes še vedno živa ikonska domišljija. Toda kvantni znanstveniki so morali najti nov način vizualizacije, tak, ki temelji bolj na matematičnih, in ne fizikalnih konstruktih, na primer abstraktni diagrami, ki jih lahko povežemo z izrazi v matematičnih enačbah. Slika 9 vsaj nakazuje ta nov način. Zgornji del slike je znana ilustracija iz učbenikov, ki na zelo plastičen način prikazuje, kako enako nabita delca delujeta drug na drugega. To je nekakšna trenutna slika situacije v prostoru, kjer odbojne sile delujejo čez vrzel med delci, da bi se ti sipali eden od drugega. Toda veliko bolj smiselno je razmišljati o takšnem pojavu, ki se dogaja v prostoru-času, povzroča pa ga vzajemno izmenjavanje namišljenega fotona, nekakšnega sla, ki posreduje pri interakciji med dvema nabitima delcema. Spodnji del slike prikazuje ta novi način na diagramu, imenovanem po svojem predlagatelju, Richardu Feynmanu. V enem svojih zgodnjih člankov (1949) je predstavil svojo novo vizualizacijo sipanja: vsak krak v diagramu prostora-časa na sliki 10 ustreza vsaj kvalitativno delu enačbe, ki nadrobno opisuje pojav (glej sliko 11).
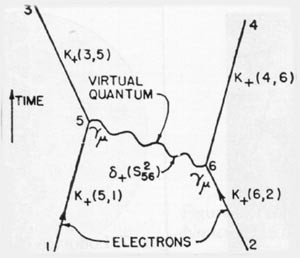
Slika 10. Iz članka R. P. Feynmana, Space-Time Approach to Quantum Electrodynamics, Physical Review 76 (1949): 772. Feynmanov povzetek pravi: “Osnovna enačba interakcije (4). Izmenjava enega delca med dvema elektronoma.” In dejansko je diagram vsaj kvalitativna vizualna ponazoritev sipanja dveh elektronov, pojava, ki ga natančno opisuje enačba na sliki št. 11.
Prelomljena črta od točke 1 do točke 3 na sliki 10 predstavlja gibanje elektrona na levi v prostoru in času. Podobno črta od 2 do 4 predstavlja pot elektrona na desni v istem časovnem intervalu. Delca se najprej približujeta in nato odbijeta. Interakcija med njima, ki spremeni njune poti, je prikazana z absorpcijo navideznega kvanta na levi (točka 5), ki ga je malo prej oddal delec na desni (točka 6). Vendar si lahko, kot pravi Feynman, to interakcijo mislimo tudi kot emisijo navideznega kvanta v točki 5 na levi in njegovo absorbcijo ob zgodnejšem času v točki 6 na desni.

Slika 11. Iz članka R. P. Feynmana, Space-Time Approach to Quantum Electrodynamics, predstavitev “enačbe 4”, omenjene na sliki št. 10, ki vlada interakciji dveh elektronov.
Kot je Silvan S. Schweber zapisal v svoji novi knjigi, QED, je bil en element Feymanovega genija njegova izostrena moč vizualizacije. V nekem intervjuju je Feynman dejal: “Ves čas vidim slike povezane s tistim, kar poskušam narediti.” Toda skromno je dodal: “Diagram je v resnici v nekem smislu slika, ki nastane pri poskusu, da bi si razjasnil vizualizacijo, ki je nekakšna na pol pečena ohlapna stvar, pomešana s simboli. Težko jo je razložiti, saj ni jasna.” Vendar je kljub temu bila dovolj jasna, da je postala standardno orodje razuma generacij fizikov, ki so sledile. V vsakem primeru, kot je rekel tudi Feynman, “na koncu prevzame stvari matematika, in ta je lahko učinkovitejša od slike.”
Atom kot sončni sistem: analogije v fiziki
Zdaj se moram, čeprav bolj na kratko, vrniti k drugim pomagalom domišljije. Eno je uporaba analogije. To vas morda preseneča, saj nas filozofi že dolgo svarijo, da ta tehnika razmišljanja ne more imeti kakega dobrega namena v znanosti. Slovar sodobne misli (The Dictionary of Modern Thought) pravi, da je analogija “oblika razmišljanja, ki je še posebej nagnjena k temu, da iz resničnih postavk sklepa napačno“. In res, analogija in njena bližnja sorodnica metafora veljata za osnovo poezije. Delujeta skozi iluzijo in gotovo je znanstvenikova obrt popolno nasprotje temu. A še vedno se ti orodji z lahkim srcem na veliko uporabljata, pogosto zelo uspešno in neodvisno od obširne literature na temo metafore in analogije v literarni kritiki in filozofiji.
Videli smo že, kako analogije delujejo v praksi: ko je Galilei primerjal strukture na Luni z Alpami na Zemlji, ko si je Bohr sposodil sončni sistem za svoj atom, ko je Einsteina obšla tista srečna misel, da ima gravitacijsko polje le “relativni obstoj” na isti način kot električno polje. Da si nevidni svet lahko predstavljamo in govorimo o njem, ga moramo skoraj nujno naseliti z antropomorfnimi in vsakdanjimi koncepti. Pomislite samo na Mendelejeve družine elementov; na Rutherfordove in Soddyjeve dolge verige starševskih in hčerinskih nukleidov pri razpadu atomov, vsakega s svojim življenjem ali (bolje) najmanj pol življenja; na sami besedi “val” in “delec” pri subatomskih pojavih; na koncepte, kot je toplotni ali električni tok; na črte sil v polju; na vse tiste metafore, še posebej v vojski in medicini – invazija, napad, obramba – in drugje v znanosti, na primer Darwinovo drevo življenja in (pred tem) Newtonove centre privlačnosti, njegov urni mehanizem vesolja itn. (Kot je Aristotel dejal v Poetiki: “Toda daleč največji dosežek je biti mojster metafore. To je stvar, ki se je ne moremo naučiti od drugih; je tudi znak genija, saj dobra metafora zahteva intuitivno dojemanje podobnosti med različnostmi.”)
Veliki mojster med analogisti je bil Enrico Fermi. V začetku leta 1934 je z Emiliom Segrejem in Edoardom Amaldijem raziskoval učinketlakana spektre alkalov. Kot je kasneje dejal Amaldi, “da bi razložili dobljeni učinek, je Fermi izdelal teorijo o trku zelo počasnega elektrona z atomom. Ta ista teorija je bila leto in pol pozneje uporabljena za trke počasnih nevtronov z jedri“, poskus, ki je temeljni kamen atomske dobe. Velik korak je bil tudi uvid Lise Meitner in Otta Frischa konec leta 1938 med njunim božičnim izletom v zasneženo pokrajino, ko sta bila v izgnanstvu. Vedela sta za model Georga Gamowa, ki je imel atomska jedra za analogna kapljicam tekočine, in si vizualno predstavljala, kako bi lahko “kapljica” jedra urana doživela tako močne oscilacije, da bi razpadla. Na ta način je bila prvič priznana možnost fizije, Meitnerjeva in Frisch pa sta na priznanje čakala več desetletij.
Barve svetlobe kot zvoki piščali: primer genialnega uvida
Moj najljubši dokaz za uporabnost razmišljanja s pomočjo analogije najdemo v delu Thomasa Younga, fizika iz 19. stoletja. Slavo si je v glavnem pridobil z razvojem zamisli, da je svetloba pojav pri valovanju, kar je bilo v nasprotju s kvazi-delčno teorijo svetlobe, ki so jo povezovali z Newtonom in je bila takrat izjemno priljubljena. V enem svojih prvih člankov (leta 1800), Thomas Young, takrat star 27 let, piše: “Svetloba je širjenje impulza, ki ga v eter oddajajo svetlobna telesa.” Bralca opomni, da “je že Euler domneval, da barve svetlobe sestojijo iz različnih frekvenc vibracij svetlobnega etra“. Do takrat je bilo to le ugibanje, in ne le ena od ugotovitev v newtonovskem načinu razmišljanja. Toda zdaj Thomas Young trdi, da ima namesto domneve potrditev: Ideja, da je svetloba širjenje impulza v etru, “je močno potrjena“. S čim? Kako? “Z analogijo med barvami tanke plošče in zvoki piščali” – dveh zelo različnih stvari. Ne da bi se sploh poglabljali v študij podrobnosti te presenetljive in, kot se je izkazalo, izredno plodovite analogije med svetlobo in zvokom, občutimo izredno drznost tega prenosa pomena. In res, pogum za to povezavo se je zdel tako nepriporočljiv, da je celo George Peacock, Youngov vdani prijatelj, matematik in profesor na univerzi v Cambridgeu, ki je leta 1855 uredil in izdal zbirko Youngovih člankov, 26 let po Youngovi smrti in dolgo po tem, ko se je valovna teorija že uveljavila, še vedno čutil, da mora svoje bralce rešiti pred težko napako glede te točke. Zato je Youngovemu bistvenemu stavku dodal zvezdico in ga opremil z ostro opombo, morda edinstveno v literaturi: “Ta analogija je plod domišljije brez prave osnove. Opomba urednika.”
Jasno je, da se svetloba in zvok razlikujeta. Peacock je seveda vedel, da sta Arago in Fresnel, ki sta se opirala na Youngovo delo, določila, da je svetlobno valovanje transverzalno, medtem ko je valovanje zvoka v orglah longitudinalno. Peacock je v tej analogiji videl le razlike, in ne podobnosti. Toda Youngov vpogled je bil nekaj genialnega. Barve tanke plošče, ali, če hočete, milnega mehurčka in oljnega madeža, so odvisne od debeline plasti, prav tako kot je zvok, ki ga proizvajajo piščali, odvisen od njihove dolžine; to je bilo ključno dejstvo, da sta oba, svetloba in zvok in torej barva in višina rezultat lastnosti valovanja, natančneje valovne interference. Peacockova opomba urednika bi se morala glasiti: S to rodovitno analogijo je Young stopil v anale zgodovine, čeprav je kampanja njegovih nasprotnikov, britanskih newtonovcev, kmalu poskrbela za konec njegove kariere produktivnega znanstvenika.
Predsodek kot vir navdiha: tematska imaginacija
Na koncu preletimo še tretje od orodij, ki lahko spodbudijo začetne faze raziskav. Ta vidik sem poimenoval tematska domišljija. S temo (iz grške besede thema – to, kar je podano s propozicijo) mislim na pogosto neizpričane ali celo podzavestne osnovne predpostavke, preference in vnaprejšnje koncepte, ki jih znanstveniki lahko vzamejo za svoje, tudi če jih podatki aktualne teorije ne vodijo k njim. Ta strategija je seveda v nasprotju z vsakim dobrim nasvetom, od opozorila Francisa Bacona pred štirimi idoli do vztrajanja Karla Poppra pri poskusu ovrženja in današnjih priročnikov pravilnega ravnanja. In res, zvestoba svoji temi lahko vodi v propad, kot je Darwinov buldog, T. H. Huxley, opozarjal že pred stotimi leti: “Zdi se mi, da znanost uči na najvišji in najmočnejši način veliko resnico, ki je utelešena v krščanskem dojemanju popolne predaje božji volji. Sedi pred dejstvom kot majhen otrok, bodi pripravljen opustiti vsakršen predsodek, ponižno sledi kamorkoli in v kakršnakoli brezna te vodi narava, ali pa se ne boš naučil ničesar.”
Veliko je primerov, ko je znanstvenik dosegel uspeh pri tem, da se je za nekaj časa goreče oklepal svoje najljubše teme, tudi ko je na začetku obstajal očitno protisloven dokaz. Tu govorimo o znanstvenikovem zavestnem zavračanju dvoma, analognem temu, kar je Samuel Taylor Coleridge videl kot nalogo pesnika, in ne daleč od tistega, za kar je John Keats uporabljal izraz “negativna sposobnost” velikih avtorjev (njihova sposobnost “ostati zadovoljen s polovičnim znanjem“).
Tematski profil znanstvenika se pojavi, ko preučujemo njegove zgodnje osnutke, zapiske iz laboratorija, pisma in objave. Einsteinove trdne a priori preference so, na primer, raje vključevale združitev ločenih delov teorije fizike (Steven Weinberg je podobno govoril o “Newtonovih sanjah razumeti vso naravo“), invarianco, simetrijo, popolnost opisa in v svojem bistvu newtonovsko vzročno povezanost dogodkov kot pa temeljno naključnost (od tu njegovo globoko nestrinjanje s Niels Bohrovim pogledom na fiziko). Einstein je svoje predpostavke imenoval svobodno izbrane “kategorije” in v tem pogledu so se razlikovale od kategorij Immanuela Kanta, ki so bile “nespremenljive in pogojene z naravo razumevanja“. Einstein je gladko zavrnil napade na svoje predpostavke s pripombo, da bi zanj razmišljanje brez njih “bilo nemogoče, kot je nemogoče dihanje v vakumu“. Čeprav teme lahko motivirajo in dajo navdih raziskavi, morajona koncu prestati test izkušnje in biti ocenjene glede na to, koliko pomagajo narediti svet pojavov “razumljivejši”. Narave ne moremo imeti za norca. Tako lahko rečemo, da so Einsteinu njegove tematske izbire odlično služile v zgodnjih desetletjih. V njegovih zadnjih letih pa je bilo njegovo zagrizeno iskanje združene teorije polja znotraj lastnih predpostavk le težko oranje ledine.
Teoretične postavke koncepta teme sem na široko razvil še v drugih člankih, zato bom tu prikazal le dva primera njegovega praktičnega pomena.
Grotesknost atomskega sveta: solvayska konferenca
Konec 19. stoletja so fiziki še vedno lahko verjeli, tako kot Newton, da naravni pojavi v svojem bistvu ne skačejo, da niso nezvezni. Od leta 1900 naprej sta Planck in Einstein čutila, da morata, čeprav nerada, vpeljati koncepte kvantnih skokov energije na ravni atoma in nezvezne kvante svetlobne energije, pozneje imenovane fotoni. Ali je ta “temeljna nezveznost ali raje individualnost” atomskih procesov, kot jo je poimenoval Bohr (1927), res nujna, je postala glavna tema srečanja leta 1911, ki mu ni primere. Večina velikih svetovnih fizikov se je zbrala v sobi v Bruslju (na tako imenovani prvi solvayski konferenci). Kot se redko zgodi, je tu prišel na dan tisti strastni del intelektualnega življenja znanstvenikov. Walther Nerst, organizator konference, je dejal, da je kvantna fizika na dnu “zelo čudno, groteskno pravilo“. Max Planck je pozneje zapisal: “Kar se mene tiče, sovražim nezveznost…” Henri Poincare pa je po vrnitvi s konference vzkliknil: “Hipoteza gospoda Plancka je tako čudna, da ji moramo ubežati na kakršenkoli možen način. Zaenkrat ga še nismo našli. Je nezveznosti usojeno vladati fizikalnemu vesolju in ali je njena zmaga dokončna?“ Prej je izjavil, da bi bila brez hipoteze o zveznosti “celotna znanost nemogoča“.
In vendar je nezveznost na koncu razlagalne verige zmagala z odkritjem Ernesta Rutherforda leta 1911, da atom, ki je vse nekaj drugega kot želatinast predmet, vsebuje majhno trdo jedro. Spet so tristo let po letu 1611 nekateri umetniki mislili, da je samo strukturo vesolja prizadel potres. Tako je slikar Wassily Kandinsky o tej dobi napisal: “Kolaps modela atoma je v moji duši enak kolapsu celotnega sveta. Kar naenkrat so se porušile najdebelejše stene… znanost se mi je zdela uničena.” Zgodovinarje kulture so dolgo mučili ti nelogični in analogni preskoki čustev in domišljije onstran znanosti, istočasno na več frontah. Treba je samo omeniti učinek baletov Stravinskega (Firebird 1910, Petrouchka 1911, Rite of Spring 1912), Armory Show leta 1913 in postimpresionistično razstavo Rogerja Fryja v Londonu 1910, enega od razlogov za opazko Virginije Woolf, ki je postavila datum nove modernosti: “Približno decembra 1910 se je človeški značaj spremenil…“
Začudenje in vznemirjenje: Wilsonove fotografije atomov
Vsekakor pa so se fiziki dokaj hitro sprijaznili z nezveznostjo narave pri atomskih pojavih, delno zato, ker je leta 1912 britanski fizik C. T. R. Wilson prvi predstavil vidne znake za submikroskopska dogajanja, in sicer s pomočjo dramatičnih fotografij, posnetih s svojim novim izumom, meglično celico. Slika 12, na primer, prikazuje sled kondenzacije – tanko črto megle, ki ostane na poti alfa delca, ki se je odcepil iz radija. Kot je dejal Wilson, je sled “še posebej zanimiva” zaradi svojih “dveh absolutno nenadnih zavojev“. Tu je dokaz za nezveznost: alfa delec se ostro odkloni po trčenju v težko jedro plina, ki napolnjuje celico. In pravzaprav je drobna sled na prvem odklonu tista, ki izostrenemu očesu pokaže odmik nesrečnega jedra po trku.

Slika 12. Ena izmed zgodnejših fotografij iz meglične celice C. T. R. Wilsona, ki nakazuje pot alfa delca in njegove “nenadne zavoje”. (Iz Proc. Roy Soc. London [ A] 87 [ 1912] : 277.)
Take slike so nato postale vzrok zanimivih razhajanj med filozofi glede odnosa med opazovanim in realnostjo. Toda za večino znanstvenikov, ki so po navadi pragmatični realisti, so bile odločilne. Robert A. Millikan je poročal, da so te fotografije, ko so bile prvič predstavljene na znanstvenem srečanju leta 1912, svoje opazovalce napolnile “z začudenjem in vznemirjenjem (…) vznemirjenjem ob popolni vidljivosti” samega procesa. Kar bi John Donne spet lahko poimenoval “nova filozofija”, je zavladalo skupaj z novo temo nezveznosti in razpada njegovih “atomov”. V Ameriki je vse to že predvidel Henry Adams, ki je leta 1905 v Education zapisal, da bo novo stoletje videlo stare enote, kako razpadejo v mnogoterost.
Millikanove “goljufije”: merjenje naboja elektrona
Moj drugi in zadnji primer tematske komponente znanstvene misli prihaja iz enega mojih najljubših primerov, kjer se zgodovinarju vztrajna zvestoba predpostavki odkriva pri gledanju skozi ključavnico laboratorijskih vrat. V tistih vznemirljivih letih, 1911 in 1912, se je Millikan, takrat še precej neznan fizik na mladi Univerzi v Chichagu, odločil, da bo natančno izmeril naboj elektrona, osnovne konstante v naravi, katere vrednost je bila takrat še zelo vprašljiva. Niti za trenutek ni dvomil, da vsi elektroni nosijo natančno enako diskretno količino naboja (ponavadi simbolno zapisano s črko e), na enak način, kot se je smatralo, da imajo vsi atomi istega elementa enako maso. Millikan je bil dolgo “precej prepričan” v to svojo idejo predvsem, ker je njegov osebni junak, ki mu je pravil “naš lastni Benjamin Franklin”, leta 1750 dejal, da ima vsa elektrika zrnato strukturo, kjer vsako zrno, kot je to parafraziral Millikan, sestoji iz “električnega delca ali atoma“.
Čez nekaj trenutkov bomo videli, kako je ta ideja določila, kaj je delal Millikan v svojem laboratoriju. Vendar se najprej spomnimo, da je na koncu le dobil presenetljivo dobro vrednost za e, kar je bilo navedeno tudi kot del utemeljitve za podelitev Nobelove nagrade, ki jo je leta 1923. Toda v tistem času je poleg njegove slike diskretnosti obstajalo tudi alternativno gledanje. Felix Ehrenhaft iz stare dunajske univerze, ki je bil pod velikim vplivom antiatomizma Ernsta Macha, je bil prepričan, da je bila izmerjena vrednost e le poprečje, dejanski naboji različnih elektronov pa so se spreminjali od skrajno majhnih subelektronov do veliko večjih vrednosti. Imel je tudi svoje lastne poskusne meritve, ki naj bi to potrjevale (čeprav se je pozneje izkazalo, da je uporabljal popolnoma neprimerno metodo, samo da bi si zagotovil variabilnost, ki jo je iskal).
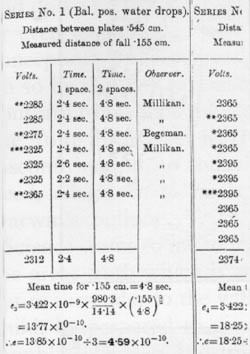
Slika 13. Tabela podatkov iz enega Millikanovih prvih pomembnješih člankov o naboju elektrona. (Iz Philosophical Magazine 19 [ 1910] .)
Zdaj se je Millikan znašel sredi tekme med zaslugami dveh nasprotujočih si tem, kar ni v zgodovini znanosti nič nenavadnega. Millikanova tabela podatkov (slika 13) iz enega njegovih zgodnjih člankov nas opozarja na njegovo pripravljenost, da bi prevzel veliko tveganje v službi ideje, tveganje vsaj za naše sedanje standarde, ki pa jih ne smemo prehitro preslikati v preteklost. Millikan je opazoval obnašanje nabitih kapljic in veliko ponovitev označil z zvezdico. V svojem članku razlaga: “Opazovanja označena s tremi zvezdicami imajo v moji beležki oceno ‘odlično’.” Dve zvezdici pomenita “zelo dobro”, ena zvezdica “dobro”, druge pa le “še kar”, sedem opazovanj pa je bilo “izločenih” kot “negotovih”. Na tej točki obstaja šest takih tabel za celo serijo poskusov, ki jih na koncu zbere skupaj, da bi določil najboljšo vrednost za e. Za obdelavo podatkov še ni uporabljal statistike. A vseeno je bil končni rezultat, e = 4,65*10-10 esu, zelo dober za tisti čas in ga je Niels Bohr takoj uporabil za svoje delo na modelu atoma. Na misel mi pride šaljiva besedna zveza, ki jo je skoval H. C. Oersted, fizik iz 19. stoletja. Oersted je dejal, da so nekateri znanstveniki sposobni “vnaprejšnjega sozvočja z naravo“.
V naslednjih dveh letih je Millikan zelo izboljšal svojo napravo za opazovanje gibanja oljnih kapljic v električnem in gravitacijskem polju. Avgusta 1913 je objavil svoj klasični in dokončni članek. V njem podaja podatke, ki jih je dobil z poskusi na 58 ločenih oljnih kapljicah, ter za e dobi vrednost 4.774*10-10 esu z relativno napako ena proti tisoč. Tega rezultata ni bilo moč izboljšati dve desetletji.
V Millikanovem arhivu sem našel laboratorijske beležke njegovega dela. Lahko jih uporabimo, da pokukamo v njegov laboratorij in vidimo, kako mu je njegovo tematsko prepričanje, da obstaja edinstvena in diskretna vrednost za e, pomagalo izbirati med podatki. 58 ponovitev poskusa, ki jih je objavil, se nanaša natančno na ustrezne vnose podatkov, toda znašajo le 40 odstotkov celotnega števila kapljic, ki jih je dejansko pregledal, ostalih kapljic zabeleženih v njegovih zapiskih pa ne uporabi. Njegovo zavestno zavračanje dvoma glede nasprotujočih si podatkov je jasen. Ehrenhaft bi najbrž bil presrečen, če bi imel dostop do podatkov v teh beležkah, ki niso prišli v Millikanov članek.
Da bi bil lahko prepričan o pravilnem izvajanju poskusa, še posebej, ko dela z na novo izumljeno opremo, mora do danes vsak eksperimentator imeti občutek, kako zunanje okoliščine, v tem primeru nihanje napetosti, temperaturne spremembe, turbulenca v celici, vplivajo na predpostavke, na katerih je zgrajen poskus. Galilei je imel podobne probleme s svojim novim teleskopom. Današnje strategije za obdelavo protislovnih podatkov so popolnoma drugačne in v luči teh strožjih pravil nas kaj lahko zanese, da obtožujemo Millikana prevare. Ta diskusija pa vodi k pomembni temi, v katero se na tem mestu ne bi spuščal.
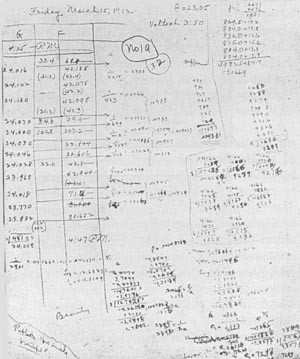
Slika 14. Podatki in izračuni v Millikanovem zvezku, 15. marec 1912.
Raje dajmo priznanje navdušenju, ko gredo stvari dobro, ki si ga je Johannes Kepler lahko dovolil deliti z javnostjo, na splošno pa so ga znanstveniki pred njo raje skrivali. Slika 14 prikazuje podatke in izračune tipične za eno “dobrih” ponovitev poskusa; v spodnji levi kot strani Millikan zapiše: “Lepota. To zagotovo objavi, lepo!” (Glej sliko 15.) In podobno stran za stranjo, na primer, na sliki 16: “Objavi. Lepota v vsakem pogledu… Skoraj idealno.”

Slika 15. Podrobnosti slike št. 14.

Slika 16.

Slika 17. “e = 4.98 + [ predaleč] , kar pomeni, da to ni mogla biti kapljica olja.” Millikan je delal z oljnimi kapljicami dovolj dolgo, da je znal prepoznati vsiljivca, na primer prašni delec, obdan s plastjo olja.
Toda v primerih, ko so oljne kapljice težke in se gibljejo prehitro, ali ko ima Millikan kakšne druge dvome, se njegovo navdušenje poleže, na primer, “nekaj narobe“, “ne ustreza“, “velika napaka, ne bom uporabil“. In te kapljice res ne pridejo v članek (za najbolj osupljiv primer glej sliko 17). Gledano z Millikanovega stališča to niti niso bile zgrešene ponovitve. To sploh niso bile ponovitve. Namesto da bi zgubljal čas z iskanjem krivca za težave, kot bi to seveda lahko naredil, je preprosto nadaljeval z naslednjo množico preučevanj druge kapljice. V rokah koga drugega bi se to lahko slabo končalo. Tokrat mu je njegova tematska izbira pomagala k uspehu. Toda svoj naslednji projekt, raziskava fotoelektričnega učinka, je začel z napačnimi predpostavkami. Trmasto je deset let vztrajal pri delu in na koncu nerad opustil svojo priljubljeno predpostavko, kar je vodilo k drugi polovici njegove Nobelove nagrade. A brez svojih predpostavk, ki so ga visoko motivirale, morda sploh ne bi vedel, kako začeti in kje biti bolj strog, tako v prvem kot v drugem primeru.
Neracionalni um genijev: vhod v skriti red stvari
Tri oblike osebne umetnosti znanstvene domišljije, ki sem jih opisal danes, lahko pomagajo preseči idejo znanosti kot stroja in brezstrastnega procesa indukcije iz dejstev, o katerih ne dvomimo. Spet pa ne bi bilo prav zanemariti vedno prisotne, komplementarne množice veščin – logično razmišljanje, obrt in druga strokovna znanja, ki se jih je treba naučiti in ki jih lahko delimo. Zatreti le-te bi pomenilo pustiti atenske spomenike nezaščitene, da jih glasne špartanske vrane lahko raztrgajo.
Ob koncu pa še opozorilna opomba. Jasno je, da Galileija ali Marie Curie ne moremo bolj “razložiti” od Danteja ali Mozarta. Periklej je padle vojake v Peloponeških vojnah hvalil, ker so svoja dejanja položili “ob vznožje svojega mesta kot najveličastnejši prispevek, kar so ga lahko ponudili“. Nekaj takega so na svoj način naredili tudi znanstveniki, nekateri z velikimi osebnimi žrtvami. Kako človeški razum najde vhod v skrit red stvari, kako nekateri odprejo popolnoma nove svetove in odkrijejo namige temeljnih zakonov narave – to pa lahko samo poskušamo osvetliti, čeprav ne bomo nikoli popolnoma razumeli. Tu predajam zadnjo besedo spet Einsteinu. “Tu,” je rekel, “leži smisel za čudež, ki se še povečuje – natančno tako, kot narašča razvoj znanja.”
(prevedla Tatjana Marvin)
kvarkadabra.net – številka 3 (februar 2000)
















